3 Операції над відношеннями

Повернимося до наведеного раніше відношення, яке назвемо «Батько».

Якщо упорядкована пара елементів (х, у) визначає факт, що х – є батьком у, то у – є дитиною х. То ж з цього виходить, що крім відношення «Батько» існує ще відношення «Дитина», якому належить пара (у, х). Очевидно, що граф відношення «Дитина» можна отримати, помінявши в графї «Батько» напрямки дуг:

Цей приклад пояснює поняття оберненого відношення.

Нехай R-бінарне відношення. Обернене відношення до R позначається R^-1. Упорядкована пара (у, х) R^-1 тоді і тільки тоді, коли (х, у) ) R.

Я кщо R  X², то R^-1 X², де Х – деяка множина. Якщо R  X  Y, то R^-1 Y  X.

Я кщо бінарне відношення задане на 2-х множинах, то граф відношення можна побудувати таким чином. Вершини графа, що відповідають елементам першої множини розташуємо ліворуч, вершини, що відповідають елементам другої множини – праворуч. Нехай задані множини: A = {a, b, c, d, e, f}, B = {1, 2, 3, 4} і відношення R = {(a,1), (a,2), (b,4), (d,1), (f,4)}.

Тепер вивчимо спосіб одержання відношення з двох відношень, використовуючи операцію композиції.

Нехай задані множини: A = {a, b, c, d, e, f}, B = {1, 2, 3, 4} і відношення R = {(a,1), (a,2), (b,4), (d,1), (f,4)}. Ще визначимо множину С = {w, x, y, z} і відношення S = {(1,x), (2,y), (3,x). (3,z)}, S B  C.

Н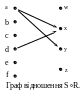 ехай R і S – відношення, такі, що R  X  Y, S Y  Z, де X, Y, Z – деякі множини. Композицією відношень R і S називається відношення, що складається з упорядкованих (x,z), xX, zZ, для яких існує елемент yY, такий, що виконуються умови (x,y)R, (y,z)S. Композиція відношень R і S позначається S∘R.

Зокрема, для відношень R  А  В і S B  C композиція S∘R є відношення зображене на малюнку і є підмножиною декартового добутку А  C.

Операція композиції відношень дозволяє ввести поняття бінарного відношення, що задане на одній множині.

Нехай R – деяке відношення, визначене на множині X: R X  X. Тоді n-ий степінь відношення R позначається R² і визначається рекурсивно так:

R⁰ – тотожне відношення на множині Х;

Rⁿ = R^n-1∘R.

Із визначення маємо, що R² = R∘R, R³ = R²∘R.

Приклад. Нехай відношення R на множині A = {a, b, c, d} задане графом:

Розглянемо ще одну операцію, яка називається перерізом бінарного відношення.

Нехай R  X  Y – відношення на множинах X і Y. Якщо xX, то перерізом відношення R за х (позначається R(x)) є множина R(x)  Y, що складається з елементів yY, таких, що (х, у)  R.

Об’єднання перерізів за елементами деякої множини Z X називається перерізом R(Z) відносно підмножини Z.

Множина, що складається з перерізів відношення R X  Y за кожним елементом з Х, називається фактор-множиною множини Y за відношенням R і позначається Y/R. Формально можна записати, що Y/R = {R(x), хX}.

Приклад. Розглянемо перерізи відношення R на множинах A = {a, b, c, d, e, f}, B = {1, 2, 3, 4}, R = {(a,1), (a,2), (b,4), (d,1), (f,4)}.

Перерізи : R(a)={1,2}, R(b)={4}, R(c)=, R(d)={1}, R(e)= , R(f)={4}.

Фактор-множина B/R={{1,2}, {4}, {1}, }.

Розглянемо множину D = {d, e, f}, D A. Переріз відношення R за множиною D виглядає таким чином: R(D)=R(d)R(e)R(f)={{1}, {4}, }.

Крім наведених операцій до відношень застосовані множинні операції об’єднання, перетин, різниця та доповнення. Розглянемо два відношення R  X  Y і S  X  Y. В результаті операцій RS, RS, R\ S одержимо множини упорядкованих пар, що є відповідно об’єднанням, перетином, різницею множин R і S.

Запитання.

1. Що називається оберненим відношенням і як воно позначається?

2. Як отримати граф відношення, оберненого до даного?

3. Що називається композицією відношень?

4. Нехай R – деяке відношення. Що означає запис R² , R³ ?

5. Дайте визначення перерізу відношення R і фактор-множини за відношенням R.

6. Назвіть операції, які застосовуються до відношень.

 Завдання.

1. Нехай R₁ і R₂– бінарні відношення на множині А ={a, b, c, d} , де R₁={(a,a), (a,b), (b,d)}; R₂={(a,d),(b,c),(b,d),(c,d)}:

   1. побудуйте відношення, R₂∘R₁, R₁², R₂³;

   2. побудуйте перерізи відношень R₁, R₂ за елементами a, d і відносно підмножини {a, b};

   3. побудуйте фактор-множину за відношенням R₂.

2. Знайдіть відношення R^-1, якщо відношення R задане таким чином:

   1. (a,b)R a, bN, a>b;

   2. (a,b)R a, bN, a – дільник b;

   3. А – множина країн світу; (a,b)  R, якщо a,b А і країна a межує з b.

3. Нехай А ={1, 2, 3}, В ={1, 2, 3, 4} і відношення R₁, R₂ AB:

R₁={(1,2), (2,3), (3,4)}; R₂={(1,1),(1,2),(2,2),(2,3) ),(3,1) ),(3,2) ),(3,3) ),(3,4d)}.

1. R₁R₂;

2. R₁R₂;

3. R₁\R₂;

4. R₂\R₁;

4. Нехай А – множина студентів технікуму, В – множина книг в бібліотеці. Нехай задані відношення R₁, R₂: R₁ AB, такі, що (a,b)  R₁, якщо студент а згідно з навчальною програмою повинен під час навчання прочитати книгу b, і R₂ AB, такі, що (a,b)  R₂, якщо студент а вже прочитав книгу b. Дайте словесний опис відношень, що одержуються в результаті виконання операцій:

1. R₁R₂;

2. R₁R₂;

3. R₁\R₂;

7