- •§17 Понятие геометрического преобразования плоскости. Группа геометрических преобразований. Групповой подход к классификации геометрий.
- •§18 Движения. Их свойства. Основная теорема о движениях. Движения первого и второго рода.
- •§19 Движения первого и второго рода. Теорема о задании движения, род которого известен.
- •§20 Параллельный перенос.
- •§21 Поворот.
- •§22 Центральная симметрия.
- •§23 Осевая симметрия.
- •§24 Скользящая симметрия.
- •§25 Классификация движений плоскости (теорема Шаля).
- •§26 Признаки движений.
- •§27 Гомотетия и ее свойства.
- •§28 Подобие.
- •§29 Аффинные преобразования. Предмет аффинной геометрии.
Геометрические преобразования плоскости
§17 Понятие геометрического преобразования плоскости. Группа геометрических преобразований. Групповой подход к классификации геометрий.
Геометрические преобразования плоскости (ГПП) имеют важное значение в науке и в методике. Значимость в научном плане определяется тем, что они лежат в основе классификации геометрий, а именно: каждой группе ГПП соответствует своя геометрия. Так, например, элементарная геометрия изучает свойства фигур, сохраняющихся при движениях и подобиях плоскости; аффинная геометрия изучает свойства фигур, сохраняющихся при аффинной группе преобразований; топология- при топологических преобразованиях, и т.д. То есть каждой группе преобразований соответствует своя геометрия. Этот подход впервые был предложен известным немецким математиком Феликсом Клейном.
Методическая значимость ГПП состоит в том, что они являются методом решения многих геометрических задач.
Определение 17.1: Взаимнооднозначное отображение плоскости на себя называется ГПП.
Определение 17.2: Последовательное выполнение двух или нескольких преобразований называется композицией.
![]() и
и
![]() -ГПП
-ГПП
![]()
Из определения 17.1 и 17.2 следует, что композиция двух преобразований – снова преобразование, и композиция преобразований ассоциативна, но не коммутативна.
![]() (ассоциативный
закон)
(ассоциативный
закон)
Определение 17.3: Множество геометрических преобразований плоскости G является группой, если вместе с любыми двумя преобразованиями из G в это множество включается их композиция и для любого преобразования из G в это множество включается ему обратное.
![]()
![]()
Определение 17.4: Если композиция двух преобразований есть тождественное преобразование, то каждое из них называется обратным другому.
![]()
![]() и
и
![]()
Из определений (17.1) и (17.2) следует, что множество ГПП образует группу.
Действительно,
![]() -ГПП(опр.17.1),
и
-ГПП(опр.17.1),
и
![]() -ГПП,
следовательно
-ГПП,
следовательно
![]() -группа(опр.17.3).
-группа(опр.17.3).
Групповой подход к классификации геометрии состоит в следующем: каждой группе ГПП соответствует своя геометрия, так , группа движений и подобий определяет элементарную евклидову геометрию.
§18 Движения. Их свойства. Основная теорема о движениях. Движения первого и второго рода.
Определение 18.1: ГПП, при которых сохраняется расстояние между любыми двумя точками, называется движением(D).
D(AB)=![]() AB=
AB=
Свойства движений:
1) точки, лежащие на прямой, в движении переходят в точки, лежащие на прямой и сохраняется порядок их взаимного расположения.
![]() ,
,
![]() ,
С лежит между А и В
,
С лежит между А и В
Доказать:
![]() ,
,
![]() лежит между
лежит между
![]() и
и
![]()
Доказательство:
![]()
=>
между
![]()
=> .
2) В движении прямая, луч, отрезок переходят соответственно в прямую, луч, отрезок.
Доказательство следует из определения (18.1) и свойства 1).
3) Множество движений плоскости образует группу.
3.1)![]()
3.2)
![]() т.к.
т.к.
![]()
![]()
Из 3.1 и 3.2 =>
![]() -группа.
-группа.
4) точки, не лежащие на одной прямой, в движении переходят в точки, не лежащие на одной прямой.
![]() образуют
образуют
![]()
![]()
Доказательство методом от противного:
Пусть
![]() ,
но т.к.
,
но т.к.
![]() -движение,
тогда имеем, что точки, лежащие на одной
прямой преходят в точки, не лежащие на
одной прямой, что противоречит свойству
1.
-движение,
тогда имеем, что точки, лежащие на одной
прямой преходят в точки, не лежащие на
одной прямой, что противоречит свойству
1.
5) В движении ортонормированный репер переходит в ортонормированный репер (доказательство по определению 18.1 и свойству 2)
6) (Теорема о задании движения двумя ортонормированными реперами)
Если заданы два
ортонормированных репера
![]() и
и
![]() ,
длины базовых векторов равны (
,
длины базовых векторов равны (![]() ),
то существует
),
то существует
![]()
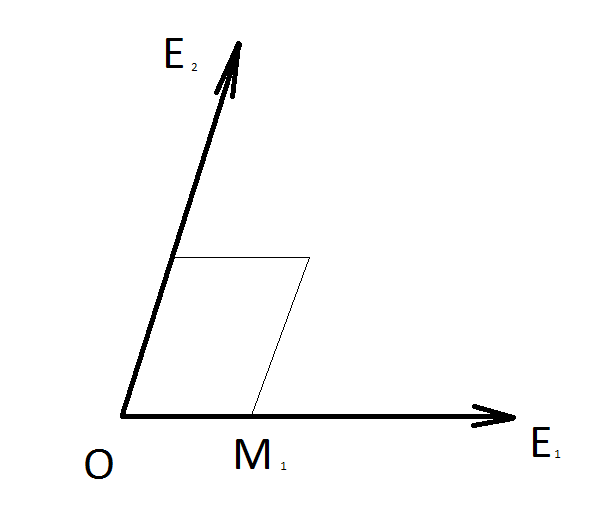

Зададим
![]() ,
где
,
где
![]()
Пусть
![]() и
и
![]() -
произвольные точки плоскости,
-
произвольные точки плоскости,
![]() ,
,
![]() в
в
![]() .
.
![]() в
в
![]() .
.
![]()
![]()
![]()
=>
![]() -
движение.
-
движение.
,
![]() ,
,
![]()
![]()
![]()
![]() .
.
7) Движение однозначно определяется двумя ортонормированными реперами, у которых длины базисных векторов равны.
8) Движение однозначно определяется двумя равными треугольниками.
9) (Координатное задание движения)
,
где
![]() ,
,
![]()
![]()
Найти формулы
движения - это все равно, что найти
зависимость между координатами
![]() и
и
![]() в
.
Но, т.к. по свойству 6)
в
.
Но, т.к. по свойству 6)
![]() ,
то нахождение искомых формул сведется
к нахождению формул перехода, а они
имеют вид:
,
то нахождение искомых формул сведется
к нахождению формул перехода, а они
имеют вид:
![]() (18.1)
(18.1)
если и одинаково ориентированны.
![]() (18.2)
(18.2)
если и противоположно ориентированны.
Где
![]() -
координаты точки в старом репере
-
координаты точки в старом репере
![]() -
координаты точки в новом репере
-
координаты точки в новом репере
Применив (18.1) и (18.2) для , получим формулы движения:
![]() (18.3)- движение
первого рода
(18.3)- движение
первого рода
или
![]() (18.4)- движение второго рода
(18.4)- движение второго рода
Определение 18.2: Движение, определенное формулой (18.3),
Называется движением первого рода, а движение, определенное формулой (18.4), называется движением второго рода.
Вывод: все движения разбиваются на два рода: