2.8Настройка параметров нейросети.

Задание функции ошибки определенного вида позволяет вычислить для каждого примера обучающей выборки оценку работы нейросети и определить направление изменения ее параметров для уменьшения значения оценки Н. Процесс итерационного изменения параметров нейросетевой функции называется обучением [40,41].

Выбор нейросетевого решателя в виде функции (4.2) позволяет применить градиентные методы оптимизации для поиска такого вектора параметров а*, который доставляет минимум выбранному функционалу ошибки, т.е. выполняется условие . Для этого вычисляются значения для каждого а_i. При использовании стандартной оценки МНК по всей выборке (4.9), имеем

	(4.13)
,	(4.14)

где S – число примеров в обучающей выборке, s – номер примера, H_s – оценка для s-го примера. Вычисление основано на формуле дифференцирования сложной функции:

.

(4.15)

В соответствии с (4.2), (4.14) для выходного (k+1-го) слоя:

,	(4.16)
	(4.17)
.	(4.18)

Мы получили формулу для вычисления производной по параметрам выходного слоя. Чтобы найти для слоя, посылающего сигналы выходному слою нейронной сети, выразим :

.

(4.19)

Тогда

,

(4.20)

где

(4.21)

– производная функции (4.3) по l – му параметру. На основе формул (4.18) – (4.21) можно рекурсивно вычислить производные по всем настраиваемым параметрам сети, что позволяет использовать тот или иной градиентный метод оптимизации, например, метод наискорейшего спуска [40], который заключается в итерационном изменении параметров в соответствие с правилом:

(4.22)

где t – номер итерации, h – шаг оптимизации. Величина шага вычисляется на каждой итерации путем одномерной оптимизации функции H(a_i,h,) при фиксированных a_i.

На практике метод (4.22) часто оказывается малоэффективным по сравнению с методами квадратичной численной оптимизации в связи со сложным рельефом функции Н. Из теории квадратичной оптимизации известно, что метод Ньютона позволяет найти минимум квадратичной формы за один шаг. Однако, поиск обратной матрицы вторых производных для всех параметров нейросети требует слишком больших вычислительных затрат, кроме этого она может не быть положительно определена, поэтому применяют методы, использующие аппроксимацию вторых производных Н по параметрам а, например BFGS-метод [41]. Известным методом этого класса является метод сопряженных градиентов [41,230]. Несмотря на то, что функция Н в общем случае не является квадратичной, метод сопряженных градиентов работает достаточно эффективно [230]. В качестве правила изменения параметров нейросети в этом случае выбирается:

(4.23)

где d_i(t) – направление оптимизации, h – шаг оптимизации.

В соответствие с [230], одной из эффективных формул, определяющих направление d_i(t), является формула Полака – Рибера (Polak – Ribiere):

,	(4.24)
где
,	(4.25)
.

На основе приведенных формул строится алгоритм градиентной оптимизации параметров нейросети:

1. Инициализация массива настраиваемых параметров а некоторыми равномерно распределенными в интервале [-0.01, 0.01] случайными величинами.

1. Вычисление F(a,x) для очередного примера задачника.

2. Вычисление Н для примера в соответствии с выбранным из (4.9)-(4.11) видом оценки.

3. Вычисление для текущего примера по формулам (4.18)-(4.21), накопление суммарного градиента.

4. Если обработаны не все примеры, перейти к п.2

5. Выбор направления оптимизации в соответствии с методом (4.22) или (4.23)-(4.25).

6. Одномерная оптимизация шага градиентного спуска h в выбранном направлении.

7. Изменение параметров а.

8. Вычисление Н.

9. Если (Н>H_min ) и (|| ||>0), то перейти к п.2, иначе - конец обучения.

При изменении параметров нейросети необходимо контролировать их значение, чтобы избежать затруднений в обучении. В случае использования функции (4.3) в качестве функции активации, диапазон наиболее эффективных значений параметров а – интервал [-1,1] [41]. Для удержания значений а в данном диапазоне применяют проективный метод контроля

(4.26)

Общей проблемой методов локальной оптимизации, к которым относятся градиентные методы, является остановка в локальных минимумах, далеких от оптимального решения. Локальный минимум характеризуется условиями: (Н>H_min ) и (|| ||0). В этом случае применяется сдвиг значений параметров нейросети в случайном направлении: а = а + , где  – равномерно распределенная на интервале [_min, _max] случайная величина. Задание значений _min, _max определяет степень изменения параметров нейросети. Интервал может постепенно увеличиваться, если изменения не приводят к выходу из локального минимума.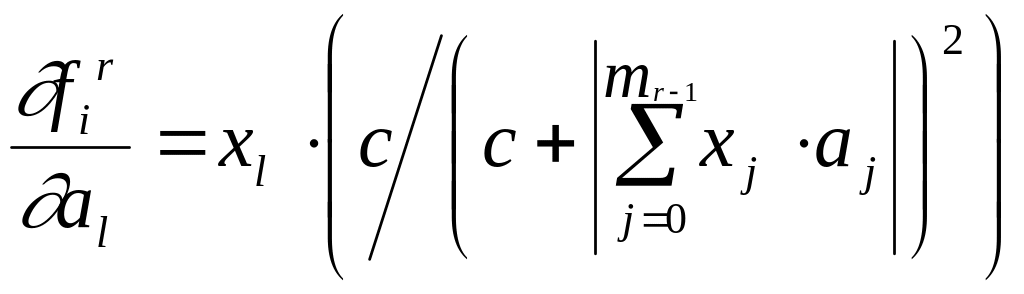