5.2.2Судно на воздушной подушке

На рис.4.4 представлено судно на воздушной подушке (СВП). Подушка создается мощным вентилятором(1), который осуществляет наддув воздуха в полость под судном, огражденную юбкой(3). Ограждение может быть резиновым, тогда судно может выходить на берег, или металлическим (чисто морской вариант). Основными движителями являются два пропеллера в насадках, тяги которых регулируются изменением шага винта . Кроме того, имеется аэродинамический руль направления .

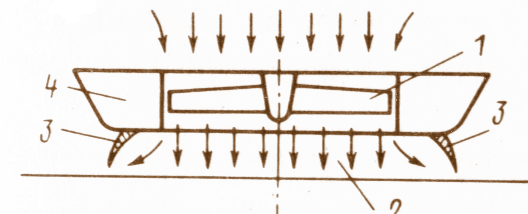
Рис.5.4

Рассматривается боковое движение судна. На движение существенно сказывается крен, поскольку при наличии крена возникают боковые силы от неравномерности струй, вытекающих из под подушки. Полагается , . Тогда рассматриваем уравнения

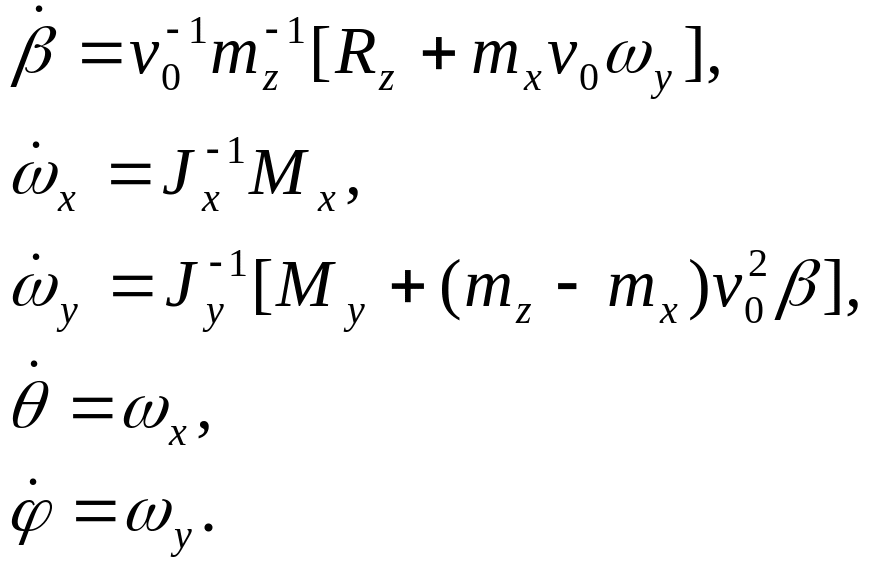(5.35)

Введем скоростной аэродинамический напор и гидродинамический напор . Обозначим -сила и моменты аэродинамического трения корпуса относительно соответствующих осей;

- сила и моменты гидродинамического трения корпуса относительно соответствующих осей;

- сила и моменты аэродинамического руля относительно соответствующих осей;

- сила и момент, создаваемые подушкой при крене;

-момент создаваемый движителями при изменении шага винта(пропеллера).

Суммарные силы и моменты

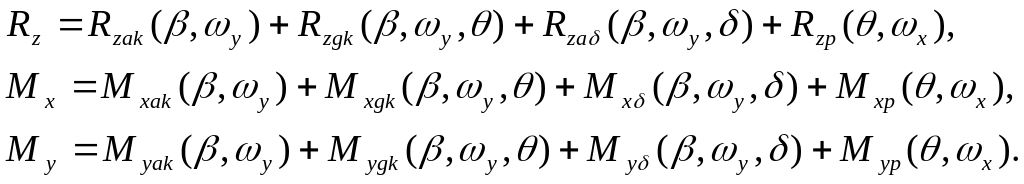
Тогда уравнения бокового движения примут вид:

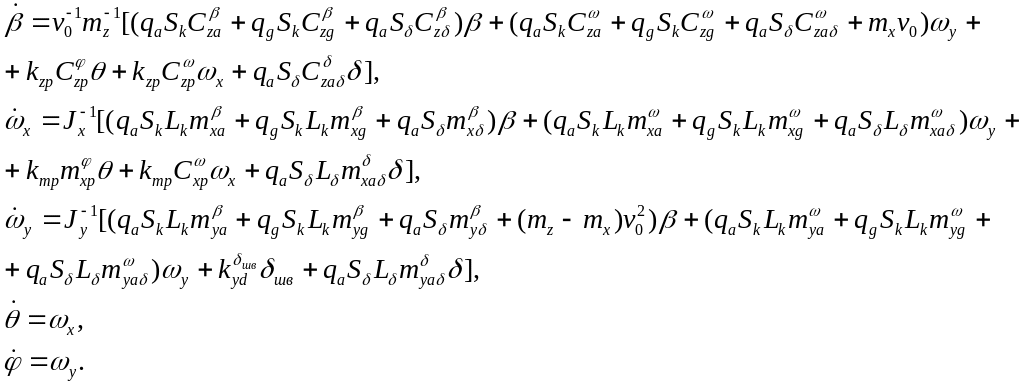(5.36)

В матричной форме эти уравнения имеют вид

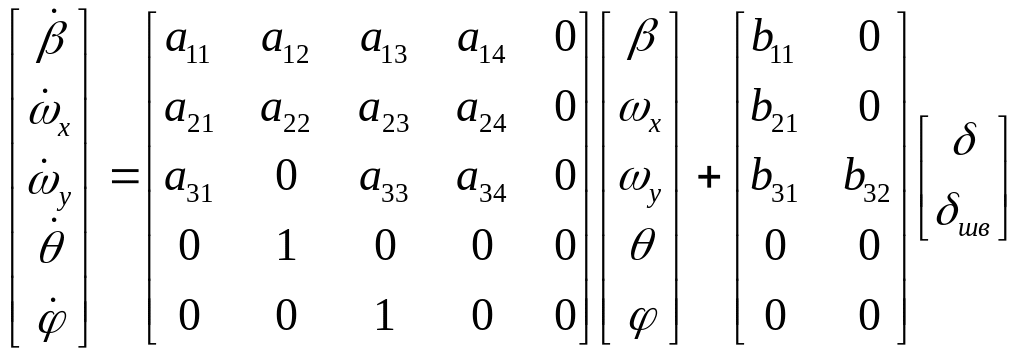. (5.37)

Система стабилизации курса СВП

Система обеспечивает стабилизацию курса ,т.е. рыскание ( .

Структура системы приведена на рис. 5.5

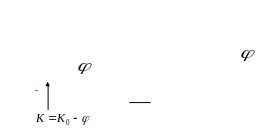
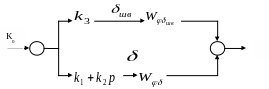
Рис.5.5

-параметры закона управления.

- передаточная функция СВП от входа к выходу ,

- передаточная функция СВП от входа к выходу .

Операторные уравнения, соответствующие системе линейных д.у. имеют вид

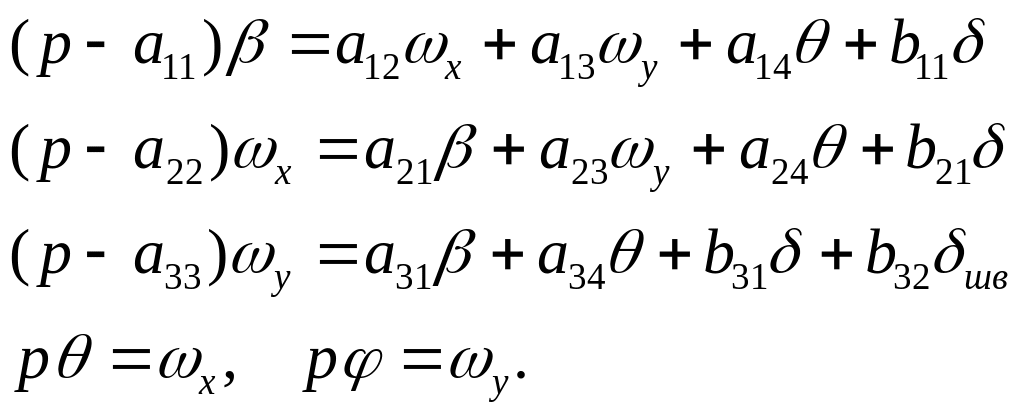
При (автоматическая стабилизация крена за счет подушки), имеем

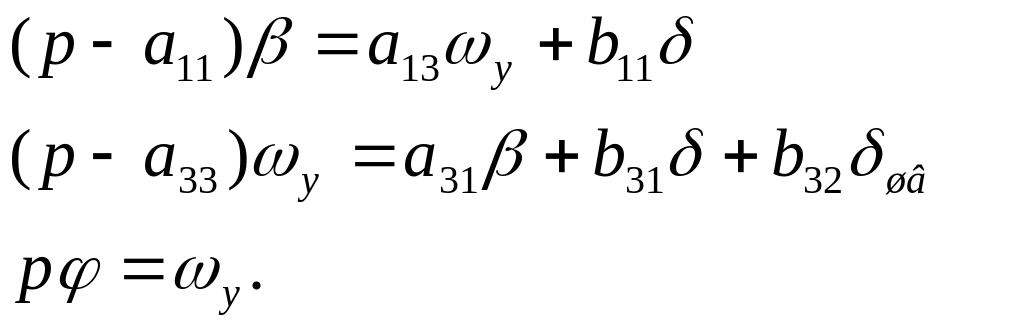
Эти уравнения аналогичны рассмотренным ранее уравнениям НК. Тогда

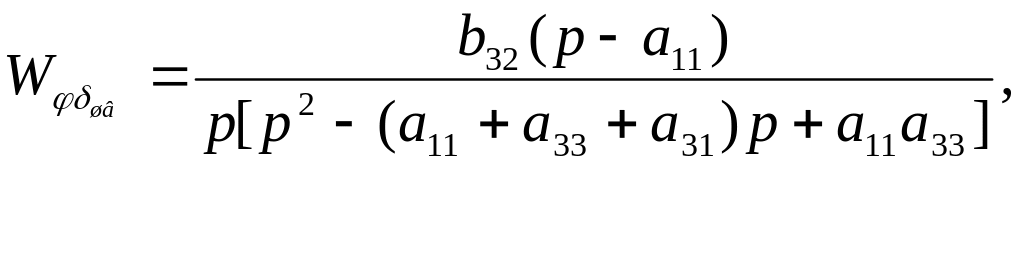
(5.38)

Передаточная функция разомкнутой системы

,

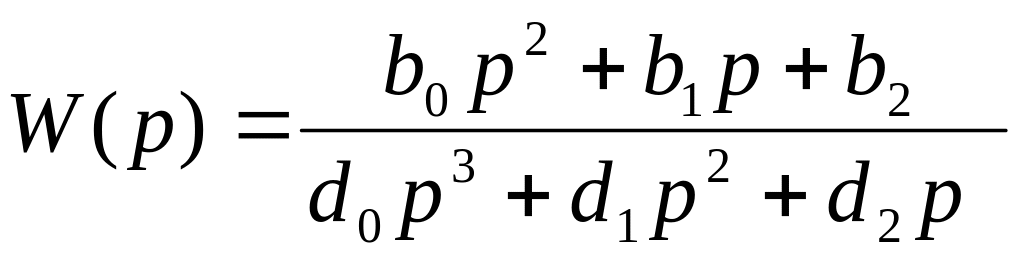где

Передаточная функция замкнутой системы

и характеристический полином можно записать

,

где .

На основании полученных коэффициентов можно провести оценку устойчивости и качества переходных процессов, как это делалось в предыдущем примере.

5.2.3Судно на подводных крыльях

Схема судна на подводных крыльях (СПК) для вертикальной плоскости представлена на рис.5.6

.

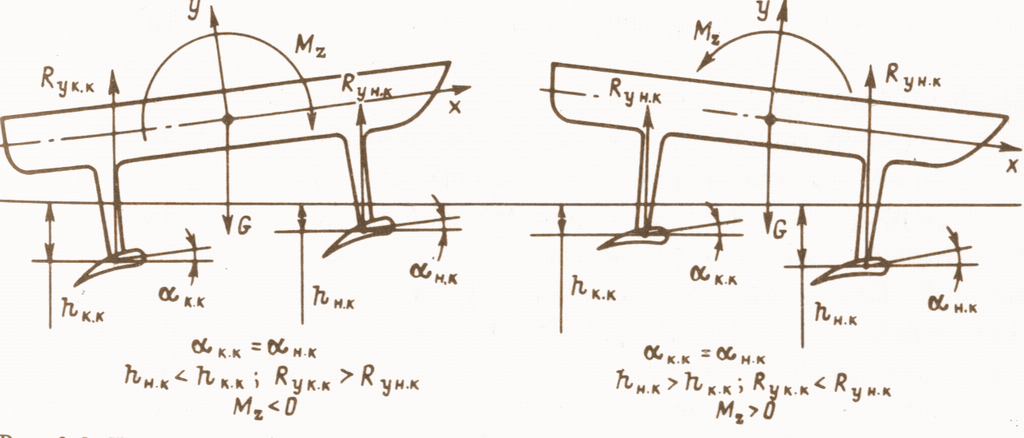
Рис.5.6

Предполагается, что скорость судна постоянна, стабилизация по дифференту и глубине погружения крыльев осуществляется за счет изменения углов атаки крыльев . Причем подъемная сила крыла увеличивается при увеличении глубины его погружения (автоматическая стабилизация дифферента). Стабилизация по крену осуществляется автоматически за счет V-образности крыльев.

Уравнения динамики СПК в вертикальной плоскости имеют вид:

(5.39)

Управляющие сила и момент имеют вид

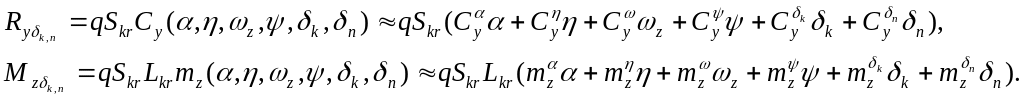
После подстановки этих силы и момента в уравнения динамики, получим

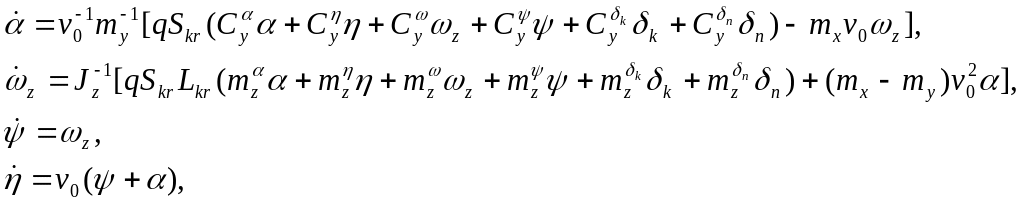(5.40)

или в векторно-матричной форме

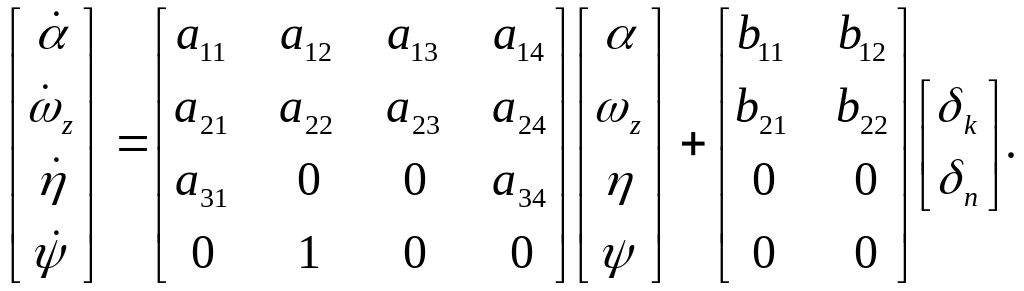
Рассмотрим систему стабилизации СПК по дифференту, рис.5.7

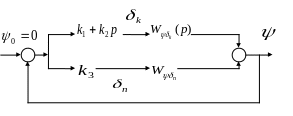
Рис.5.7

Передаточная функция разомкнутой системы имеет вид:

,

замкнутой

,

где

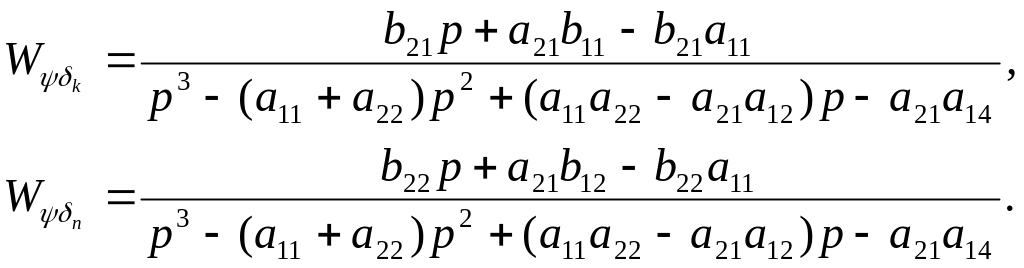(5.41)

Получив передаточную функцию замкнутой системы, ее можно исследовать на устойчивость и качество переходных процессов.