
- •Тема54.2. Примеры линеаризованных уравнений движения различных омт.-4 час. Линейные формы основных режимов движения. Построение передаточных функций для различных омт.
- •5.Балансировочные режимы
- •5.1Основные виды движения омт и упрощенные формы их представления.
- •5.2Примеры линеаризованных уравнений движения омт
- •5.2.1Надводный водоизмещающий корабль (нк)
- •5.2.2Судно на воздушной подушке
- •5.2.3Судно на подводных крыльях
- •5.2.4Автономный подводный аппарат
Тема 5.1. Линеаризация уравнений динамики и кинематики ОМТ. Основные виды движения ОМТ.-4 час. Балансировочные режимы движения. Зависимость балансировочных режимов от изменения плавучести и скорости хода ОМТ. Линеаризация нелинейных уравнения.
Тема54.2. Примеры линеаризованных уравнений движения различных омт.-4 час. Линейные формы основных режимов движения. Построение передаточных функций для различных омт.
5.Балансировочные режимы
Ранее рассматривались нелинейные уравнения динамики ОМТ вида
![]() ,
,
режимы движения, которых в большинстве
случаев предполагают установившиеся
постоянные значения параметров движения.
В этом случае
![]() ,
и установившиеся параметры движения
определяются уравнением
,
и установившиеся параметры движения
определяются уравнением
![]() =
0. (5.1)
=
0. (5.1)
Для нелинейных систем может быть
несколько решений, для линейных -
единственное
![]() .
.
Обозначим вектора значений таких
параметров как
![]() .
.
Полагая отклонения координат
![]() от
установившихся (балансировочных)
значений малыми для заданного режима
движения, можно записать их в следующем
виде
от
установившихся (балансировочных)
значений малыми для заданного режима
движения, можно записать их в следующем
виде
![]() ,
(5.2)
,
(5.2)
где
![]() -
малые отклонения. Подстановка
в
исходное нелинейное уравнение и
представление вектора
разложением
в ряд Тейлора (с учетом членов 1-го порядка
малости) позволяет представить исходное
нелинейное уравнение в виде
-
малые отклонения. Подстановка
в
исходное нелинейное уравнение и
представление вектора
разложением
в ряд Тейлора (с учетом членов 1-го порядка
малости) позволяет представить исходное
нелинейное уравнение в виде
![]() (5.3)
(5.3)
В данном уравнении
![]() ,
и уравнение можно переписать в
линеаризованном виде
,
и уравнение можно переписать в
линеаризованном виде
![]() .
(5.4)
.
(5.4)
Обычно значок
![]() опускают, частные производные вектора
по вектору представляют собой матрицы
коэффициентов и окончательно
линеаризованное уравнение имеет вид
опускают, частные производные вектора
по вектору представляют собой матрицы
коэффициентов и окончательно
линеаризованное уравнение имеет вид
![]() .
(5.5)
.
(5.5)
Линеаризация функций двух и более переменных
В уравнениях динамики весьма часто встречаются произведения двух переменных, например
![]() .
(5.6)
.
(5.6)
Или с учетом вышесказанного
![]()
![]() .
.
Кроме того полагая
![]() ,
получим
,
получим
![]() .
(5.7)
.
(5.7)
В дальнейшем рассмотрим движение ОМТ
с постоянной линейной скоростью
![]() ,
малыми углами
,
малыми углами
![]() и
нулевыми угловыми скоростями
и
нулевыми угловыми скоростями
![]() .
.
Тогда
![]() .
.
Аналогично
![]() ,
,
![]() ,
,
![]() (5.8)
(5.8)
![]() и т.д.
и т.д.
В дальнейшем будет рассматриваться линеаризация гидродинамических и управляющих сил. Обычно используется следующая форма записи суммы гидродинамических и пассивных управляющих сил и моментов
![]() ,
(5.9)
,
(5.9)
![]()
В линеаризованном виде эти уравнения имеют вид
![]() ,
(5.10)
,
(5.10)
![]()
5.1Основные виды движения омт и упрощенные формы их представления.
С учетом изложенного в разделе «Динамика»
уравнения движения ОМТ рассматриваются
в виде (принимается
![]() )
)
![]() (5.11)
(5.11)
![]()
![]()
и
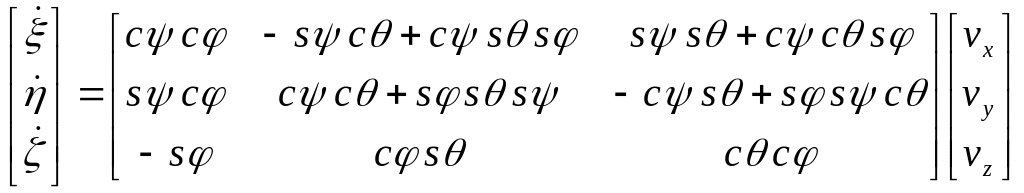 ,
(5.12)
,
(5.12)
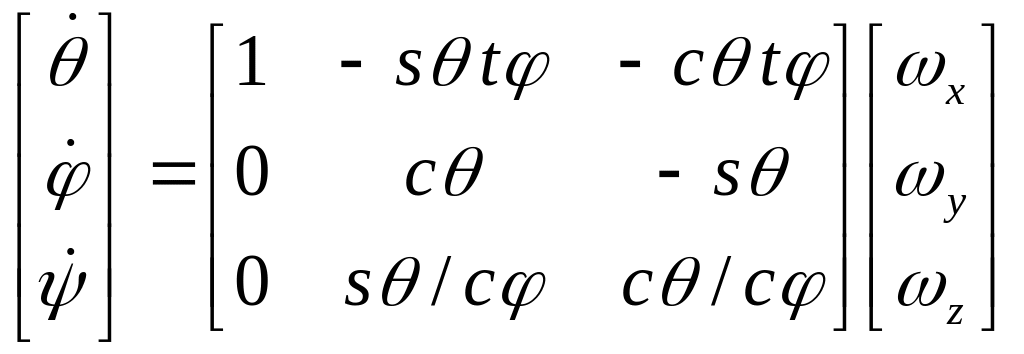 .
(5.13)
.
(5.13)
В случае малых углов Эйлера косинусы углов заменяются на единицы, а синусы или тангенсы – самими углами. Тогда рассмотренные матрицы примут вид
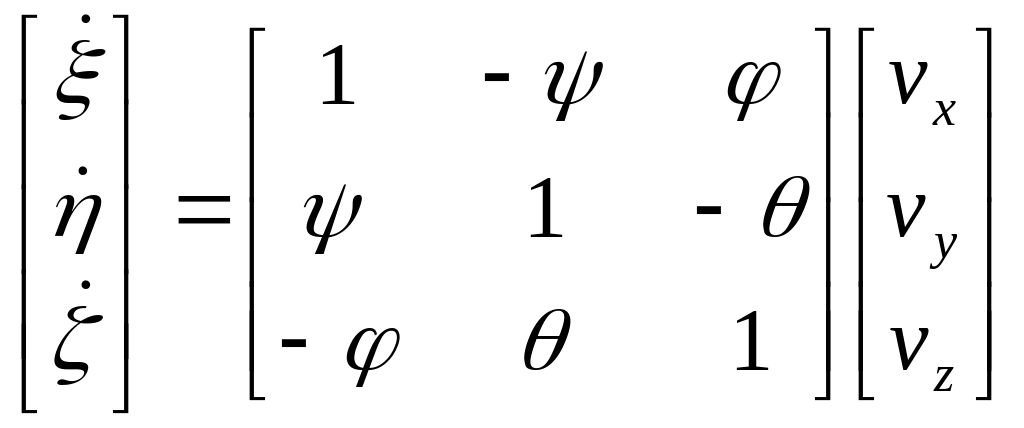 ,
,
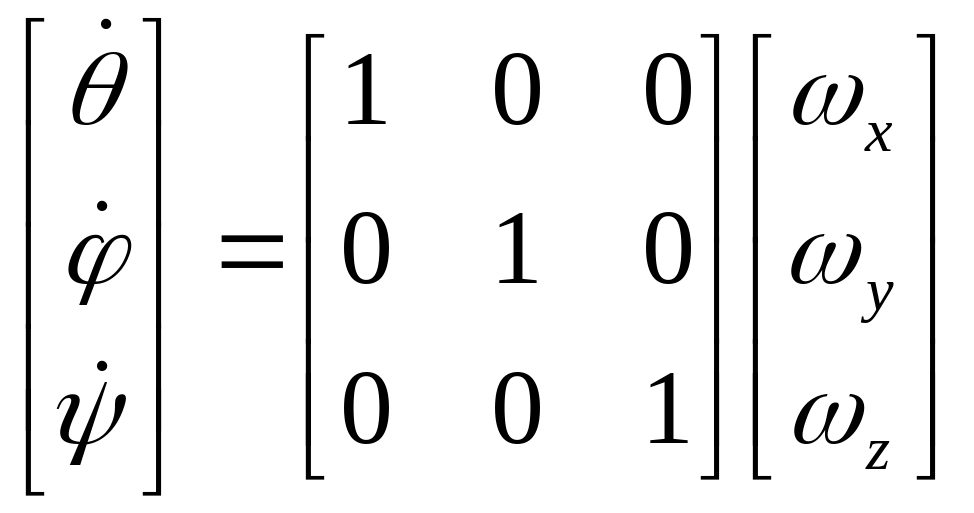 .
(5.14)
.
(5.14)
Приведенные выше уравнения динамики
могут быть разбиты на группы (для
упрощения записи внешние воздействия
![]() опущены):
опущены):
-поступательное продольное движение:
![]() (5.15)
(5.15)
- вертикальное движение:
![]() (5.16)
(5.16)
- боковое движение:
![]() (5.17)
(5.17)
- бортовая качка:
![]() (5.18)
(5.18)
-рыскание:
![]() (5.19)
(5.19)
-килевая качка:
![]() (5.20)
(5.20)
или с использованием углов атаки
![]() и дрейфа
и дрейфа
![]() и также полагая
и также полагая
![]() ,
получим
,
получим
-поступательное продольное движение:
![]() (5.21)
(5.21)
- вертикальное движение:
![]() (5.22)
(5.22)
- боковое движение:
![]() (5.23)
(5.23)
- бортовая качка:
(5.24)
-рыскание:
![]() (5.25)
(5.25)
-килевая качка:
![]() (5.26)
(5.26)
При малых углах крена![]() движения обычно разделяются по плоскостям.
движения обычно разделяются по плоскостям.
Так движение в горизонтальной плоскости описывается уравнениями
![]()
![]() (5.27)
(5.27)
Обычно гидродинамические силы на корпусе и со стороны пассивного гидродинамического руля зависят от ограниченного числа параметров движения, как то
![]() .
.
