9.4. Теория цепей.

Расчет электронных схем основан на применении уравнений теории цепей (законы Кирхгофа). Покажем, что эти законы являются следствием квазистационарного приближения для уравнений Максвелла с привлечением дополнительных сведений о цепях (сопротивление, емкость, индуктивность,…)

Задача №1. Пусть имеем систему линейных токов в замкнутых проводниках. Будем считать, что в каждом контуре протекает ток

,

где - площадь поперечного сечения проводника. Плотность тока и площадь поперечного сечения проводника зависят от координаты , отсчитываемой вдоль оси проводника. Вектор плотности тока представим в виде , где - электропроводность проводников. Циркуляция вектора по контуру представляет электродвижущую силу в виде

, (9.16)

где - сопротивление контура , - падение напряжения на сопротивлении контура, - электродвижущая сила (ЭДС) в контуре с номером . Падение напряжения зависит от величины сопротивления и не зависит от распределения плотности сопротивления по длине контура. По этой причине можно считать, что сопротивление сосредоточено в некотором произвольном месте контура. Формулу (9.16) можно записать в виде

. (9.16.А)

В электростатике первый член равен нулю. Следствием уравнения является то, что циркуляция вектора связана с изменением магнитного потока соотношением формулой

.

Здесь использовано обозначение - площадь поверхности, ограниченной замкнутым контуром .

Для замкнутого проводника соотношение (9.16.А) перепишем в виде

. (9.17)

Задача №2. В случае разомкнутого проводника, когда в месте разрыва подключена емкость (Рис. 9.1), интеграл по замкнутому контуру от можно записать в виде

.

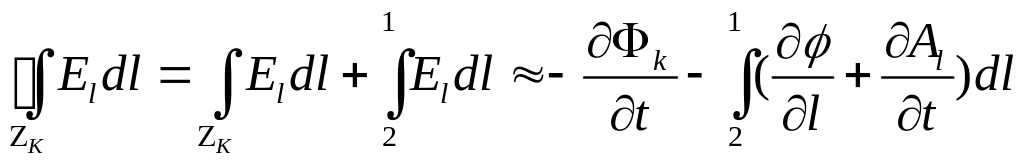В этом выражении пренебрежем слагаемым по сравнению с , поскольку электрическое поле в конденсаторе определяется в основном разностью потенциалов , а не изменением магнитного поля. Интегрирование в производится по незамкнутому контуру. Справедливо приближенное представление .

. (9.18)

Учтем представления для взаимной индуктивности и емкости:

и уравнения (9.16.А) и (9.18) объединим в виде

. (9.19)

Это второй закон Кирхгофа.

Первый закон Кирхгофа является следствием уравнения (в квазистационарном приближении при выполнении условия )

.

Имеем следствие

.

Если применить последнее равенство к узлу токов (Рис. 9.3), то придем к первому закону Кирхгофа

,

в котором, токи, вытекающие из узла считаются положительными, а втекающие - отрицательными.

Следует отметить, что законы Кирхгофа не могут быть получены на основе только уравнений Максвелла, так как для их получения необходима не содержащаяся в уравнениях Максвелла информация (сведения об объектах: сопротивлениях, емкостях и индуктивностях цепей). Уравнения Кирхгофа по этой причине качественно отличаются от уравнений Максвелла.

9.5. Скин – эффект. Выше учитывалось распределение токов вдоль проводников, но при этом не принималось во внимание распределение переменных токов по сечению проводников. На самом деле это распределение важно не только с теоретической точки зрения, но и с технической точки зрения. Ниже будет показано, что переменный ток в проводнике, в отличие от постоянного тока не распределяется равномерно по сечению проводника, а концентрируется на его поверхности. Это явление называется скин – эффект (от английского слова skin - кожа). Переменный ток как бы «выдавливает» сам себя к поверхности проводника. Это влечет за собой изменение эффективного сопротивления и самоиндукции проводника. Эти величины зависят от времени, в случае гармонических полей имеется зависимость от частоты тока. Точное решение задачи о скин – эффекте достаточно сложно – имеется зависимость не только от формы проводника, но и от способа возбуждения в нем тока.

Рассмотрим задачу о возбуждении тока гармоническим полем (рассмотрение проведем в комплексной форме, по существу можно считать, что речь идет о Фурье – образе поля) в цилиндрическом проводнике радиуса (Рис. 9.4). Проводимость проводника и его магнитную проницаемость считаем постоянными. Задачу будем решать в цилиндрической системе координат с учетом осевой симметрии . Длину проводника считаем бесконечной, свойства полей при этом не зависят от координаты . Считаем, что связь плотности тока с полем дается локальным соотношением для Фурье - образов полей

.

Как отмечалось выше, электрическое поле, в условиях квазистационарности при отсутствии стороннего тока , удовлетворяет уравнению диффузии

,

которое, благодаря условию , принимает вид

. (9.21)

Это уравнение совпадает с уравнением Бесселя для цилиндрических функций с нулевым значком ( ):

.

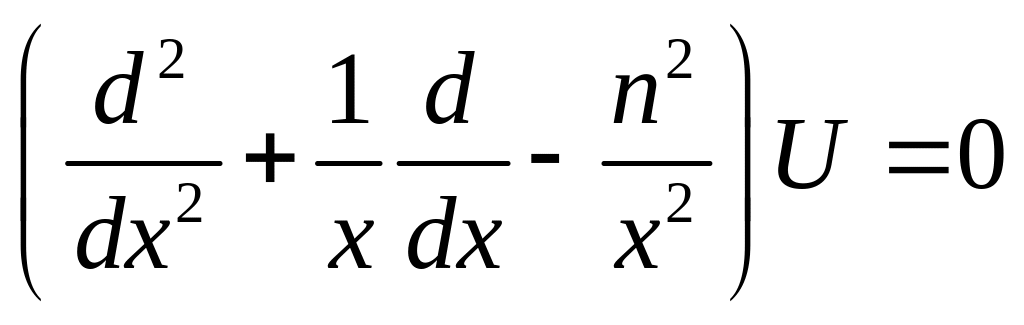Общее решение уравнения (9.21) можно взять в виде

.

Поле должно быть ограниченным внутри цилиндра и в частности при . Этому условию не удовлетворяет функция Неймана: , значит . Константа находится из граничного условия при .

В результате получаем

.

Исследуем две предельные ситуации: . Соответствующие разложения для функции Бесселя имеют вид

при

, при .

Запишем коэффициент в виде

где - глубина скин слоя. Условие соответствует требованию , т.е. радиус цилиндра должен быть много меньше глубины скин – слоя. В этом случае , это соответствует приблизительно равномерному распределению поля и плотности тока по сечению цилиндра.

Более интересен случай , - при этом должно быть: и точка наблюдения не должна приближаться к оси цилиндра. Приближенное представление поля в такой ситуации имеет вид

.

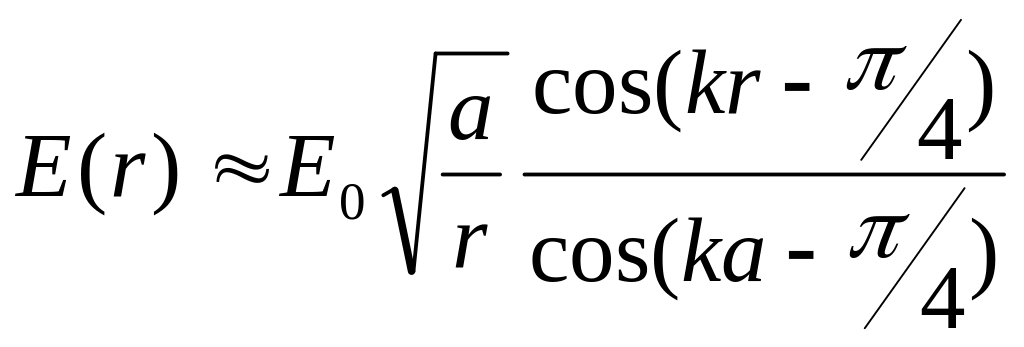Используем представление

и получим .

Таким образом, при , поле и плотность тока по абсолютной величине экспоненциально убывают при удалении точки наблюдения от поверхности цилиндра вглубь проводника. При удалении на глубину скин – слоя поле уменьшается в раз.

При расчете толщины скин – слоя предполагалось, что закон Ома имеет вид , где - электропроводность при протекании постоянного тока. Такое приближение справедливо только при условии, что поле однородно. Поле не должно изменяться существенно на расстоянии порядка длины свободного пробега электрона в металле. Это дает ограничение на глубину скин слоя . В случае поле резко неоднородно и наше рассмотрение становится неприемлемым. В этом случае реализуется аномальный скин – эффект. Выполнение условия можно добиться за счет понижения температуры (увеличивается длина свободного пробега), либо за счет увеличения частоты поля (уменьшается глубина скин - слоя).

В случае проводника с некруговым сечением точный расчет скин – эффекта представляет значительно более сложную задачу. Требуется одновременное определение поля как внутри так и снаружи проводника. Лишь в предельном случае сильного скин – эффекта задача упрощается, поскольку поле вне проводника может быть определено отдельно используя идеализацию статики и бесконечной электропроводности проводника.

9.6. Движение проводника в магнитном поле. Закон Ома для движущегося проводника. Униполярная индукция. В предыдущем рассмотрении «медленных» процессов использовался закон Ома без учета пространственной и временной дисперсий в локальной форме . Мы уже отмечали одно ограничение на использование такой формы: необходимость достаточно медленного изменения полей. Существует еще одно ограничение: неподвижность проводника относительно системы отсчета, в которой определено электромагнитное поле.

Рассмотрим ситуацию, когда проводник (или его отдельный участок) движется со скоростью относительно системы отсчета , причем , где - скорость света в вакууме. Такая ситуация называется нерелятивистской. В принципе допустима ситуация, когда и возможно рассмотрение нелинейной ситуации: . Если перейти в систему отсчета , в которой проводник покоится, то в этой системе можно использовать закон Ома . В разделе 12. «Специальная теория относительности» будет показано, что имеет место преобразование Лоренца, из которого следует

- плотность свободных зарядов.

.

Интересуясь ситуацией слабого нарушения нейтральности ( ) - подробнее об этом будет сказано в разделе 14.3 – «Обобщенный закон Ома для медленных нерелятивистских процессов»), будем иметь с точностью до членов второго порядка малости закон Ома для движущегося проводника

.

Таким образом, в движущемся проводнике сумма играет роль «эффективной» напряженности электрического поля, создающей плотность тока проводимости . Отметим, что обобщенный закон Ома представляет собой нелинейное соотношение в том случае, когда скорость зависит от электромагнитного поля.

Диссипация энергии в проводнике при протекании в нем тока не зависит от движения самого проводника. Поэтому плотность джоулева тепла, выделенная за одну секунду, дается формулой

.

СоответственноЭ.Д.С., действующая в замкнутом линейном контуре , дается интегралом

. (9.22)

Получим уравнение для описания поля в квазистационарной ситуации. Электромагнитное поле в движущихся проводниках в квазистационарном приближении описывается системой уравнений

, (9.23)

, (9.24)

.

Из закона Ома имеем . Уравнение (9.23) преобразуем

.

В однородном проводнике получается уравнение для магнитного поля

, (9.25)

где учтено , , .

Уравнение (9.25) это обобщение соответствующего уравнения квазистационарных процессов на случай движения проводника. Отметим, что такое уравнение будет присутствовать в разделе 14. «Электродинамика медленных процессов в плазме. Ионно-звуковые волны. Магнитная гидродинамика», при этом будет - скорость движения плазмы. Обсудим относительную роль конвекции (перемещение электропроводящей среды) и диффузии. Для этого сравним два члена в уравнении (9.25):

.

Это дает неравенство для ситуации преобладания конвекции над диффузией:

.

Здесь -безразмерное магнитное число Рейнольдса, - пространственный масштаб изменения полей. Если диффузия преобладает над конвекцией, то неравенство будет противоположным: . Рассмотрим эффект униполярной индукции, возникающий при вращении намагниченного проводника. Неподвижный провод присоединяется к вращающемуся магниту при помощи двух скользящих контактов А и В (Рис. 9.5). Эффект заключается в создании тока в этом проводе. Вычислим э.д.с., перейдя в систему координат, вращающуюся вместе с магнитом с угловой скоростью . В этой системе координат магнит неподвижен, а провод вращается с угловой скоростью . Согласно (9.22), с учетом , имеем э.д.с.

, где .

Эта формула и решает поставленную задачу.

9.7 . Возбуждение тока ускорением. Ускоренное движение металла эквивалентно появлению дополнительной инерционной силы (где - масса электрона, - ускорение), действующей на электроны проводимости. Сопоставим этой силе эквивалентную электрическую силу (где - заряд электрона). Должно быть . Таким образом, эффективное электрическое поле , действующее на электроны проводимости в ускоренно движущемся металле, представляет собой сумму двух полей

, (9.26)

где - электрическое поле в металле. Закон Ома принимает вид

. (9.27)

Выразим из (9.26) через и подставим в уравнение , это дает

. (9.28)

Запишем в виде суммы двух векторов

,

где - скорость поступательного движения, а - угловая скорость вращения тела. Найдем ускорение .

Рассматривается задача о движении проводника как целого (без деформаций), поэтому первые два слагаемые в правой части не зависят от координат. Третий член представляется в виде градиента . Формула (9.28) преобразуется к виду

,

где учтено соотношение .

Введем обозначение и получим уравнение

. (9.29)

Так как не зависит от координат, то уравнение можно записать в виде

. (9.30)

Уравнения (9.29) и (9.30) приводятся к уравнению для квазистационарных процессов в неподвижном проводнике

.

Вне проводника квазистационарный процесс (предполагается, что длина волны больше размеров тела) описывается уравнением . На поверхности проводника непрерывны оба вектора и . На бесконечности , .

Переменное магнитное поле индуцирует в проводнике электрический ток. В неравномерно вращающемся кольце возникает Э.Д.С. (эффект Стюарта - Толмэна).

9.8. Электромагнитные волны в линиях передачи. Телеграфные уравнения. Решение задач о распространении волн вдоль проводников связано с определенными трудностями. В электротехнике быстрых токов используется упрощенный (нестрогий) способ рассуждений, приводящий к приближенно правильным результатам. Для описания быстропеременных токов используется неприменимая для этого теория токов квазистационарных. При этом рассматривается не вся цепь в целом, а отдельные малые ее участки длины . Предполагается, что квазистационарное описание применимо к каждому такому участку.

Рассмотрим задачу о распространении волн в двухпроводной линии (система Лехера), состоящей из двух параллельных проводников (Рис. 9.6). Будем интересоваться случаем, когда длина линии и ее поперечный размер удовлетворяют условиям (здесь - длина волны). Условие квазистационарности не выполняется относительно длины линии . Не смотря на это, выделим малый участок линии длиной (Рис. 9.7) и на нем используем квазистационарное описание. Введем понятие напряжения между точками 1 и 2:

. (9.31)

В определении (9.31) интегрирование производится по - поперечной к координате. При написании (9.31) сделано пренебрежение влиянием изменения магнитного поля, использовано приближение . Это соответствует пренебрежению явлением электромагнитной индукции. Выделенный элемент системы характеризуем сопротивлением , емкостью и коэффициентом самоиндукции , где - удельные величины (на участке линии единичной длины) сопротивления, емкости и самоиндукции. При наличии утечки между проводами вводится понятие проводимости Эквивалентная схема участка линии может быть представлена в виде, изображенном на Рис. 9.8. Второй закон Кирхгофа для такой схемы дает

.

Разделив на , получим первое телеграфное уравнение

. (9.32)

Второе телеграфное уравнение напишем, применяя первый закон Киргхгофа о непрерывности тока, к точке разветвления 1 (Рис. 9.9).Здесь - втекающий в узел ток, вытекающие токи: . Первый закон Кирхгофа:

.

Разделив на , получим второе телеграфное уравнение

. (9.33)

Система телеграфных уравнений (9.32) и (9.33) описывает эволюцию и в длинной линии при заданных значениях параметров . Следует отметить, что телеграфные уравнения не могут быть получены на основе только уравнений Максвелла, так как для их получения необходима не содержащаяся в уравнениях Максвелла информация (сопротивления, емкости и индуктивности длинных линий). Телеграфные уравнения так же как уравнения Кирхгофа по этой причине качественно отличаются от уравнений Максвелла.

В частности, в линии без потерь ( ) система (9.32) и (9.33) приводится дифференциальному уравнению второго порядка для и для :

, , .

Здесь - скорость распространения волны напряжения и волны тока. Общее решение этих уравнений имеет вид

, ,

где - произвольные функции. Функции описывают волны, распространяющиеся в направлении , а функции описывают волны, распространяющиеся в сторону .

Получим связь между волнами, распространяющимися в одну сторону, например . Из второго телеграфного уравнения (9.33) имеем

.

Переходя к переменной , получим обыкновенное дифференциальное уравнение

.

Интегрируя это уравнение и полагая равной нулю константу интегрирования, получаем связь волны напряжения с волной тока

.

Параметр имеет размерность сопротивления и называется волновым сопротивлением линии передачи. Для волн, перемещающихся в обратном направлении, имеет место связь

.

Большое применение имеет двухпроводная линия в виде коаксиального кабеля. Для него были получены формулы для емкости и индуктивности элемента длины и для единицы длины кабеля

,

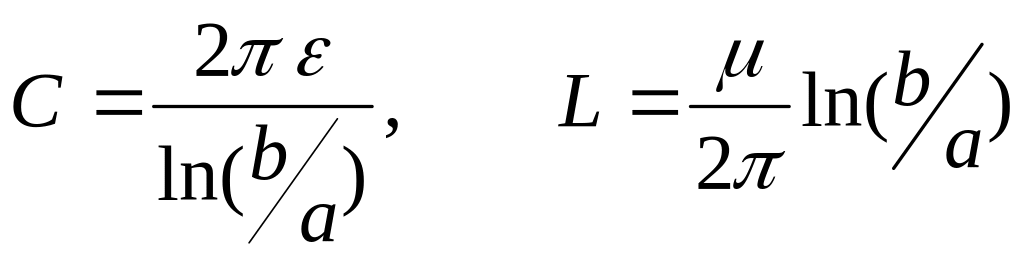где - диэлектрическая и магнитная проницаемости среды между внутренним и внешним проводниками ( - их диаметры). Скорость распространения волн в кабеле представляется в виде , - скорость света в вакууме. Таким образом, за счет выбора среды заполнения можно замедлять скорость распространения волн в кабеле. Волновое сопротивление кабеля представляется в виде

9.9. Гармонический процесс в длинной линии. Общее решение уравнения для напряжения в длинной линии без потерь представляется суммой двух волн, распространяющихся в противоположных направлениях

.

Частным случаем таких волн являются гармонические волны

где - произвольные постоянные, ниже возьмем . Учитывая связь волн тока с волнами напряжения, имеем

Таким образом, общее решение телеграфных уравнений в данной задаче имеет вид

где - две произвольные константы.

Рассмотрим конкретную ситуацию: процесс в полу бесконечной линии с сопротивлением нагрузки при (Рис. 9.9). В этой точке должно выполняться условие , которое дает . Параметр имеет смысл коэффициента отражения волны напряжения. Рассмотрим предельные случаи:

1). .

2). .

3). .

Рассмотрим теперь процесс в линии конечной длины. На концах линии задаем условия

.

Получаем ,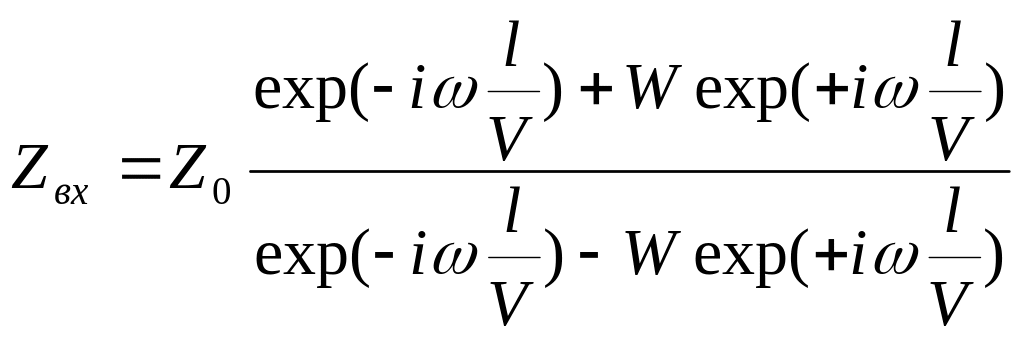

.

Рассмотрим предельные случаи:

1).

2).

3).

При и входное сопротивление длинной линии чисто мнимое и изменяется периодически при изменении длины линии (период находится из условия ). Область соответствует емкостному сопротивлению, а область соответствует индуктивному сопротивлению.

В заключение изобразим эпюры напряжений в разомкнутой линии в разные моменты времени после подключения источника напряжения. Эта ситуация выходит за рамки рассмотрения гармонических процессов. Коэффициент отражения для напряжения от разомкнутого конца линии . Считается, что источник не имеет внутреннего сопротивления. Коэффициент отражения волны напряжения от источника (от короткого замыкания) . (Рис.9.10). Имеет место периодический процесс.