
- •3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •4. Знакочередующиеся ряды. Признак Лейбница.
- •5. Знакопеременные ряды. Теорема о сходимости знакопеременного ряда.Абсолютная и условная сходимость знакопеременных рядов. Свойства абсолютно сходящихся рядов.
- •6. Функциональные ряды. Сходимость и сумма ряда. Область сходимости.
- •7. Равномерная сходимость функциональных рядов. Признак Вейерштрасса.
- •Признак равномерной сходимости.
- •1) Признак Вейерштрасса (мажорантный признак)
- •8. Интегрирование и дифференцирование функциональных рядов.
- •9. Степенные ряды. Теорема Абеля. Радиус сходимости. Вычисление радиуса
- •10.Ряды Тейлора и Маклорена.
- •11.Достаточные условия разложения функции в ряд Тейлора.
- •13.Применение степенных рядов к вычислению интегралов, значений функций, решению ду.
- •Приближенное решение ду с помощью степенных рядов
- •1.Способ последовательного дифференцирования
- •2.Способ неопределенных коэфф.
- •14. Тригонометрическая система функций и ее свойства.
- •15. Тригонометрический ряд. Сходимость. Ряд Фурье. Коэффициенты Фурье.
- •20.Приближение в среднем функции тригонометрическими полиномами.
- •21.Неравенство Бесселя.
- •22.Интеграл Фурье. Синус и косинус преобразование Фурье.
- •23.Ряд Фурье в комплексной форме.
- •24.Интеграл Фурье в комплексной форме.
- •25.0Пределение и область существования функции комплексной переменной (фкп).
- •26.Предел и непрерывность фкп.
- •27.Дифференцирование фкп.
- •27.Дифференцирование фкп
- •28.Геометрический смысл модуля и аргумента производной фкп.
- •29.Аналитичность фкп. Условия Коши-Римана.
- •30.Интегрирование фкп.
- •3L.Интегральная формула Коши.
- •32.Степенные ряды фкп. Радиус и круг сходимости.
- •34.Ряд Лорана и область его сходимости.
- •35.0Собые точки и их классификация.
- •36.Вычеты фкп.
- •37.Применение вычетов к вычислению интегралов.
- •3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).
20.Приближение в среднем функции тригонометрическими полиномами.
Представление ф-ции бесконечным рядом имеет на практике тот смысл, что конечная сумма, получающаяся при обрывании ряда на n-м члене, является приближенным выражением.
Приближенное
представление периодической функции
f(x)
тригонометрическим многочленом вида:
![]()
Рассмотрим
функцию y=f(x)
на [a, b].
Оценим погрешность при замене этой
ф-ции ф-цией
![]() .
За меру погрешности можно взять
.
За меру погрешности можно взять
![]() на
[a, b] –
наибольшее уклонение. Но берут среднее
квадратичное уклонение
на
[a, b] –
наибольшее уклонение. Но берут среднее
квадратичное уклонение
![]() :
:
![]() .
.
Среди всех тригонометрических многочленов порядка n наименьшее среднее квадратичное уклонение от ф-ции f(x) имеет тот многочлен, коэф. которого – коэф. Фурье функции f(x).
Величина
наименьшего квадратичного уклонения:
![]()
Т.
к.
![]() ,
то при любом n:
,
то при любом n:
![]() - неравенство Бесселя.
- неравенство Бесселя.
Можно
показать, что если ф-ция f(x)
явл. кусочно-монотонной, то при
![]() это неравенство превращается в равенство
Парсеваля-Ляпунова.
это неравенство превращается в равенство
Парсеваля-Ляпунова.
21.Неравенство Бесселя.
Среди всех тригонометрических многочленов порядка n наименьшее среднее квадратичное уклонение от ф-ции f(x) имеет тот многочлен, коэф. которого – коэф. Фурье функции f(x).
Величина наименьшего квадратичного уклонения:
Т. к. , то при любом n: - неравенство Бесселя.
Можно показать, что если ф-ция f(x) явл. кусочно-монотонной, то при это неравенство превращается в равенство Парсеваля-Ляпунова.
22.Интеграл Фурье. Синус и косинус преобразование Фурье.
Пусть
имеем f(x),
определенную на (![]() )
и абсолютно интегрируемую на этом
интервале,т.е.
)
и абсолютно интегрируемую на этом
интервале,т.е.
![]() (конечное
число),фун-ция разлагается в ряд на
(-l,l).
(конечное
число),фун-ция разлагается в ряд на
(-l,l).
![]() ;
;![]() ;
;
![]() ;
;![]()
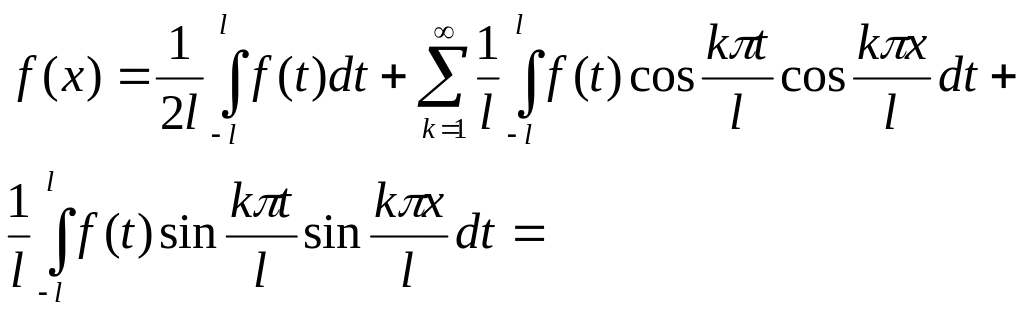
![]() |
|![]() |=
|=
(Умножим
и поделим на
![]() )=
)=![]()
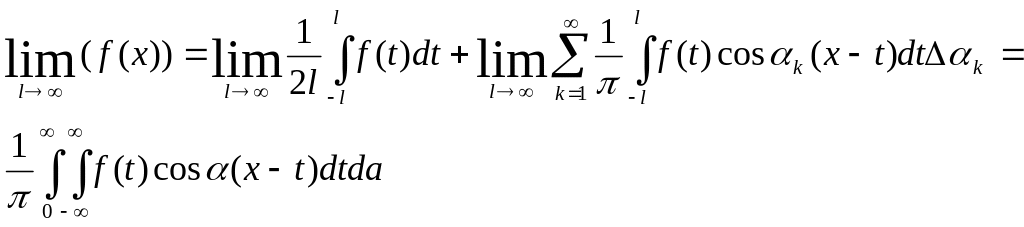 (1)
(1)
(1)- Интеграл Фурье
Если ф-ция четная или нечетная, то частные случаи:
Распишем
интеграл:![]()
1)f(x)-четная
![]()
![]() -
cos преобразование Фурье
-
cos преобразование Фурье
2)f(x)-нечетная
![]()
![]() -
обратное преобразование от cos
преобразования
-
обратное преобразование от cos
преобразования
![]() -
sin преобразование Фурье
-
sin преобразование Фурье
![]() -
обратное преобразование sin
преобразование Фурье
-
обратное преобразование sin
преобразование Фурье
23.Ряд Фурье в комплексной форме.
![]() ;
;![]() ;
;![]() ;
;![]()
![]()
![]()
![]()
![]() интеграл
Ф. В комплексной формуле при (
интеграл
Ф. В комплексной формуле при (![]() ):
):![]()
24.Интеграл Фурье в комплексной форме.
В
действ. форме:
![]()
Возьмем:
![]()
При
l =![]() :
:
![]()
![]() +
+
![]() =
=
![]() = | По формулам Эйлера => | =
= | По формулам Эйлера => | =
![]() =
=
![]() — Интеграл Фурье в комплексной форме;
или:
— Интеграл Фурье в комплексной форме;
или:
=
![]() = | введем новую переменную: с(α)
=
= | введем новую переменную: с(α)
=
![]() | = =
| = =![]() — также интеграл Фурье в комплексной
форме
— также интеграл Фурье в комплексной
форме
25.0Пределение и область существования функции комплексной переменной (фкп).
E, k — множества значений w = f(z)
z, w — их переменные
Если переменной z из множества E становится в соответствие значение w из множества k (одно или несколько), то w называется функцией от z.
Если одному значению z становится в соответствие одно значение w — функция однозначна, если несколько — многозначна.
Если переменная z задается в обл. D, а w в области g, то D — область определения, а g — область значений функции w.
26.Предел и непрерывность фкп.
Предел ФКП.
W=f(z) – однозначна и определена во всех точках (за исключением z=zo).
Предел функции W в точке zo – такое число А, что, задав любое ε>0, можно указать такое δ>0, для всех значений z, | z-zo | < δ, выполняется неравенство | f(z)-A | < ε
lim W= lim f(z)=A, где А=В+iС.
z→zo z→zo
Теорема. Если существует limf(z), и он равен А, где А=В+iС, то существует
z→zo
limU(x,y), и он равен В, и существует limυ(x,y)=С.
x→xo x→xo
y→yo y→yo
Доказательство: по определению предела
| f(z)-A | < ε
т.к. zo=xo+iyo,
f(z)= U(x,y)+iυ(x,y)
| U(x,y)+iυ(x,y)-(B+iC) | < ε
| U-B-i(υ-C) | < ε и | x+iy-(xo+iyo) | < ε (по определению)
| (U-B)+i(υ-C) |=sqrt((U-B)2+( υ-C)2) < ε и | (x-xo)+i(y-yo) |=sqrt((x-xo)2+( y-yo)2) < ε
| U-B | < ε и | υ-C | < ε, при | x-xo | < δ и | y-yo | < δ,
т.е. limU(x,y), и он равен В, и существует limυ(x,y)=С.
x→xo x→xo
y→yo y→yo
Согласно данной теореме, свойства пределов справедливы для ФКП.
Определение. Предел функции W=f(z) при z→∞, называется число А, что, задав любое >0, можно указать такое N>0, что для всех | z | > N выполняется неравенство | f(z)-A | < ε
lim f(z)=A (предел бесконечной точки).
z→∞
Непрерывность ФКП.
Функция W=f(z) определена в некоторой замкнутой области Д и zоєД.
Определение. Функция W=f(z) называется непрерывной в точке zо, если предел
lim f(z)= f(zо)≠0.
z→zo
Функция называется непрерывной в области Д, если она непрерывна в любой точке этой области.
limU(x,y)= U(xо,yо) и limυ(x,y)= υ(xо,yо)
x→xo x→xo
y→yo y→yo
Если f(z) непрерывна в точке zo, то и функция U(x,y) и υ(x,y) непрерывны в точке (xо,yо).
Теорема о непрерывности действительной функции подходит для ФКП, за исключением неравенств.
Определение. Функция f(z) называется непрерывной в бесконечно удалённой точке z=∞, если предел f(z) при z→∞ равен Wo (конечному числу) и это число может выходить за область значений функции.
