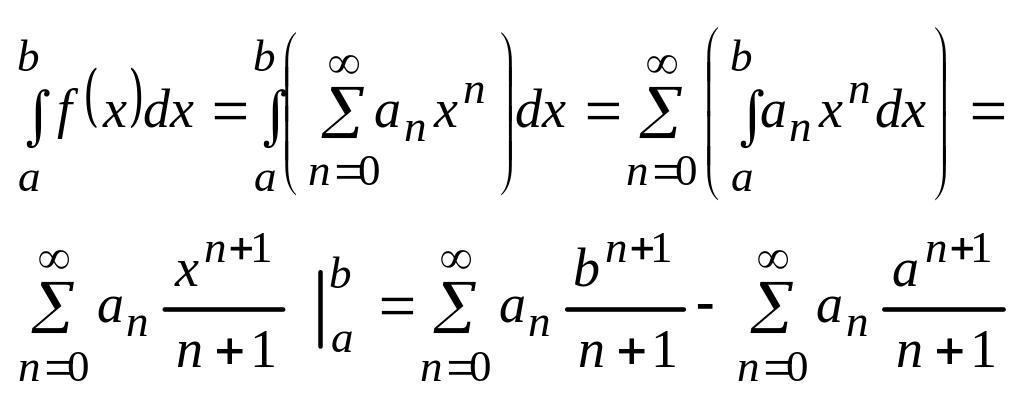- •3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •4. Знакочередующиеся ряды. Признак Лейбница.
- •5. Знакопеременные ряды. Теорема о сходимости знакопеременного ряда.Абсолютная и условная сходимость знакопеременных рядов. Свойства абсолютно сходящихся рядов.
- •6. Функциональные ряды. Сходимость и сумма ряда. Область сходимости.
- •7. Равномерная сходимость функциональных рядов. Признак Вейерштрасса.
- •Признак равномерной сходимости.
- •1) Признак Вейерштрасса (мажорантный признак)
- •8. Интегрирование и дифференцирование функциональных рядов.
- •9. Степенные ряды. Теорема Абеля. Радиус сходимости. Вычисление радиуса
- •10.Ряды Тейлора и Маклорена.
- •11.Достаточные условия разложения функции в ряд Тейлора.
- •13.Применение степенных рядов к вычислению интегралов, значений функций, решению ду.
- •Приближенное решение ду с помощью степенных рядов
- •1.Способ последовательного дифференцирования
- •2.Способ неопределенных коэфф.
- •14. Тригонометрическая система функций и ее свойства.
- •15. Тригонометрический ряд. Сходимость. Ряд Фурье. Коэффициенты Фурье.
- •20.Приближение в среднем функции тригонометрическими полиномами.
- •21.Неравенство Бесселя.
- •22.Интеграл Фурье. Синус и косинус преобразование Фурье.
- •23.Ряд Фурье в комплексной форме.
- •24.Интеграл Фурье в комплексной форме.
- •25.0Пределение и область существования функции комплексной переменной (фкп).
- •26.Предел и непрерывность фкп.
- •27.Дифференцирование фкп.
- •27.Дифференцирование фкп
- •28.Геометрический смысл модуля и аргумента производной фкп.
- •29.Аналитичность фкп. Условия Коши-Римана.
- •30.Интегрирование фкп.
- •3L.Интегральная формула Коши.
- •32.Степенные ряды фкп. Радиус и круг сходимости.
- •34.Ряд Лорана и область его сходимости.
- •35.0Собые точки и их классификация.
- •36.Вычеты фкп.
- •37.Применение вычетов к вычислению интегралов.
- •3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).
9. Степенные ряды. Теорема Абеля. Радиус сходимости. Вычисление радиуса
сходимости.
Степенным
рядом называется функциональный ряд
вида
![]() ,
где
,
где
![]() - постоянные числа, называемые
коэффициентами ряда.
- постоянные числа, называемые
коэффициентами ряда.
Теорема Абеля.
Если
степенной ряд сходится при некотором
значении
![]() ,
не равном нулю, то он абсолютно сходится
при всяком х, для которого
,
не равном нулю, то он абсолютно сходится
при всяком х, для которого
![]() .
.
Если
ряд расходится при некотором значении
,
то он расходится при всяком х, для
которого
![]() .
.
Доказательство:
Так как по предположению числовой ряд
![]() сходится, то его общий член
сходится, то его общий член
![]() при
,
а это значит, что существует такое
положительное число М, что все члены
ряда по абсолютной величине меньше М.
Перепишем ряд в виде
при
,
а это значит, что существует такое
положительное число М, что все члены
ряда по абсолютной величине меньше М.
Перепишем ряд в виде
![]() и
рассмотрим ряд из абсолютных величин
его членов:
и
рассмотрим ряд из абсолютных величин
его членов:
![]() Члены
этого ряда меньше соответствующих
членов ряда
Члены
этого ряда меньше соответствующих
членов ряда
![]()
При
последний ряд представляет собой
геометрическую прогрессию со знаменателем
![]() и, следовательно, сходится.
и, следовательно, сходится.
Теперь
нетрудно доказать и вторую часть теоремы:
пусть в некоторой точке
ряд
расходится. Тогда он будет расходиться
в любой точке х, удовлетворяющей условию
.
Действительно, если бы в какой-либо
точке х-, удовлетворяющей этому условию,
ряд сходился, то в силу только что
доказанной первой части теоремы он
должен был бы сходиться и в точке
,
так как
![]() .
Но это противоречит условию, что в точке
ряд расходится. Следовательно, ряд
расходится и в точке х. Теорема полностью
доказана.
.
Но это противоречит условию, что в точке
ряд расходится. Следовательно, ряд
расходится и в точке х. Теорема полностью
доказана.
Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.
10.Ряды Тейлора и Маклорена.
Пусть ф-я f(x) является бесконечно диффериенцируемой, тогда этой ф-и можно поставить в соответствие ряд
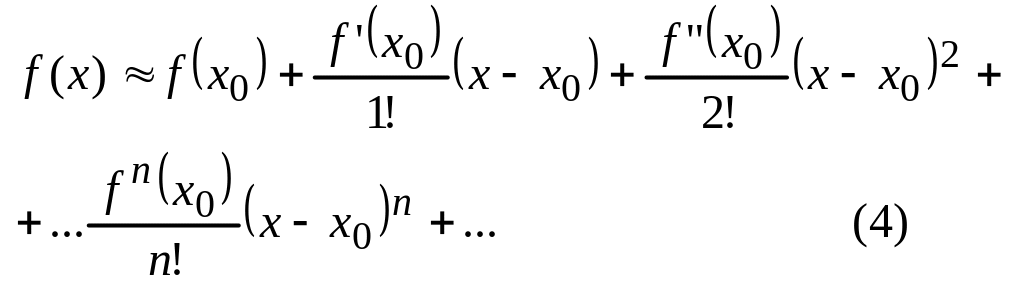
Когда
x00,
то
![]()
В интервале сходимости (-R;R) сумма этого ряда S(x), но не всегда f(x)=S(x).
Если ряд сходится, то его можно представить в виде Sn(x)+rn(x) Pn(x)+Rn(x) и Sn(x)=Pn(x), значит rn(x)=Rn(x) иначе не равны.
11.Достаточные условия разложения функции в ряд Тейлора.
Если все производные ограничены одной и той же константой, то ряд Тейлора сходится к ф – и по x.
![]()
![]()
![]() - сходится по
признаку Даламбера.
- сходится по
признаку Даламбера.
У
сходящегося общий член ряда
![]()
![]() ,
отсюда следует, что
,
отсюда следует, что
![]()
Пусть f(x) бесконечно дифференцируема и
![]() Является
ли этот ряд рядом Тейлора?
Является
ли этот ряд рядом Тейлора?
![]()
![]() ………………………………………………………….
………………………………………………………….
![]() .
.
Пусть
x=x0,
тогда
![]() ,
,
![]() или
или
![]()
f(x) – ряд Тейлора.
12.Разложение в ряд Тейлора элементарных функций (sin х, cos х, е в степени X , 1n(l +х), (1 +х) в степени Alfa).
1.
![]()
![]()
2.
![]()
f(0)=0
![]()
![]()
![]()
![]()
![]()
![]()
3.
![]()
![]()
![]() .
.
4)![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
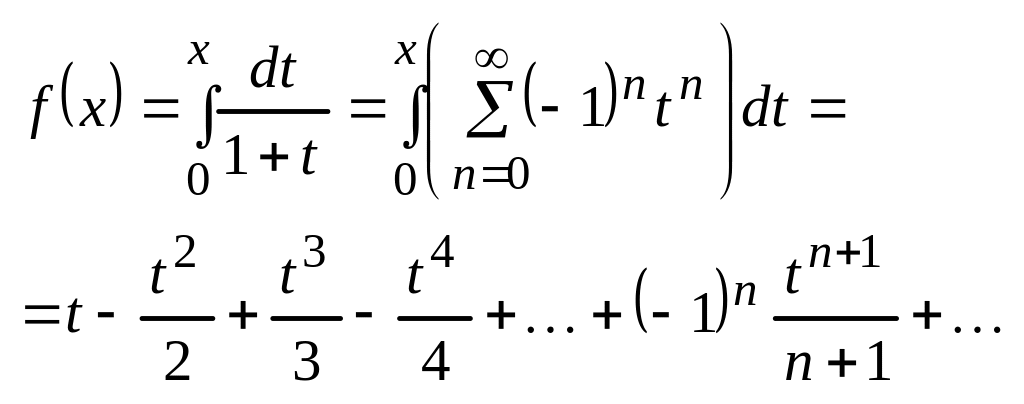
![]()
при
X=1 ряд тоже сходится
![]()
![]()
5)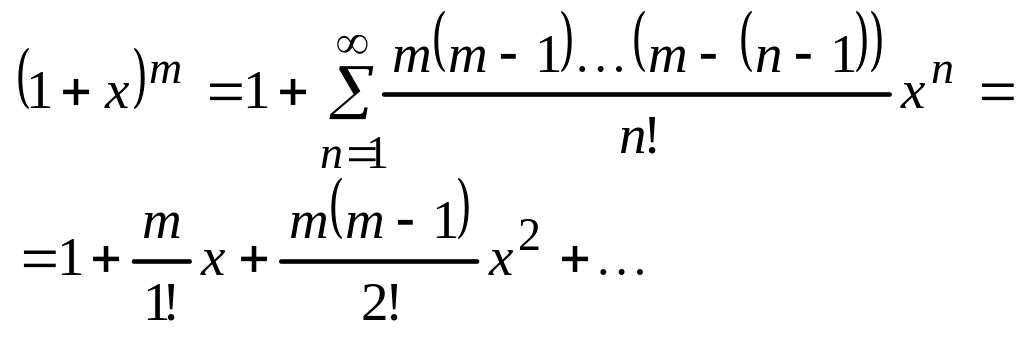 ;
;
![]() .
.
13.Применение степенных рядов к вычислению интегралов, значений функций, решению ду.
Приближенное вычисление значений ф-ций.
![]() -
входит в обл. сходимости.
-
входит в обл. сходимости.
Подставляют
![]()
![]()
В
зависимости от того, с какой точностью
требуется вычислить
![]() оставляют достаточное число членов
этого числового ряда. Достаточное число
слагаемых берут из оценки достаточного
члена ф-лы Тейлора или ост члена ряда
Тейлора. Либо для знакочередуюшегося
ряда, используя следствие из признака
Лейбница.
оставляют достаточное число членов
этого числового ряда. Достаточное число
слагаемых берут из оценки достаточного
члена ф-лы Тейлора или ост члена ряда
Тейлора. Либо для знакочередуюшегося
ряда, используя следствие из признака
Лейбница.
Для
вычисления определенных интегралов
![]()
Подинтегральную ф-цию разлагают в ряд Маклорена и в области равномерной сходимости возможно почленное интегрирование