15. Этапы построения математической модели
1)анализ изучаемой проблемы, ситуации, которую мы хотим смоделировать
2)структурирование проблемы (т.е., цель, управляемые и неуправляемые факторы, множество возможных решений, ограничения, критерии, лпр)
3) выделение наиболее существенных управл. и неуправл. факторов
4)обратиться к библиотеке существующих мат. моделей. Далее:
a. если такая модель существует, то переходим к этапу «модель построена»
б. если такой модели не существует, то переходим к следующему этапу
5) связать между собой упр. и неупр. факторы в математические конструкции, которые бы отражали причинно-следственные связи между ними
6) окончательно сформулировать мат. модель
7) модель построена
16. Этапы моделирования
1) построение математической модели
2) решение мат. модели
3)проверка адекватности мат. модели ( должна быть непротиворечива, может быть проверена на операциях, проводимых ранее; использование имеющихся данных):
а. если модель адекватна, то можно проводить моделирование (этап 4)
б. если неадекватна, то необходимо вернуться в начало и пересмотреть модель
4) проведение математического моделирования
5) принятие решения лпр
17. Виды математических моделей. Примеры
1)линейные: содержат только линейные функции переменных (например, f(х)=a*x)
2) нелинейные: содержат любые функции, отличные от линейных (например, f(x)=a*x+b*(x^2))
3)статические: изменение параметров и переменных во времени не рассматривается
4) динамические: описывают изменение параметров во времени
При этом, {скорость изменения моделируемой величины во времени}={сумма изменений во времени всех причин, вызывающих изменение моделируемой величины} – уравнение баланса моделируемой величины
Пример: модель Мальтуса (получение динамики изменения народонаселения во времени)
5) детерминированные: модели, в которых абсолютно все известно
6) стохастические и в условиях полной неопределенности: неопределенность может рассматриваться как случайная величина и, напротив, величиной, к которой применение методов теории вероятности и мат статистики в принципе невозможно
7) оптимизационные: описывают операции, в которых необходимо найти оптимальное и наилучшее решение
18. Линейные мат. модели. Примеры
Содержат только линейные функции переменных (например, f(х)=a*x)
19. Нелинейные мат. Модели. Примеры
содержат любые функции, отличные от линейных (например, f(x)=a*x+b*(x^2))
20. Стационарные математические модели. Примеры
?????????????????????????????????????????????????????????????????????????????????
21. Динамические мат. модели. Примеры. Модель Мальтуса и Ферхюльста – мат.модели и их графическая интерпретация. Мат. модель рекламной компании
описывают изменение параметров во времени
При этом, {скорость изменения моделируемой величины во времени}={сумма изменений во времени всех причин, вызывающих изменение моделируемой величины} – уравнение баланса моделируемой величины
Соответственно, если фактор вызывает возрастание моделируемой величины, то он входит в правую часть со знаком +, а если приводит к убыванию – со знаком -. Скорость же измеряется ее первой производной по времени.
Модель Мальтуса (получение динамики изменения народонаселения во времени). Согласно ей, скорость изменения численности населения определяется двумя факторами – рождаемостью и смертностью.
dN(t)/dt={рождаемость}-{смертность}
{рождаемость}=λ*N(t); {смертность}= β*N(t), где - коэф. Рождаемости (=кол-во рождений/100 000 чел./день), а - коэф. Смертности ( = кол-во смертей/100 000 чел./день)
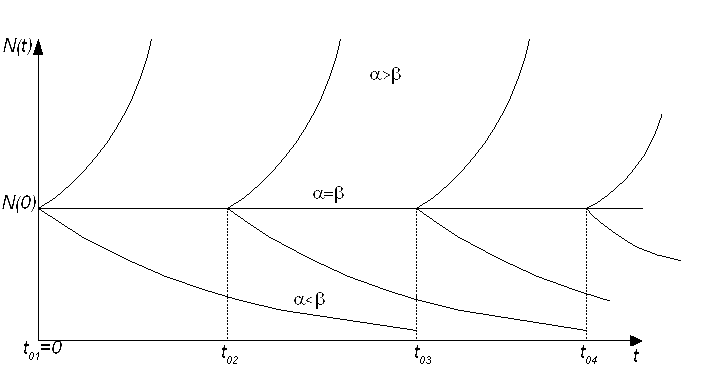
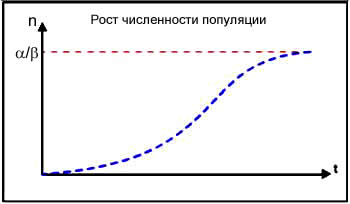
Модель Ферхюльста(в отличие от модели Мальтуса) учитывает ограниченность и таких факторов, как жизненное пространство и необходимые ресурсы. Таким образом, в данной модели смертность будуt пропорциональна частоте контактов между особями (N^2).
Т.е. {смертность}= β*(N^2)(t), сл-но модель выглядит так: dN(t)/dt=λ*N(t)-β*(N^2)(t)
22. Детерминированные математические модели
детерминированные: модели, в которых абсолютно все известно
23. Два вида неопределенности. Примеры
стохастическая неопределенность может рассматриваться как случайная величина (пример: погода, спрос и т.д.)
полная определенность, напротив,- величина, к которой применение методов теории вероятности и мат статистики в принципе невозможно (любой результат в спорте)
24. Оптимизационные математически модели. Примеры
оптимизационные: описывают операции, в которых необходимо найти оптимальное и наилучшее решение
пример: любая ситуация, в которой есть цель и определенные ограничения (в ресурсах, объемах и т.д.)
25. Многокритериальные математические модели
Операции, характеризующиеся не одним, а сразу несколькими критериями
Пример: желание купить товар и покачественнее, и подешевле
Необходимыми для составления многокритериальной операции считаются: множество допустимых решений, множество критериев, сведения о предпочтениях ЛПР.
26. Математическое программирование
Предмет изучения – мат.модели, в которых ограничения, определяющие множество допустимых решений Х, ПРЕДСТАВЛЯЮТ СОБОЙ СИСТЕМУ РАВЕНСТ ИЛИ НЕРАВЕНСТВ.
Общий вид модели
1)х1,х2,х3….-возможные решения
2) F=F(х1,х2,х2…) max(min)
3) g1(x1,x2,x3…)>=,<=,= b1
………………………………………
gn(x1,x2,x3…)>=,<=,=bm
+ x1,x2,x3….>=0
После того, как решение модели найдено, можно считать такую модель задачей математического программирования.
В зависимости от вида ограничений и целевой функции бывают задачи линейного и нелинейного математического программирования.
27. Постановка общей задачи оптимизации
Общий вид модели
1)х1,х2,х3….-возможные решения
2) F=F(х1,х2,х2…) max(min)
3) g1(x1,x2,x3…)>=,<=,= b1
………………………………………
gn(x1,x2,x3…)>=,<=,=bm
+ x1,x2,x3….>=0
28. Задача о планировании производства.
1) x1,x2,…,xn-число едениц продукции, запланированной к производству
2)F(x)=pribyl’=c1*x1+c2*x2+…+cn*xnmax
3) {a11*x1+a12*x2+…+a1n*xn<=b1
…………………………………………………..ограничения по запасу ресурсов
am1*x1+am2*x2+…+amn*xn<=bm}
+ x1,…,n>=0
29. Задача о рационе
1)x1,x2,…,xn- кол-во продуктов, которое войдет в рацион
2) F(x)= стоимость рациона=c1*x1+c2*x2+…+cn*xnmin
3){a11*x1+a12*x2+…+a1n*xn>=b1
………………………………………………….. ограничения по кол-ву веществ в рационе
am1*x1+am2*x2+…+amn*xn>=bm}
30. Задача о раскрое