Глава 8. Цифровые схемы автоматики

8.1. Комбинационная логика

В устройствах автоматики с логическими входными сигналами часто необходимо вырабатывать определенные выходные сигналы для их передачи на последующие узлы. При этом различают два класса задач.

В задачах первого класса состояние выхода зависит от комбинации входных сигналов. Эти задачи называются комбинационными и решаются с помощью логических устройств, которые выполняют операции булевой алгебры в сисГлавах с двумя состояниями.

Другой класс задач требует не только формирования комбинации входных сигналов, но также знания их прежнего значения. Для решения таких задач применяют последовательные схемы (цифровые автоматы), имеющие в той или иной форме цифровую память.

Комбинационными устройствами называют логические устройства, не имеющие в своём составе запоминающих ячеек, при этом выходные сигналы зависят от входных, имеющих место только в данный момент времени.

Все цифровые устройства оперируют двоичными кодами, т.е. наборами нулей и единиц. Для описания цифровых устройств используется алгебра логики, в которой так же, как и в двоичном кодировании, переменные могут принимать только два значения: 0 или 1. В алгебре логики имеется три элементарных действия: дизъюнкция (ИЛИ), конъюнкция (И) и инверсия (НЕ).

Дизъюнкция, или логическое сложение, осуществляется по следующим правилам:

0 V 0 = 0,

0 V 1 = 1,

1 V 0 = 1,

1 V 1 = 1,

где V - знак операции дизъюнкции.

Можно также пользоваться знаком “+”, но в логических выражениях этот знак читается как ИЛИ. В дизъюнкции в отличие от двоичного кодирования при суммировании двух логических единиц переносов не осуществляется.

Конъюнкция, или логическое умножение, осуществляется по следующим правилам:

0  0 = 0,

0  1 = 0,

1  0 = 0,

1  1 = 1,

где  - знак операции конъюнкции. В логических выражениях допустимо также условное изображение операции конъюнкции отсутствием какого либо знака между переменными, записанными без пробела, однако читается это как И.

Инверсия представляет собой отрицание истины. Например, инверсия единицы есть нуль, а инверсия нуля есть единица. Операция инверсии обозначается прямой чертой над переменной:

(читается: не-икс, не-нуль, не-единица).

Законы алгебры логики представляют собой комбинации из дизъюнкций, конъюнкций и инверсий над логическими переменными. Возможные соотношения между ними приведены в таблице 8.1.

Законы отрицания в виде функций Пирса и Шеффера являются полными, т.е. посредством этих функций можно описать работу любого, сколь угодно сложного, логического устройства. Число различных логических функций от n переменных определяется соотношением: N =2²ⁿ.

8.2. Элементы комбинационных логических устройств

На рис.11.1а представлена схема ИЛИ, вы­полненная на диодах. Управляющий сигнал на выходе по­является при поступлении сигнала ИЛИ на один, ИЛИ на два других вхо­да, одновременно или вместе.

Таблица 8.1 – Основные законы алгебры логики

№	Название	Выражение
1.	Закон универсального множества	1VX1VX2VX3… VXn=1
2.	Закон нулевого множества	0X1X2X3… Xn=0
3.	Законы повторения	XVXVXVX… VX=X XXXX… X=X
4.	Закон многократной инверсии	и т.д.
5.	Переместительный закон	X1VX2=X2VX1, X1X2=X2X1
6.	Сочетательный закон	X1(X2X3)= (X1X2)X3= X2(X1X3)
7.	Законы дополнительности
8.	Распределительный закон	X1X2VX3= (X1VX2)(X2 VX3) X1VX2 X3= (X1X2)V(X2 X3)
9.	Законы поглощения	X1X1VX2= X1, X1X1X2= X1
10.	Законы склеивания	X1X2VX1 =X1 (X1X2)V( )=X1
11.	Законы отрицания: Пирса Шеффера

Сигнал той же полярности появляется на выходе схемы ИЛИ в том случае, когда хотя бы на одном из входов: - ИЛИ на U₁ ИЛИ на U₂ ИЛИ на U₃ будут логические сигналы (единицы).

На рис.8.1б приведена схема И, собранная на диодах. При поступлении сиг­нала только на один вход запирается соответствующий диод, а другие диоды остаются открытыми, в силу чего сопротивление между точками А и В остается малым и сигнал на выходе отсутствует. Таким образом, на выходе схемы И сигнал появится только тогда, когда на всех входах: И на U₁ И на U₂ И на U₃ будут логические сигналы (единицы).

Логическая схема НЕ выполняется на транзисторе (рис.8.1в), или инвертирующем операционном усилителе. На выходе этой схемы сигнал инверсный тому, который присутствует на входе. Если на входе присутствует логическая единица (высокий сигнал), то на выходе - логический нуль (низкий сигнал) и наоборот.

Р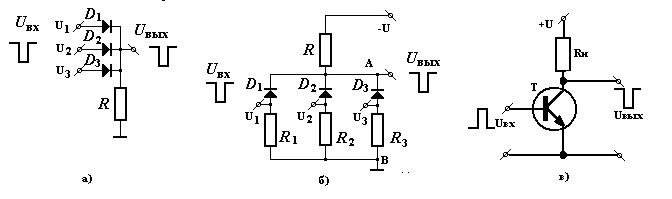 ассмотренные схемы на диодах имеют существенный недостаток, связанный с ослаблением сигнала при работе, что затрудняет осущест­вление каскадных соединений различных логических цепочек. От этого недостатка свободны схемы, дополненные транзисторами, выполняемыми по интегральным технологиям. Современная промышленность выпускает интегральные логические микросхемы с широкой гаммой логики.

Рисунок 8.1 – Исполнение логических элементов.

Для двух переменных имеют место 16 логических функций, математические соотношения и графические обозначения которых приведены в таблице 8.2.

Графическое изображение логических элементов осуществляется в виде прямоугольников, внутри которых ставятся условные символы:  - элементы с выполнением операции конъюнкции, 1 - элементы с выполнением операции дизъюнкции, =1 - исключающее ИЛИ.

С левой стороны прямоугольников изображают входы, а с правой - выходы (таблица 8.2). Входы или выходы, помеченные кружочками, соответствуют инвертированию сигнала. Входы или выходы, не несущие логической информации, например, входы расширения или питания, помечают крестиком х. На основе логических элементов может быть построена электронная схема любой сложности.

Таблица 8.2 – Некоторые функции двух переменных

Логическое выражение	Условное обозначение
Конъюнкция Z=XY
Исключающее ИЛИ Z=XY
Дизъюнкция Z=XVY
Функция Пирса
Логическая равнозначность
Инверсия
Функция Шеффера

Переключательной функцией в алгебре логики называют функцию, представляющую собой зависимость выходного сигнала от входных, имеющих место в данный момент времени. Для составления переключательных функций вначале составляют таблицы истинности (таблица 8.3). Столбцы в таблице истинности обозначают наименованиями входных и выходных переменных, а в строках записывают всевозможные сочетания входных и выходных сигналов в соответствии со словесным описанием алгоритма работы синтезируемых устройств.

Покажем это на примере мажоритарного элемента (рис.8.2), имеющего три входа X₁, X₂, X₃ и один выход Y. Единичный сигнал на выходе у такого элемента должен появится в том случае, если на двух или на трёх входах имеют место единичные сигналы. В противном случае на выходе должен быть нуль. Ниже представлена таблица истинности для мажоритарного элемента. На основании таблицы истинности переключательная функция может быть записана в следующем виде:

. (8.1)

Для построения мажоритарного элемента требуется: три инвертора для получения инверсных сигналов четыре трёхвходовых элемента 3И и один четырёхвходовый элемент 4ИЛИ (рис.8.2).

В большинстве случаев, применяя основные законы булевой алгебры, переключательные функции удаётся минимизировать, что в свою очередь снижает аппаратные затраты на построение устройств. Так, например, применяя закон дополнительности, формулу (8.1) можно привести к следующему, более простому, виду:

. (8.2)

Для построения того же мажоритарного элемента по формуле (8.2) требуется всего три двухвходовых элемента 2И и один трёхвходовый элемент 3ИЛИ.

Минимизация логических функций осуществляется с целью снижения аппаратных затрат при построении комбинационных устройств. Основными критериями при минимизации являются: сокращение числа членов в переключательной функции, числа входов у используемых логических элементов, числа межсхемных соединений, а также числа логических операций, необходимых для выполнения функции. При минимизации результирующее действие переключательных функций сохраняется постоянным. Для целей минимизации переключательных функций, имеющих до трёх переменных, используют аналитические методы с применением основных законов алгебры логики.

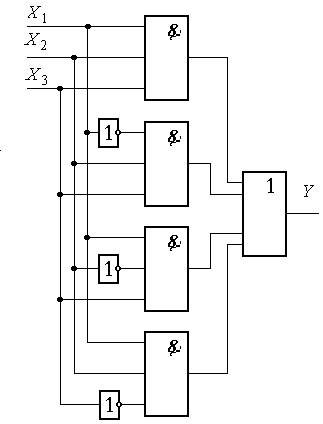
Таблица 8.3 – Таблица истинности

для мажоритарного элемента

X1	X2	X3	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Рисунок 8.2 – Мажиротарный элемент