4.2.4. Инерционные звенья второго порядка

 Уравнение инерционного звена второго порядка:

T₁²p²y + T₂py + y = ku.

Передаточная функция: W(p) = .

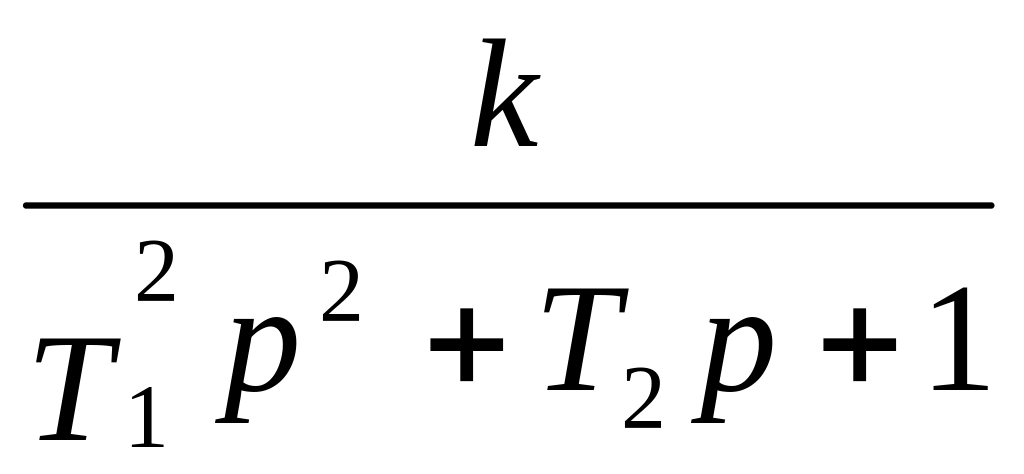Решение уравнения зависит от соотношения постоянных времени T₁ и T₂, которое определяет коэффициент затухания

r = .

Можно записать W(p) = ,

где T = T₁.

Если r ≥ 1, то знаменатель W(p) имеет два вещественных корня p₁ и p₂ и раскладывается на два сомножителя:

T₂p₂ + 2rTp + 1 = T₂ (p - p₁)(p - p₂).

Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.

Р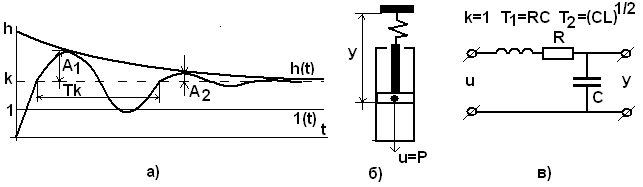 исунок 4.7 – Переходная характеристика инерционного звена

второго порядка: А₁; А₂ – амплитуда колебаний в разное время t; Т_к – период колебаний; 1(t) – единичная функция; h(t) – переходная характеристика.

При r<1 корни полинома знаменателя W(p) комплексно сопряженные:

p_1,2 = α ± j ω.

Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс (рис.4.7а), с затуханием α и частотой ω (рис.4.7). Такое звено называется колебательным.

При r = 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называется консервативным.

Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство (рис.4.7б), электрический колебательный контур с активным сопротивлением (рис.4.7в) и т.п. Зная характеристики реального устройства можно, определить его параметры как колебательного звена. Передаточный коэффициент k равен установившемуся значению переходной функции.

 

4.2.5. Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена:

y(t) = , или y = kpu.

Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция:

W(p) = kp.

При k=1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика:

h(t) = k 1'(t) = d(t).

Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его уравнение:

T p y + y = k T p u.

Передаточная функция:

W(p) = .

При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристику можно вывести с помощью формулы Хевисайда:

,

здесь p₁=-1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D'(p₁) = T.

По переходной характеристике, имеющей вид экспоненты (рис.4.8а), можно определить передаточный коэффициент k  и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости (рис.4.8б) и демпфер, (рис.4.8.в). Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.

При подаче на вход единичного ступенчатого воздействия выход оказывается ограничен по величине и растянут во времени (рис.4.8а).

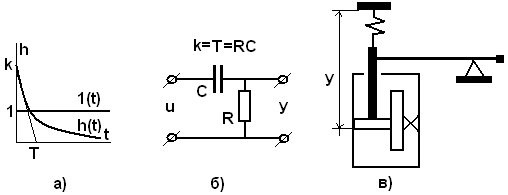
Рисунок 4.8 – Разновидность типовых дифференцирующих звеньев САР.