111. Резольвента – это

 дизъюнкт, полученный в результате соединения двух дизъюнктов, в один из которых входит некоторая литера без отрицания, а в другой – с отрицанием.

 дизъюнкт, полученный в результате удаления из него некоторой литеры с отрицанием и без отрицания.

 дизъюнкт, полученный в результате сколемизации, т.е. удаления всех -квантифицированных переменных.

112. Главная идея метода резолюций состоит

 в доказательстве совместной невыполнимости множества аксиом A_i и отрицания целевого утверждения F, т.е. невыполнимости формулы

 в доказательстве "от противного": для доказательства выводимости формулы из набора аксиом к набору добавляется отрицание исследуемой формулы, и осуществляется попытка вывести противоречие.

 в доказательстве выводимости формулы из набора аксиом путём применения правил вывода (законов логики высказывания или логики предикатов) к ДНФ-формам этих аксиом.

 в доказательстве выводимости формулы из набора аксиом путём применения правил вывода (законов логики высказывания или логики предикатов) к КНФ-формам этих аксиом.

113. Метод резолюций

 выдает ответ «Да», если F является логическим следствием из множества аксиом {А₁, А₂, …А_n}.

 выдает ответ «Нет» если не верно, что F является логическим следствием из множества аксиом {А₁, А₂, …А_n}.

 не выдает никакого ответа (то есть зацикливается), если неверно, что F является логическим следствием из множества аксиом {А₁, А₂, …А_n}.

 выдает ответ «Да», если F является логическим следствием из множества {А₁& А₂& …&А_n F}.

 выдает ответ «Нет» если не верно, что F является логическим следствием из множества {А₁& А₂& …&А_n F}.

 не выдает никакого ответа (то есть зацикливается), если неверно, что F является логическим следствием из множества аксиом {А₁& А₂& …&А_n F}.

114. Метод резолюций

 выдаёт один из ответов "да" или "нет".

 может привести к комбинаторному взрыву.

 может выдать несколько ответов "да" и только один ответ "нет".

 может выдать только один ответ "да" и несколько ответов "нет".

 либо выдаёт ответ "да" , либо приводит к комбинаторному взрыву.

115. В основе автоматического доказательства теорем логики предикатов и логики высказываний лежит

 метод резолюции.

 метод сколемизации.

 автоматическое применение логических законов (правил вывода).

 поэтапное исключения кванторов и метод выбора наименьшего унификатора.

Модуль 2 элементы теории графов

116. Назовите алгоритм нахождения кратчайшего пути от узла-источника ко всем другим узлам

 алгоритм Дейкстры.

 алгоритм Беллмана-Форда.

 алгоритм Флойда-Уоршела.

117. Теория графов ‑

 раздел математики, основная особенность которого заключается в геометрическом подходе к изучению объектов.

 раздел математики, в котором изучаются общие свойства графических систем.

 раздел математики, в котором изучаются свойства и характеристики геометрических объектов.

 раздел математики, в котором изучаются свойства и характеристики структурных объектов.

118. Ребра графа называются смежными, если они

 инцидентны одной и той же вершине.

 параллельны.

 являются кратными.

119. Граф задаётся

 множеством вершин (точек) и множеством ребер (связей), соединяющих некоторые пары вершин.

 матрицей смежности.

 матрицей дуг.

 списками вершин.

120. Если две вершины соединены одной дугой, они называются

 смежными.

 коинцидентными.

 инцидентными

121. Какие из графов я.вляются подграфами данного графа G

   

122. Если любые две вершины графа можно соединить простой цепью, то граф называется:

 связным

 деревом

 несвязным

 остовом

123. Для графа, представленного на рисунке, матрица смежности имеет вид

  

124. Для графа, представленного на рисунке, матрица инциденций имеет вид

  

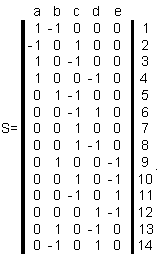
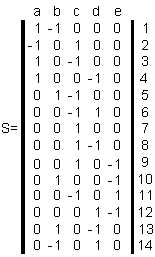
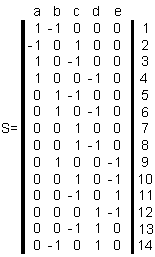
125. Равны ли графы? 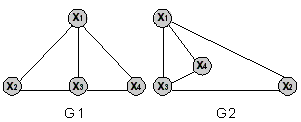(проверить по матрице смежности)

 да

 нет

126. Даны графы





127. Даны графы





128. Даны графы





129. Квадрат G² графа G

  

130. Квадрат G² графа G

  

131. Эйлеров цикл графа

 (1, 2, 3, 4, 5, 6, 7, 8, 9)

 (1, 2, , 6, 7, 8, 9)

 (1, 2, 3, 4, 6, 5, 7, 8, 9)

 (1, 9, 8, 7, 6, 5, 4, 2,3)

132. Граф является эйлеровым тогда и только тогда,

 когда он связен и степень каждой вершины чётна.

 когда он связен, а степень каждой вершины не важна

 когда он связен и степень каждой вершины нечётна

133. Граф является

 неэйлеровым

 несвязным

 эйлеровым

 связным

134. Граф является

 эйлеровым

 связным

 неэйлеровым

 несвязным

135. Сколько вершин содержит гамильтонов цикл графа с 5 вершинами?

 5

 4

 6

136. Граф содержит 7 дуг. Его эйлеров цикл будет состоять из

 7 дуг

 6 дуг

 8 дуг

137. Эйлеров цикл

 содержит каждое ребро только один раз.

 содержит каждую вершину только один раз.

 проходит через все вершины и ребра графа только один раз.

138. Гамильтонов цикл

 содержит каждую вершину только один раз.

 содержит каждое ребро только один раз.

 проходит через все вершины и ребра графа только один раз.

139. В эйлеровом графе все вершины

 четной степени.

 нечетной степени.

140. В эйлеровом графе допускаются

 2 вершины нечетной степени.

 3 вершины нечетной степени.

 1 вершина нечетной степени.

141. Какой алгоритм определяет гамильтоновы циклы графа:

 Гильберта-Мура

 Флери

 Робертса-Флореса

 Дейкстры

142. Какой из циклов графа с множеством вершин {a,b,c,d,e,f} является гамильтоновым?

 abecdfa

 abeca

 fbecdf

 abcdfca

143. Двоичным деревом называется

 ориентированное дерево, полустепень числа исходящих дуг из исхода каждой вершины которого не превышает 2.

 неориентированное дерево, полустепень числа исходящих дуг из исхода каждой вершины которого не превышает 2.

 ориентированное дерево, полустепень числа исходящих дуг из исхода каждой вершины которого не превышает 2².

 неориентированное дерево, полустепень числа исходящих дуг из исхода каждой вершины которого не превышает 2²

144. На рисунке представлено

 дерево

 двоичное дерево

 сеть

 двоичная сеть

145. Длина ориентированного пути в графе G – это

 сумма длин рёбер, входящих в путь.

 сумма длин рёбер графа.

 сумма длин рёбер графа минус сумма длин рёбер, входящих в путь.

146. Кратчайшим путем из вершины s в вершину t называется

 ориентированный s-t – путь, имеющий минимальную длину.

 ориентированный s-t – путь, не имеющий промежуточных вершин .

147. Расстоянием от вершины s до вершины t d(s, t) называется

 длина кратчайшего ориентированного s-t пути.

 эвклидово расстояние между s и t, вычисленное в эвклидовом пространстве.

 хэммингово расстояние между s и t, вычисленное в эвклидовом пространстве.

148. Алгоритм Дейкстры

 определяет кратчайшие пути из данной вершины ко всем другим вершинам связного (в общем случае ориентированного) ориентированного графа, состоящего из n вершин.

 построение остова наименьшей длины.

 построение кратчайшего пути из одной вершины в другую.

149. Алгоритм Краскала осуществялет:

 построение кратчайшего остова.

 построение оптимального дерева бинарного поиска.

 построение дерева кратчайших путей.

150. В графе из n вершин остов содержит:

 n-1 ребро

 n ребер

 2n ребер

 n+1 ребро

151. Дерево есть:

 связный граф без циклов.

 остовный подграф графа.

 граф без циклов.

 связный граф.

152. Простая цепь это:

 маршрут, где нет повторяющихся вершин и ребер.

 маршрут, где нет повторяющихся ребер.

 маршрут, где нет повторяющихся вершин.

 маршрут минимальной стоимости.

153. Расстояние между вершинами есть

 длина кратчайшего пути.

 сумма длин ребер, входящих в путь.

154. Глубина элемента а2 в дереве равна

 1

 0

 2

 3

155. Степень вершины а2 в графе равна

 3

 0

 1

 2