Алгебры и алгебраические структуры. Булева алгебра.

61. Решетка –

 частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет точную верхнюю (sup) и точную нижнюю (inf) грани.

 алгебраическая система , любые два элемента которой имеют единственные точные верхнюю и нижнюю грани, определяемые следующим образом: .

 упорядоченное множество, в котором двухэлементные подмножества не равны между собой.

 множество, в котором есть минимальный (inf – infinum) и максимальный элементы (sup – supremum).

62. Решёткой является

 универсальная алгебра с двумя бинарными операциями , удовлетворяющими свойствам: идемпотентности, коммутативности, ассоциативности, поглощения.

 универсальная алгебра с двумя бинарными операциями , удовлетворяющими свойствам: дистрибутивности, коммутативности, ассоциативности, отрицания.

63. Решёткой является

 любое линейно упорядоченное множество.

 множество всех подмножеств данного множества (булеан), упорядоченное по включению.

 счётное множество.

 несчётное множество.

 бесконечное множество.

 конечное множество.

64. Решетка называется дедекиндовой (модулярной) тогда и только тогда, когда для любых ее трех элементов выполнено условие:







65. Решетка называется дистрибутивной, если для любых её трех элементов ( 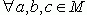) выполнены тождества:

 ,



66. Булеву алгебру можно рассматривать

 как дистрибутивную решетку с дополнениями.

 как декиндову решётку.

 как дистрибутивную решётку.

 как подрешётку классической алгебры.

67. Какой из законов не обязательно присутствует в определении решетки:

 дистрибутивный.

 коммутативный.

 элиминации.

 ассоциативный.

68. Какой закон в дополнение к обязательным определяет решетку как булеву алгебру:

 дистрибутивный.

 коммутативный.

 элиминации.

 ассоциативный.

69. Решетка определяется на:

 частично упорядоченном множестве.

 произвольном множестве.

 линейно упорядоченном множестве.

 неупорядоченном множестве.

70. Какое из условий определяет дедекиндову решетку:















71. Какое из условий определяет дистрибутивную решетку в дополнение к свойству модулярности:













72. Абстрактная алгебра

 раздел математики, изучающий алгебраические системы (также иногда называемые алгебраическими структурами), такие как группы, кольца, поля, частично упорядоченные множества, решётки, а также отображения между такими структурами.

 это непустая система подмножеств, замкнутая относительно дополнения и объединения.

 совокупность вещественных чисел с определёнными для них операциями сложения и умножения являются алгеброй.

73. Раздел математики, изучающий алгебраические системы, такие как группы, кольца, поля, частично упорядоченные множества, решётки, а также отображения между такими структурами, называется

 абстрактной алгеброй.

 теоретической алгеброй.

 высшей алгеброй.

 алгеброй множеств.

74. Булево выражение называется выполнимым,

 если существует хотя бы одна комбинация значений переменных, подстановка которых обращает его в единицу.

 если его можно привести к КНФ.

 если его можно привести к ДНФ.

 если оно допускает построение эквивалентного отрицаня

75. Сколько двоичных наборов содержит таблица истинности функции f(a,b,c)?

 8

 2

 3

 7

76. Чему равно логическое выражение ?





 0

 1

77. Предельное дизъюнктивное разложение функции по теореме Шеннона есть

 СДНФ

 СКНФ

 ДНФ

 КНФ

78. На каком входном наборе дизъюнкция двух переменных равна единице?

 0 1

 1 0

 1 1

 0 0

79. Функция f(x1,x2,...,xn) называется булевой, если каждый ее аргумент и сама функция суть булевы переменные

 если каждый ее аргумент и сама функция суть булевы переменные.

 если каждый ее аргумент является булевой переменной.

 если каждый ее аргумент принимает значения {1, 0}.

80. На каком входном наборе конъюнкция двух переменных равна нулю?

 0 1

 1 0

 0 0

 1 1

81. Конъюнкция некоторого числа переменных равна единице, когда

 все переменные равны единице.

 все переменные равны нулю.

 хотя бы одна переменная равна единице.

 хотя бы одна переменная равна нулю.

82. Дизъюнкция некоторого числа переменных равна единице, когда

 все переменные равны единице;

 хотя бы одна переменная равна единице;

 хотя бы одна переменная равна нулю.

83. Бyлевыми фyнкциями (истинностными фyнкциями) называются

 функции, определенные на множестве состоящем из двух элементов {0, 1} и принимающие значения тоже на этом множестве.

 функции, определенные на множестве состоящем из двух элементов {0, 1}.

 принимающие значения на множестве из двух элементов {0, 1}.

84. Областью определения булевой функции является

 множество, состоящее из нуля и единицы.

 множество всех булевых констант.

 множество натуральных чисел.

 множество действительных чисел.

 множество комплексных чисел.

85. Каждая функция из множества всех булевых функций является сyпеpпозицией следующих функций:

 отрицание, конъюнкция, дизъюнкция.

 отрицание, конъюнкция.

 отрицание, дизъюнкция.

 конъюнкция, дизъюнкция.

86. Булевы функции называются равными,

 если на одинаковых наборах они принимают одинаковые значения.

 если на каждом наборе значений аргументов x₁, x₂, ..., x_n функции f₁(x₁,x₂,...,x_n) и f₂(x₁,x₂,...,x_n) принимают одно и то же значение.

 если совпадают их таблицы истинности.

 если число входящих в них переменных равны.

 если число входящих в них переменных и значения этих переменных равны.

87. Разложение булевой функции f(x1,x2,...,xn) по переменной xi производится

 по формуле Шеннона: .

 по формуле Шеннона f(x₁,x₂,...,x_n)= x₁f(1,x₂,...,x_n)+ х₁(0,x₂,...,x_n) +…+ x_nf(1,x₂,...,x_n)+ х_n(0,x₂,...,x_n).

 по формуле Шеннона f(x₁,x₂,...,x_n)= x₁f(1,x₂,...,x_n)+…+ x_nf(1,x₂,...,x_n).

 по формуле Шеннона f(x₁,x₂,...,x_n)= x₁f(1,x₂,...,x_n)… x_nf(1,x₂,...,x_n).

 по формуле Шеннона f(x₁,x₂,...,x_n)= x₁f(1,x₂,...,x_n)… x_nf(1,x₂,...,x_n).

88. К элементарным функциям относятся

 не зависящие от аргументов: константа 0 и константа 1;

 одного аргумента: тождественная функция f(x) = x и функция отрицания f(x) = , которая называется инверсией или функцией НЕ.

 функции двух аргументов: конъюнкция, дизъюнкция, импликация

89. ДHФ, задающая бyлевy функцию f называется минимальной ДHФ функции f, если она

 содержит наименьшее число букв по сравнению со всеми другими ДHФ, задающими данную функцию.

 содержит только положительные литеры, т.е. буквы без отрицания.

 содержит минимальное число отрицательных литер, т.е.букв с отрицанием.

90. Таблицей истинности называется таблица, которая содержит

 все наборы значений аргументов, упорядоченные по возрастанию значений чисел, и соответствующие им значения булевой функции.

 такие наборы значений аргументов, при которых соответствующие им значения булевой функции являются истинными