Даны множества
Взаимно однозначное соответствие ‑
такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определенный элемент второго множества, а каждому элементу второго множества - один определенный элемент первого множества
такое соответствие между элементами двух множеств, при котором каждый элемент первого множества равен значению некоторой функции f, тогда как соответствующий элемент второго множества соответственно равен значению функции g. Причём функции f и g взаимнообратны.
Заданы множества A={2,4,3,1} и B={4,2,1,3}, тогда для них неверным утверждением будет…
множество A включает в себя множество B.
множества A и B равны .
множества A и B не имеют общих элементов.
множество A есть подмножество множества B .
Заданы множества M={2, 3, 4, 5} и N={4, 3}, тогда для них верным утверждением будет…
множества M и N равны.
множества M и N не имеют общих элементов.
множества M включает в себя множество N.
множество M есть подмножество множества N.
Заданы множества A={1,2,3} и B={1,2,3,4,5}, тогда для них верным утверждением будет…
множество A есть подмножество множества B.
множества A и B равны.
множества A и B не имеют общих элементов.
множество A включает в себя множество B.
Заданы множества A={2,3,4,5} и D={5,2,3}, тогда для них верным утверждением будет…
множество D есть подмножество множества A.
множество A включает в себя множество D.
множества D и A состоят из одинаковых элементов.
множества A и D равны.
Заданы множества A={1,2,3} и M={2,3}, тогда для них верным утверждением будет…
множества M включает в себя множество A
множество M есть подмножество множества A
множества A и M равны
множество A есть подмножество множества M
Выбрать верный порядок убывания старшинства операций алгебры Кантора
Выбрать формулу, соответствующую дистрибутивному закону
Указать формулу, соответствующую закону Порецкого
Могут ли повторяться элементы множества?
нет
да
при определённых условиях - да
Является ли множество несобственным подмножеством самого себя?
да
нет
да, при определённых условиях
Множества равны, если они содержат:
одинаковые элементы.
одинаковое количество элементов.
Являются ли понятия мощности множества и его кардинального числа идентичными?
да
нет
да при определённых условиях
Булеан множества А={{1, 2}, 3} определяется как
Какое из утверждений верно для всех множеств А,В,С:
Какой закон определяется формулой
?
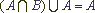элиминации.
Порецкого
Де Моргана
инволюции
Чему равно выражение
?
А
В
два подхода к теории множеств
наивная теория множеств Кантора.
аксиоматическая теория множеств.
алгебраическая теория множеств.
математическая теория множеств.
графо-аналитическая теория множеств.
Диаграммы Эйлера ‑ Венна
содержат результаты операций над геометрическими фигурами как множествами точек
представляют собой визуальное представление множеств
определяют порядок сравнения множеств