2.2. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины Х по абсолютной величине меньше заданного положительного числа , т. е. требуется найти вероятность осуществления неравенства  |x —а|<.

Заменим это неравенство равносильным ему двойным неравенством

Тогда получим:

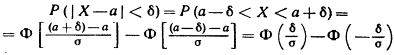
Приняв во внимание равенство:

(функция Лапласа—нечетная), окончательно имеем

 Вероятность заданного отклонения равна

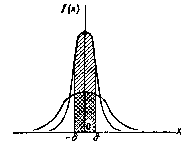
На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-,),больше у той величины, которая имеет меньшее значение . Этот факт полностью соответствует вероятностному смыслу параметра  .

Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение: Воспользуемся формулой

  

 По условию ,

тогда

2.3. Правило трех сигм

                               

Преобразуем формулу   

     

Введем обозначение

Тогда получим:

  

Если t=3, то

т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна  0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:

 Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

3. Показательное распределение.

3.1. Интегральная и дифференциальная функции распределения.

 Определение: Непрерывная случайная величина X, функция плотности которой задается выражением

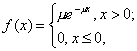
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.

Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.

Как видно из формулы , показательное распределение определяется только одним параметром .

Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения:

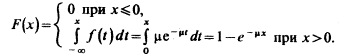
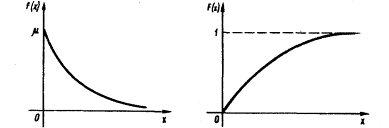
Графики дифференциальной и интегральной функций показательного распределения имеют вид: