9. Цикл Карно.

Цикл Карно – это обратимый цикл, состоящий из 2-ух изотерм и двух адиабат .

ηt= 1- = 1- T2/T1 = ηtk. 1 теор. Карно –эффективность цикла

Карно не зависит от свойств рабочего тела, а определяется только уровнем

Температуры горячего и холодного источников. Так как цикл Карно

обратимый, темп. Т1 = Тг , а Т2 = Тх

2 теор. Карно в заданном диапазоне температур холодного и горячего источника

мах. КПД имеет цикл Карно, работающий в этом диапазоне.

Рассмотрим цикл Карно 1234, работающий в диапазоне горячего и холодного

источника ηt (ABCD)<ηt (abcd) = 1- , ηt (1234)= 1-(Tx/Tr), Tx≤T2m, Tr≥T1m

• ηt (1234)≥ ηt(ABCD) . Выше рассмотрены прямые циклы, все это справедливо и для обратного. Но для обратного цикла Карно холодильный коэф.εк =

Для отопительного коэф. φк = . Цикл Карно идеальный в лбом случае.

10.Эквивалентный цикл Карно.

Любой произвольный цикл АВСД, в котором подвод и отвод теплоты происходит при переменных температурах , можно заменить эквивалентным циклом Карно 1234, где q1, q2 и изменение удельной энтропии s2 – s1 соответствуют таковым в цикле АВСД .С учетом того, что

q1 = qABC = (ABC)∫ Tds = T 1 cp(s2-s1), q2= qCDA = (CDA)∫Tds = T2 cp (s2-s1). Термический КПД произвольного цикла запишем так:

ηt ABCD = 1- q2/q1 = 1- , где Т2ср и Т1ср – средние ТД температуры, соответствующая процессам подвода и отвода теплоты: Т1ср = ; T2cp = и определяются как высоты прямоугольников , одинаковых по площадям с фигурами s1ABCs2 и s2CDAs1. Для повышения термического КПД любого цикла тепловых двигателей необходимо увеличивать среднюю темп. в процессе подвода теплоты(Т1ср) и уменьшать среднюю темп. в процессе отвода теплоты (Т2ср). Пределом терм. КПД произвольного цикла, осуществляемого между крайними температурами Т мах и Т міn является терм. КПД цикла Карно при Т1ср = Тмах и Т2ср = Тміn, следовательно в данном интервале температур цикл Карно обладает наибольшей эффективностью .

11) Изобарный процесс : ( р=const )

В р-V координатах графикпроцессаизображаетсягоризонтальнойпрямой 1-2:

Рис. График ізобарного процесса с идиальным газом в pV-координатах.

Записав уровнения состояния для двух точек процесса зависимость между изеняющиемися параметрами идеального газа в изобарном процессе: V2/V1=T2/T1.

Измененияудельнойвнутренийєнергииидеального газа определяется выражениям

). Удельнаяработа , выполняемая в изобарном процессе:

Так как для идеального газа pV₂=RT₂и pV₁=RT₁ , то .

Если в изобарном процессе температура 1кг идеального газа изменится на 1К, то , т.е удельная газовая постоянная – эта работа, совершаемая 1кг идеального газа в изобарном процессе при изменении его температуры на 1К. Удельное количество теплоты можно определить: , т.е. удельное количество теплоты в изобарном процессе равно изменению удельной энтальпии идеального газа. Для идеального газа:

Выражения для расчета изменения удельной энтропии идеального газа в изобарном процессе можно получить: или .

Следовательно, на TS-диаграмме изобара является также логарифмической кривой.

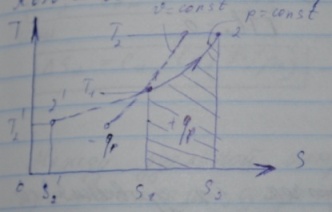
Так какС_р>С_V, то следует что изобара более пологая, чем изохора.

Доля удельной теплоты, расходуемой на изменения удельной внутренней энергии идеального газа в изобарном процессе, 1/k, т.е. изобарный процес этотакойпроцесс, в котором 1/К

Доля удельнойтеплотырасходуется на изменениеудельнойвнутреннейэнергииидеального газа.

12)Изохорный процесс ( V=const). ВpV-координатах график процесса представляет собой прямую линию, паралельную оси Op. Процесс может протекать как с повышением лавления( прямая 1-2 , так и с его понижением ( прямая 1-2^’).

Записав для крайних точек 1,2 уравнения состояния и разделив их почленно, получим зависимости

между параметрами идеального газа в изохорном процессе:

p₁V=RT₁,p₂V=RT₂илиp₂/p₁=T₂/T₁.

В изохорном процессе dV=o и термодинамическая работа не совершается ( =o). Потому вся теплота расходуется только на изменение внутренней энергии идеального газа.

Q_V=

Выражения для расчета изменения удельной энтропии идеального газа в изохорном процессе можно получить на основании S=S₂-S₁=C_vmln(T₂/T₁) + Rln( V₂/V₁) , положив V₁=V₂: S_V=C_Vmln(T₂/T₁)

или S_V=C_Vmln(p₂/p₁).

Между удельной энтропией и температурой идеального газа существует логарифмическая зависимость. BTs-координатах эта зависимость изображается кривой 1-2:

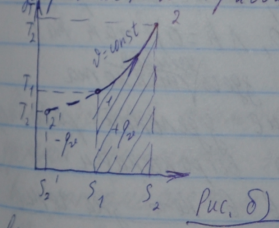
Схема энергетического баланса для изохорного процесса показана на рис. а). Доля удельной теплоты,

расходуемой на изменение удельной энергии идеального газа: , поскольку q_V= U_V.

13) Изотермический процесс ( T=const ):

Уравнение процесса вытикает из уравнения состояния идеального газа: pV=RT=const.

НаpV-диаграммеизотерма изображается равнобокой гиперболой:

Между давлением и обьемом существует обратно пропорциональная зависимость.

Удельны внутренняя энергия и энтальпия идеального газа в изотермическом процессе не изменяются ( U=0, =0), так как dT=0. Вся подведенная здесь удельная теплота расходуется определяется выражениям:

Удельная теплота, необходимая для осуществления процесса:

q₁=l_T=RTln(V2/V1)=RTln(p1/p2)

или

q_T=T(S2₂-S₁)

Выражения для расчета изменения удельной энтропии идеального газа в изотерм., процесса:

S_T=S₂-S₁=q₁/T=Rln(V2/V1)=Rln(p1/p2)

График изотермического процесса в Ts-координатах:

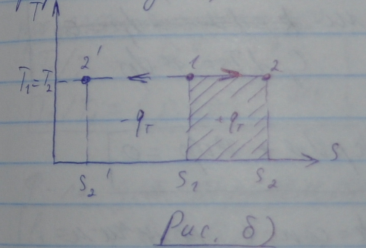
Доля удельной теплоты, расходуемой на изменение удельной внутренней энергии идеального газа в изотермическом процессе: .