Принцип Даламбера и метод кинетостатики

1. Основные понятия и определения

Принцип Даламбера: Для несвободной движущейся механической системы в любой момент времени геометрическая сумма главных векторов внешних сил, сил реакций связей и сил инерции, а также геометрическая сумма главных моментов этих сил относительно неподвижного центра равны нулю.

1.1. Силы инерции. Определение сил инерции в различных случаях движения твердого тела

Для несвободной механической системы главные вектор и момент сил инерции определяются из основных теорем динамики системы и являются основой для приведения сил инерции, приложенных к твердому телу, к простейшему виду. Простейший вид зависит от вида движения твердого тела.

1. Поступательное движение твердого тела.

В этом случае силы инерции приводятся к равнодействующей , приложенной в центре масс тела.

,

(1.1)

где М – масса тела, - ускорение центра масс тела. Знак « – » означает, что сила направлена в сторону, противоположную ускорению .

2. Вращение тела вокруг неподвижной оси, проходящей через центр масс тела.

Если тело вращается вокруг главной центральной оси инерции (например ось Z), то силы инерции приводятся к паре сил инерции,

,

(1.2)

где - осевой момент инерции тела, - угловое ускорение. Знак «– » показывает, что пара направлена против направления .

­

3. Плоское движение тела.

При плоском движении силы инерции приводятся к силе инерции приложенной в центре масс тела, и паре сил инерции относительно оси, перпендикулярной плоскости движения и проходящей церез центр масс

, ,

(1.3)

где - осевой момент инерции относительно оси , перпендикулярной плоскости движения и проходящей через центр масс тела, - угловое ускорение тела вокруг этой оси. Знак « – » показывает, что и направлены в стороны, противоположные и соответственно.

1.2. Метод кинетостатики

Методом кинетостатики называется искусственный прием, позволяющий записать уравнения движения в виде уравнений статики, основанный на принципе Даламбера.

Если система состоит из нескольких тел, то к каждому телу, помимо активных сил и сил реакций связей, прикладываются соответствующие силы инерции, после чего составляются уравнения равновесия.

При решении задач методом кинетостатики рекомендуется следующая последовательность действий:

1) Выбрать систему, «движение» которой рассматривается, определить вид движения каждого из тел системы;

2) Выбрать систему координат;

3) Составить уравнения равновесия для каждого из тел системы, предварительно расчленив систему по внутренним связям на отдельные тела, где это необходимо;

4) Решить уравнения равновесия и исследовать ответ.

Расчленять систему целесообразно, если она состоит из нескольких тел, и когда вычисление сил инерции вызывает затруднения.

1.3. Пример решения задачи

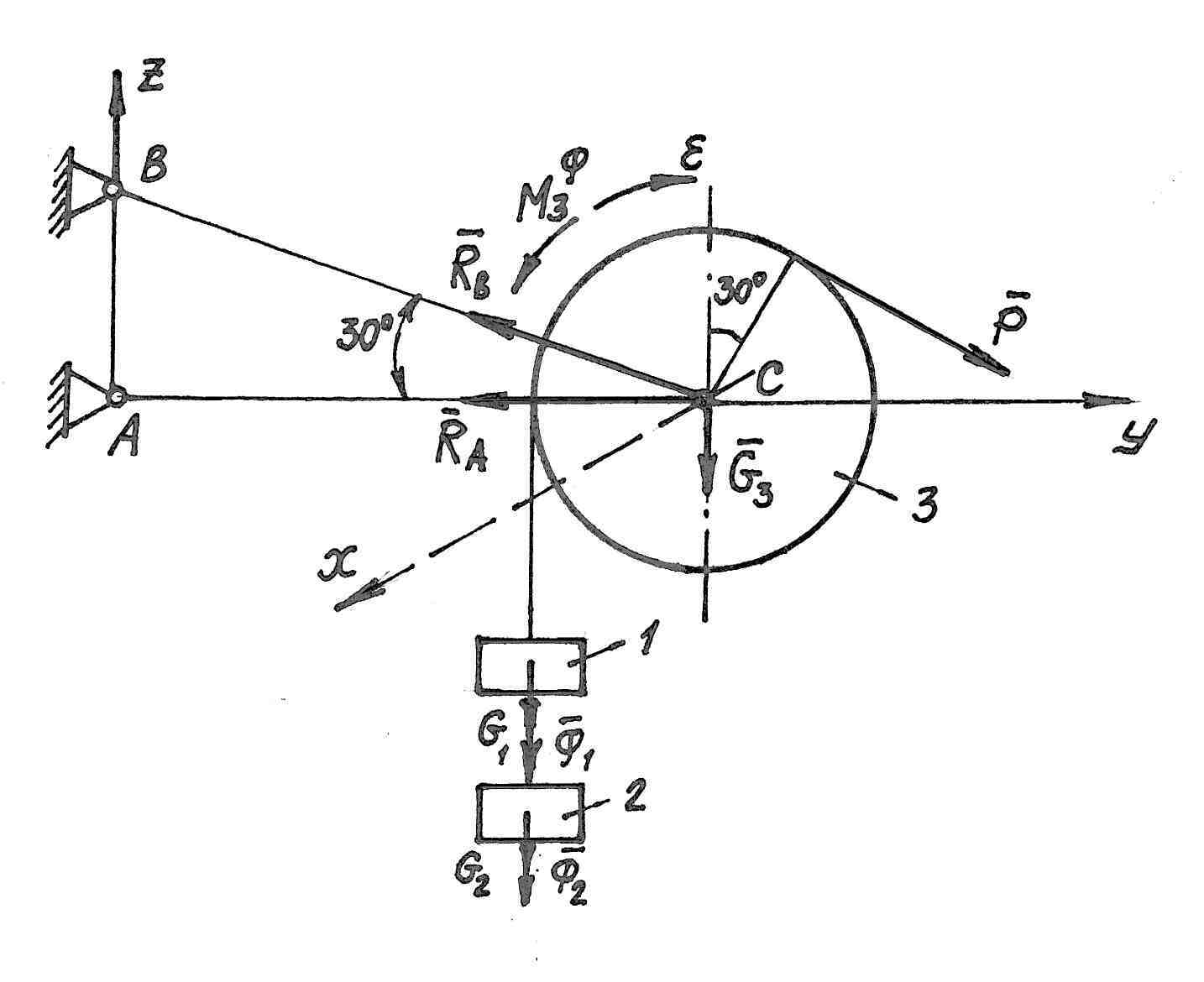
Однородный барабан массы М₃ и радиуса R присоединен шарнирно двумя ненагруженными стержнями АС и ВС к стене. На барабан намотана невесомая нерастяжимая нить, к одному концу которой присоединены два груза, массами М₁ и М₂ соответственно, соединенные нитью, а на другой конец действует постоянная сила Р. Найти усилия в стержных АС и ВС.

Рассмотрим систему тел 1, 2 и 3. Тела 1 и 2 совершают поступательное движение, тело 3 вращается вокруг оси , проходящей через точку С.

Выберем систему координат

Активными силами будут: . Реакции связей и направлены вдоль стержней, которые считаем растянутыми.

Приложим соответствующие силы инерции

и . При этом считаем, что тело 3 вращается в сторону, определяемую направлением силы .

Составим уравнения равновесия

	(1.4)

Решая эту систему, получим

	(1.5)
	(1.6)

Для отыскания значений сил инерции и , составим уравнение моментов относительно точки и приравняем его нулю.

.	(1.7)

Из кинематики известно, что

,

(1.8)

откуда, после дифференцирования, получаем

(1.9)

Подставим (1.9) в (1.7), получим

(1.10)

Из (1.10) находим

(1.11)

Находим соответствующие силы инерции

(1.12)

Подставляя значения и в (1.5) и (1.6) определим значения реакций связей:

Оценивая полученные значения, можно предположить, что стержень ВС растянут, а стержень АС – сжат.