4. Теорема об изменении кинетического момента механической системы
Производная по времени от кинетического момента системы материальных точек относительно неподвижного центра равна геометрической сумме моментов всех внешних сил относительно того же центра:
.
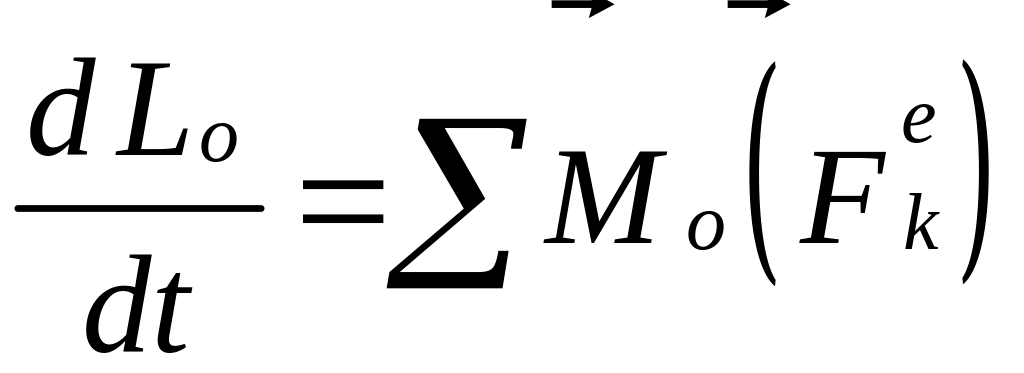В проекциях на оси декартовых координат указанное равенство эквивалентно скалярным равенствам:
.
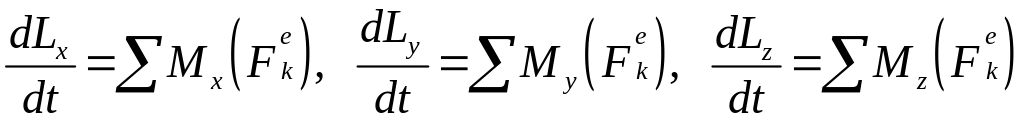Посредством теоремы могут быть решены прямые и обратные задачи динамики. Теорему удобно применять при рассмотрении движения системы, в состав которой входят тела, вращающиеся вокруг неподвижной оси.
Закон сохранения кинетического момента:
1. Если геометрическая сумма моментов всех внешних сил относительно неподвижного центра равна нулю, то кинетический момент системы относительно того же центра постоянен:
.
2. Если алгебраическая сумма моментов всех внешних сил системы относительно неподвижной оси равна нулю, то проекция кинетического момента на эту ось есть величина постоянная:
.
Рекомендуемая при решении задач последовательность действий:
1) дать анализ движения тел, входящих в изучаемую механическую систему;
2) направить одну из осей координат вдоль неподвижной оси вращения;
3) записать теорему об изменении кинетического момента системы относительно соответствующей оси;
4) изобразить на схеме все внешние силы системы (активные и реакции внешних связей);
5) вычислить главный момент количеств движения системы относительно неподвижной оси, затем его производную по времени;
6) в зависимости от условий решить прямую или обратную задачу динамики.
При выполнении закона сохранения кинетического момент необходимо: к п.п. 1) – 4):
а) показать, что сумма моментов внешних сил системы относительно оси равна нулю;
б) вычислить и приравнять к нулю кинетические моменты системы относительно оси в начальный и конечный моменты времени.
в) решить уравнение
и найти искомую величину.
4.1. Применение теоремы об изменении кинетического момента механической системы к решению задач
Пример 1
Маховик,
момент инерции которого I,
в начале торможения имел угловую скорость
.
Определить, через сколько времени его угловая скорость уменьшится в два раза, если момент сил сопротивления пропорционален квадрату угловой скорости (коэффициент пропорциональности равен k).
Решение:
1) Механическая система состоит из одного твёрдого тела, вращающегося вокруг неподвижной оси.
2) Так как сила тяжести маховика и сила реакции со стороны вала пересекают ось вращения, их моменты относительно неё равны нулю.
3) Дифференциальные уравнения вращения твёрдого тела относительно неподвижной оси имеет вид:
,
где Мс
момент сил сопротивления, равный Мс=kω2,
тогда:
.
Получили дифференциальные уравнения первого порядка относительно неизвестной функции ω(t).
Разделяя переменные,
получим:
.
Вычисляем неопределённые интегралы отдельно левой и правой частей:
.
Произвольную
постоянную определяем из начальных
условий: t0=0,
ω(t0)=ω0:
.
Подставляя значение С1, получим закон изменения угловой скорости:
.
Если угловая скорость уменьшится в два раза, то это произойдёт в момент времени:
.
Пример 2
|
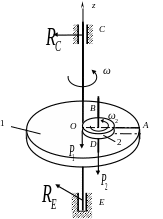
По радиусу ОА однородного горизонтального диска 1 сделан узкий сквозной паз, вдоль которого может перемещаться вертикальный стержень BD, жестко скрепленный с однородным диском 2, вращающимся с постоянной угловой скоростью ω2. Радиусы дисков равны R и r, а веса P1 и P2 соответственно. Диск 1 вращался вокруг вертикальной оси Oz, перпендикулярной к его плоскости, с постоянной угловой скоростью ω0. При этом обод диска 2 касался оси Oz. Определить угловую скорость диска 1 в момент, когда центр диска 2 находится на ободе диска 1. |
Решение.
1) Определяем состав исследуемой механической системы.
Механическая система состоит из двух твёрдых тел: диска 1 и диска 2.
2) Проводим кинематический анализ движений тел и материальных точек, входящих в исследуемую систему:
– диск1 совершает вращательное движение вокруг неподвижной оси Oz;
– диск 2 совершает сложное движение, состоящее их двух движений: переносного вращательного вокруг оси Oz с угловой скоростью ω и относительного вращательного вокруг оси BD с постоянной угловой скоростью ω2.
3) Описываем и обозначаем все внешние силы, действующие на тела и материальные точки, входящие в рассматриваемую систему:
Силы
тяжести дисков
и
приложенные в их центрах тяжести и
направленные параллельно оси Oz.
Реакция подпятника
,
приложенная в точке Е
и направленная в произвольном направлении
в пространстве. Реакция подшипника
,
направленная перпендикулярна оси Oz.
4) Записываем теорему об изменении момента количества движения механической системы относительно оси Oz:
(1)
где Lz –
момент количества движения механической
системы;
‑
сумма моментов всех внешних сил,
действующих на тела, входящие в
механическую систему, относительно той
же оси.
Определяем моменты
внешних сил:
,
,
так как эти силы параллельны оси Oz;
,
,
так как эти силы пересекают ось
Oz.
Тогда из уравнения (1) следует, что Lz(t)=const, т.е. момент количества движения механической системы в момент времени t0=0 и в момент времени tк равны: Lz(t0)= Lz(tк).
Механическая система состоит из двух твердых тел, поэтому
Lz(t)= Lz1(t)+ Lz2(t) ,
где Lz1(t), Lz2(t) – моменты количеств движения дисков 1 и 2.
Диск 1 совершает
вращательное движение вокруг неподвижной
оси
и
его момент количества движения равен:
Lz1(t0)=I1ω0,
Lz1(tк)=I1ω,
где I1 –
момент инерции диска 1 относительно оси
Oz.
Для однородного
диска
.
Диск 2 участвует в двух движениях и момент количества абсолютного движения относительно неподвижной оси равен сумме момента относительно той же оси количества движения его центра масс, в предположении, что в нём сосредоточена вся его масса, и момента относительно оси, проходящей через его центр масс количеств относительного движения диска по отношению к поступательно перемещающимся координатным осям:
,
,
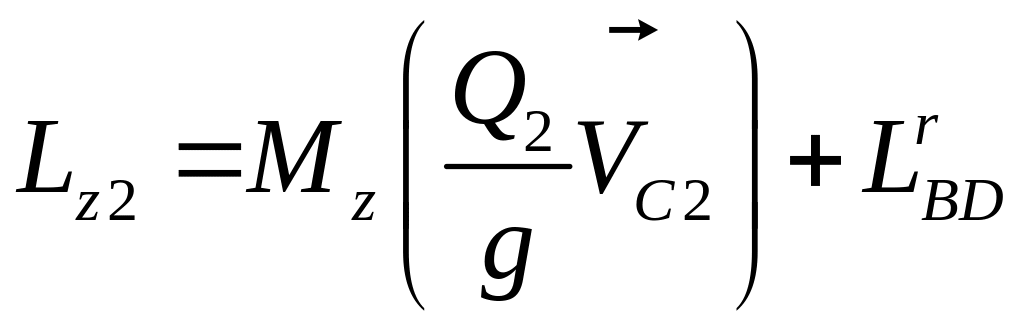(5)
где
‑
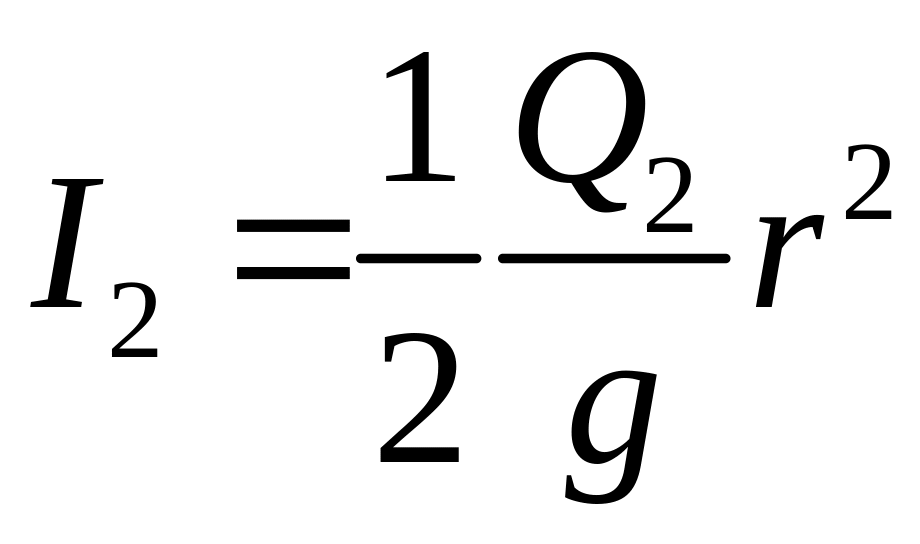момент инерции диска 2 относительно
собственной оси.
,
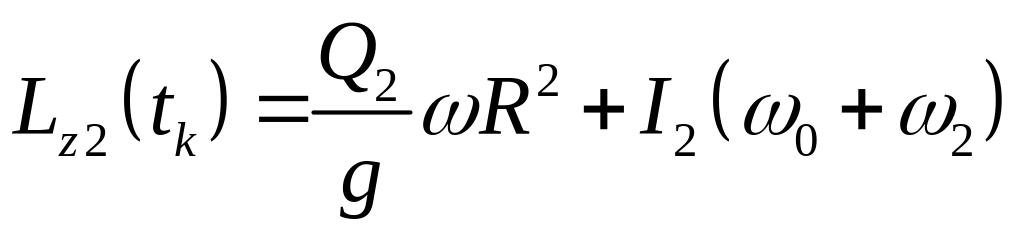(6)
Подставляя в (2) выражения (4-6) с учётом (3), получаем:
, откуда
