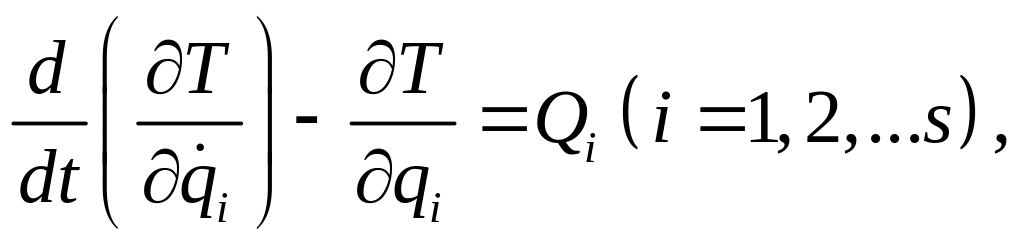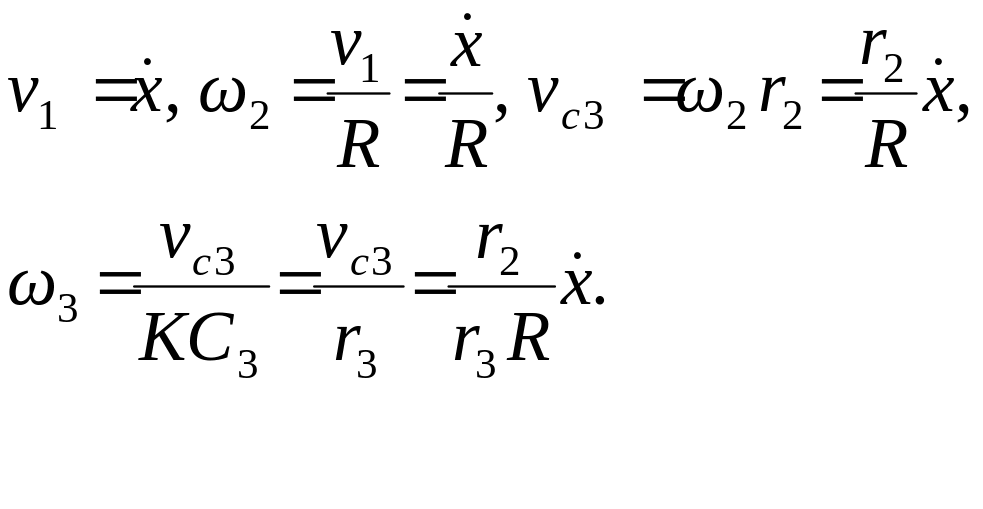4. Дифференциальные уравнения Лагранжа второго рода

Уравнения Лагранжа для обобщенных координат являются обыкновенными дифференциальными уравнениями второго порядка. Их число совпадает с числом обобщенных координат (числом степеней свободы).

Данное уравнение имеет следующую структуру

(4.1)

где - обобщенные координаты и обобщенные скорости точек системы, Т – кинетическая энергия системы, Q_i – обобщенная сила системы, соответствующая выбранной обобщенной координате, S – число степеней свободы системы.

Обобщенная сила Q_i - вычисляется по формуле

(4.2)

где n – число материальных точек, s – число степеней свободы, - равнодействующая активных сил и реакций неидеальных связей, приложенных к точке системы.

Для исследования динамики движения механической системы с одной степенью свободы рекомендуется следующая последовательность действий:

1) Выбрать систему координат и ввести независимую обобщенную координату;

2) Определить обобщенную силу системы, соответствующую избранной обобщенной координате. Для этого необходимо:

- изобразить все активные силы системы и реакции неидеальных связей (силы трения);

- дать независимое обобщенное возможное перемещение системе, соответствующее выбранной обобщеной координате;

- вычислить сумму работ всех активных сил, включая реакции неидеальных связей, на обобщенном возможном перемещении и определить обобщенную силу как коэффициент при обоющенном возможном перемещении;

3) Вычислить кинетическую энергию системы материальных точек;

4) Найти частные производные кинетической энергии по обобщенной скорости и координате и производную по времени;

5) Полученные в п.3, 4 результаты подставить в уравнение Лагранжа;

6) Определить искомую величину или провести интегрирование дифференциального уравнения движения.

4.1. Пример решения задачи

В предлагаемой задаче система имеет одну степень свободы, следовательно, ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение.

За обобщенную координату q рекомендуется принять: в задачах, где требуется определить линейное ускорение тела - перемещение x соответствующего груза или центра масс катка; в задачах, где требуется определить угловое ускорение ε угол поворота φ соответствующего шкива или катка.

Для составления уравнения сначала следует вычислить кинематическую энергию T системы и выразить все вошедшие в нее скорости через обобщенную скорость, т.е. через , если обобщенная координата х , или через , если обобщенная координата φ. Затем вычислить обобщенную силу Q. Для этого сообщать системе возможное (бесконечно малое) перемещение, при котором выбранная координата, т.е. х (или φ), получает положительное перемещение δх (или δφ), и вычислить сумму элементарных работ всех сил на этом перемещении; в полученном выражении необходимо все другие элементарные перемещения выразить через δх (или через δφ, если обобщенная координата φ), и вынести δх (или δφ) за скобки. Коэффициент при δх (или δφ) и будет обобщенной силой Q.

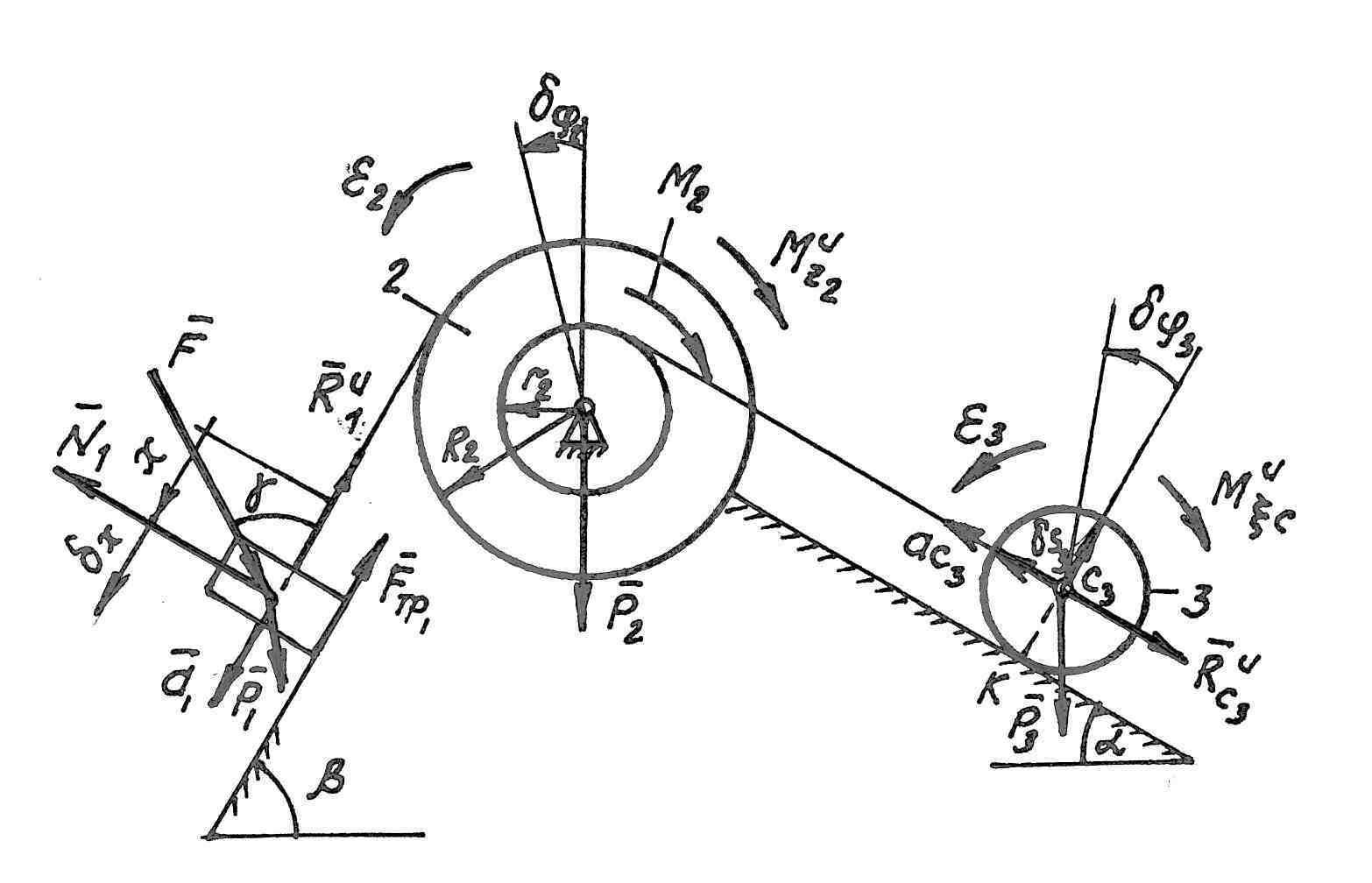
Механическая система состоит из ступенчатого шкива 2 (радиусы ступеней R₂ и r₂), груза 1 и сплошного катка 3, прикрепленных к концам нитей, намотанных на ступени шкива. На шкив при его вращении действует момент сил сопротивления M₂ Радиус инерции ступенчатого шкива 2 ρ_z2, f – коэффициент трения скольжения груза 1 о наклонную плоскость.

Дано: R₂ = R, r₂ = 0,6 R, Р₁ = 6Р, Р₃ = 3Р, М₂ = 0,2 РR, F = 2P, P_z2 = 0,5R, f = 0,1, α = 30^˚, β = 60˚, γ = 60˚.

Определить: а₁ – ускорение груза 1.

1.Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение х груза 1 (q = х), полагая, что груз движется вниз, и отсчитывая х в сторону движения; составим уравнение Лагранжа

.

(4.3)

2. Определим кинетическую энергию T системы, равную сумме энергий всех тел:

.

(4.4)

Так как груз 1 движется поступательно, шкив 2 вращается вокруг неподвижной оси, а каток 3 движется плоскопараллельно, то

(4.5)

где моменты инерции шкива 2, поскольку известен его радиус инерции, а каток 3 – сплошной (его радиус обозначим r₃) определяются по формулам:

(4.6)

3. Все скорости, входящие в , выразим через обобщенную скорость , равную, очевидно, v_1. Если при этом учесть, что , а , и что точка является для катка 3 мгновенныи центром скоростей, то получим:

(4.7)

Подставив величины (4.7) и (4.6) в равенства (4.5), а затем значения в равенство (4.4), найдем окончательно, что

(4.8)

Так как здесь зависит только от , то

(4.9)

4. Найдем обобщенную силу . Для этого изобразим силы, совершающие при движении системы работу, т.е. силы и момент сил сопротивления , направленный против вращения шкива. Затем сообщим системе возможное (элементарное) перемещение, при котором обобщенная координата получает положительное приращение , и покажем перемещение каждого из тел; для груза 1 это будет для шкива 2 – поворот на угол , для катка 3 – перемещение его центра. После этого вычислим сумму элементарных работ сил и момента на данных перемещениях. Получим

(4.10)

Все входящие сюда перемещения надо выразить через . Учтя, что зависимости между элементарными перемещениями здесь аналогичны зависимостям (3.23) между соответствующими скоростями, получим

(4.11)

Сила трения скольжения

Силу нормальной реакции найдем из условия равенства нулю проекций на ось, перпендикулярную направлению движения груза 1 всех сил, действующих на него.

(4.12)

Подставляя эти значения в равенство (4.10) и вынося за скобки, найдем, что

(4.13)

Коэффициент при в полученном выражении и будет обобщенной силой, следовательно,

или

(4.15)

Подставляя полученные величины (4.9) и (4.15) в уравнение (4.3), получим:

Ответ: