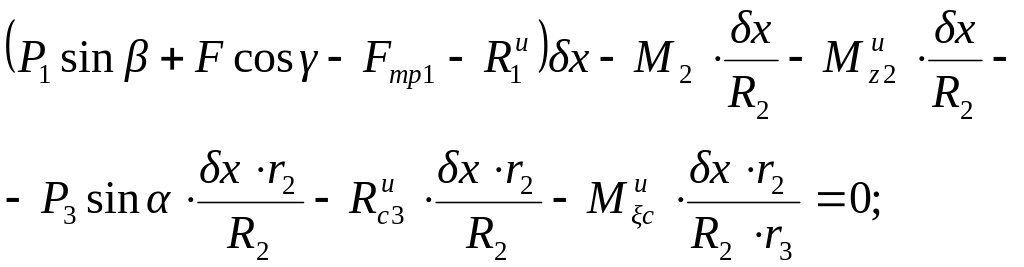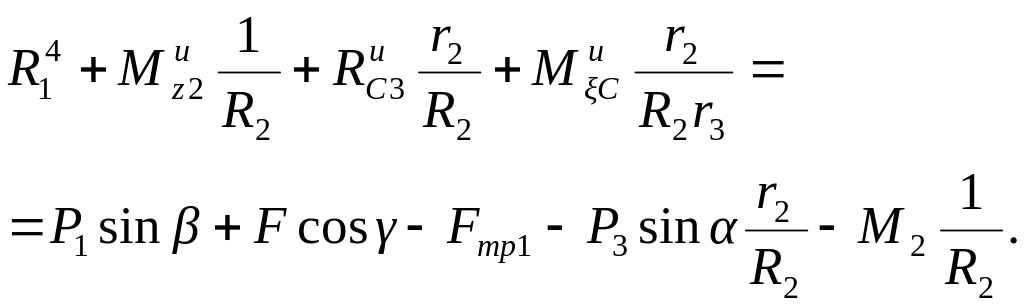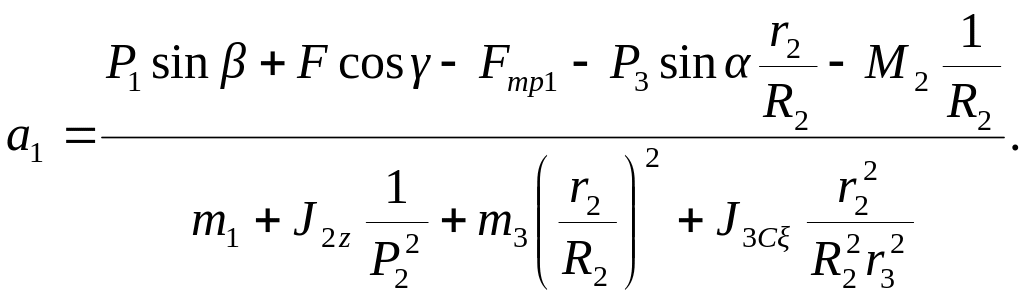3. Общее уравнение динамики движения механической системы

При движении материальной системы, подчиненной идеальным удерживающим связям, сумма работ активных сил и сил инерции на любых возможных перемещениях точек системы равна нулю:

	(3.1)
если	(3.2)

то общее уравнение динамики имеет вид:

(3.3)

Преимущество общего уравнения динамики по сравнению с другими теоремами динамики заключается в том, что в его формулировке отсутствуют реакции идеальных связей. Если не все связи являются идеальными, например, имеются связи с трением, то, применяя общее уравнение динамики, следует к активным силам добавлять реакции, соответствующие неидеальным связям.

Вычисление суммы работ сил инерции на возможных перемещениях точек твердого тела производится по формулам:

а) При поступательном движении:

(3.4)

где - равнодействующая сил инерции ( ); - ускорение любой точки твердого тела; - возможное перемещение любой точки твердого тела.

б) При вращении вокруг неподвижной оси:

(3.5)

где - главный момент сил инерции относительно оси вращения ; - момент инерции твердого тела относительно оси вращения; - угловое ускорение вращательного движения твердого тела; - возможное угловое перемещение твердого тела.

в) При плоском движении:

(3.6)

где - главный вектор сил инерции ; - ускорение центра масс твердого тела;

- главный момент сил инерции относительно оси, проходящей через центр масс С твердого тела перпендикулярно плоскости движения ; - момент инерции твердого тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения; - угловое ускорение твердого тела; - возможное перемещение центра масс С твердого тела; - возможное угловое перемещение твердого тела.

При решении задач с помощью общего уравнения динамики рекомендуется следующая последовательность действий:

1) Изобразить на рисунке активные и реакции, соответствующие неидеальным связям (силы трения);

2) Определить главные векторы и главные моменты сил инерции масс системы;

3) Дать возможное перемещение одной из точек системы и выразить возможные перемещения точек приложения всех сил, указанных в 1, 2, через это возможное перемещение.

4) Вычислить сумму работ всех сил на возможных перемещениях точек системы; составить общее уравнение динамики, приравняв в вычисленную сумму работ сил нулю;

5) Определить искомую величину либо провести интегрирование дифференциального уравнения движения.

3.1. Пример решения задачи.

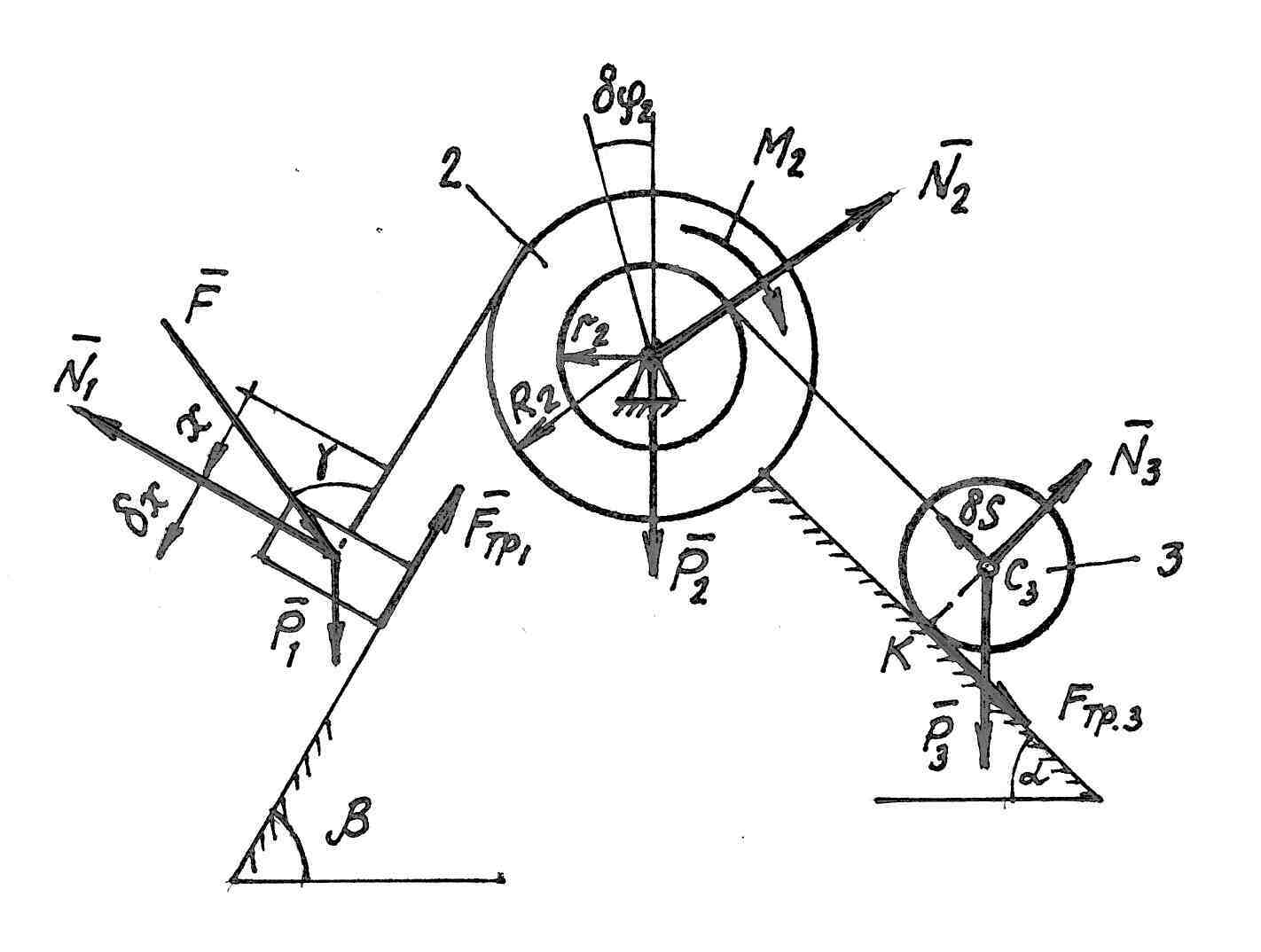
Рис.2.1.

Механическая система состоит из ступенчатого шкива 2 (радиусы ступеней R₂ и r₂), груза 1 и сплошного катка 3, прикрепленных к концам нитей, намотанных на ступени шкива. На шкив при его вращении действует момент сил сопротивления M₂ Радиус инерции ступенчатого шкива 2 ρ_z2, f – коэффициент трения скольжения груза 1 о наклонную плоскость.

Дано: R₂ = R, r₂ = 0,6 R, Р₁ = 6Р, Р₃ = 3Р, М₂ = 0,2 РR, F = 2P, P_z2 = 0,5R, f = 0,1, α = 30^˚, β = 60˚, γ = 60˚.

Определить: а₁ – ускорение груза 1.

1. Материальная система состоит из трех твердых тел и имеет одну степень свободы. Будем считать, что ускорение груза 1 направлено вниз по наклонной плоскости .

2. Определим вид движений тел, входящих в систему. Груз 1 совершает поступательное движение; шкив 2 совершает вращательное движение вокруг неподвижной оси; каток 3 – совершает плоское движение.

3. Изобразим на рисунке активные силы и реакции, соответствующие неидеальным связям .

4. Определим главные вектора и главные моменты сил инерции масс системы и изобразим их на рисунке.

	(3.7)
	(3.8)

5. Дадим возможное перемещение центру масс груза 1 - и выразим возможные перемещения точек приложения всех сил, указанных в пунктах 3 и 4, через это возможное перемещение.

.

(3.9)

6. Вычислим сумму работ всех сил, указанных в пунктах 3 и 4, на возможных перемещениях точек системы и составим общее уравнение динамики, приравняв вычисленную сумму работ сил нулю.

	(3.10)
	(3.11)

После сокращения на заданное возможное перемещение получаем:

(3.12)

Так как

	(3.13)
то	(3.14)

Сила трения скольжения

Силу нормальной реакции найдем из условия равенства нулю проекций на ось, перпендикулярную направлению движения груза 1 всех сил, действующих на него

(3.15)

Момент инерции шкива 2, поскольку известен его радиус инерции, а каток 3 – сплошной

(3.16)

Окончательно ускорение груза 1 равно