2.1. Пример решения задачи.

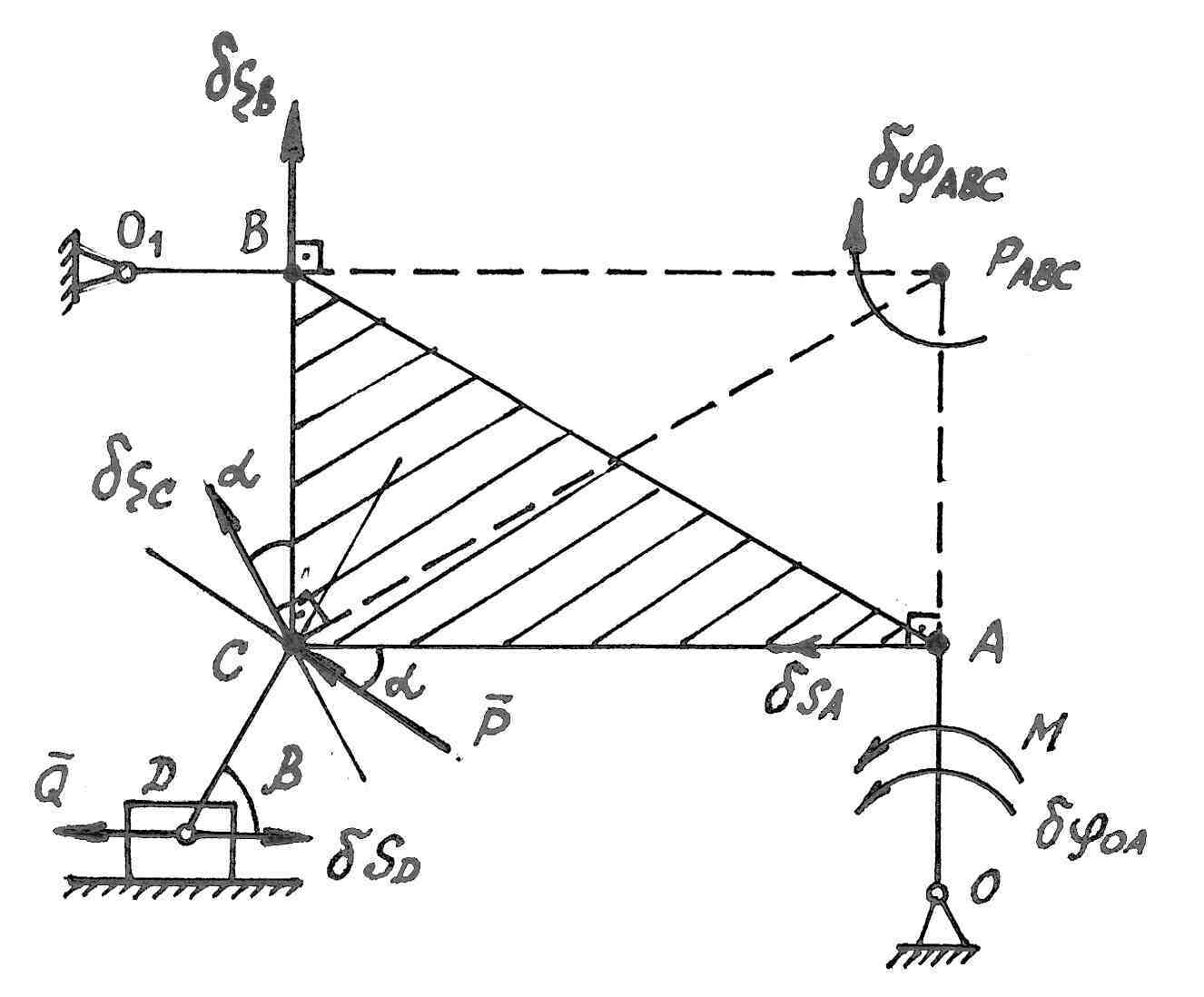
Плоский механизм с идеальными связями находится в равновесии под действием сил , и пары сил с моментом , приложенной к звену ОА. Используя принцип возможных перемещений, определить величину момента при следующих исходных данных: Звено АВС – прямоугольный треугольник с углом при вращении А, равным .

Для решения задачи воспользуемся ПВП, согласно которому

(2.3)

где - элементарные работы активных сил на соответствующих возможных перемещениях.

Рассматриваемый механизм имеет одну степень свободы. Его элементы (звенья) совершают следующие виды движений: кривошип ОА и О₁В – вращательное движение относительно осей, проходящих через точки О и О₁, треугольник АВС и шатун D – поступательное.

Чтобы составить уравнение (2.3), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: - угловое перемещение звена ОА, и - линейные перемещения точек C и D.

Примем за независимое возможное перемещение и установим кинематические зависимости между указанными возможными перемещениями. Способ их нахождения аналогичен определению скоростей точек при плоском движении.

Сначала найдем возможное перемещение общей для звеньев ОА и АВС точки А. При вращательном движении звена ОА относительно точки О имеем

(2.4)

Направление определяются направлением .

Для определения возможного перемещения точки С находим мгновенный центр вращения звена АВС, зная линии действия перемещений двух точек А и В этого звена - и . Проводя перпендикуляры к направлениям и , получим точку их перемещения - . При плоско-параллельном движении все точки звена АВС совершают вращательное движение относительно этой точки.

Тогда линейные возможные перемещения точек А, В и С будут пропорциональны их расстояниям до мгновенного центра вращения:

(2.5)

Находим угловое перемещение звена АВС:

(2.6)

его направление определяется направлением (рис. ).

Далее находим и изображаем линейное перемещение точки С

(2.7)

где .

Направление определяется направлением (вращение вокруг точки происходит против хода часовой стрелки).

В случае необходимости находим по направлению : .

Зная и линию действия возможного перемещения точки D – горизонталь находим , используя следствие из теоремы о проекциях скоростей двух точек плоской фигуры на ось, проходящую через эти точки.

Запишем

	(2.8)

Направление находится из условия равенства проекции возможных перемещений и на ось проходящую через данные точки (см.рис. )

Теперь запишем уравнение (1) для механизма:

(2.9)

Заменяя и их значениями (2.7) и (2.8) и вынося одновременно за скобки, получим:

(2.10)

Так как :

откуда

После подстановки исходных данных находим