Динамика материальной точки

1. Основные понятия и определения

Основное уравнение динамики:

, (1)

где - равнодействующая системы сил.

Дифференциальные уравнения движения материальной точки в координатной форме:

; ; .

Две основные задачи динамики точки:

Первая (прямая) задача: Зная массу точки и законы ее движения, найти действующую на точку силу. Для решения этой задачи дважды дифференцируем законы движения по времени (определяем , , ); подставляем в дифференциальное уравнение; находим проекции силы :

, , .

Тогда модуль силы:

;

направляющие косинусы:

; ; .

Вторая (обратная) задача: По заданной массе точки и действующей на точку силе определить движение этой точки. Для решения этой задачи необходимо в левую часть уравнений подставить массу m, а в правую часть проекции действующей силы. Полученные дифференциальные уравнения дважды проинтегрировать по времени с учетом начальных условий.

2. Примеры решения задач

2.1 Частица массой m, несущая заряд электричества e, находится в однородном электрическом поле с переменным напряжением (A и k — заданные постоянные). Определить движение частицы, если известно, что в электрическом поле на частицу действует сила , направленная в сторону напряжения . Влиянием силы тяжести пренебречь. Начальное положение частицы принять за начало координат; начальная скорость частицы равна нулю.

Решение

1. Расчетная схема.

И з условий задачи понятно, что точка М (тело) будет двигаться вдоль оси у (точка M₀ совпадает с О; V₀=0).

2. На точку М действует сила ( , ).

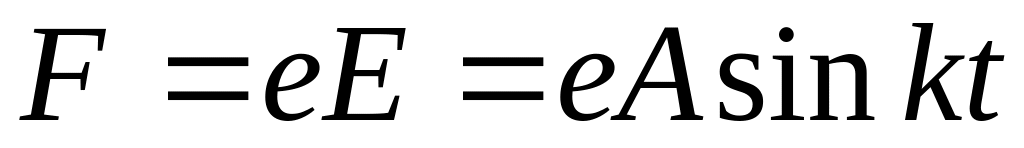3. Составим дифференциальное уравнение движения точки М в проекции на ось у:

;

4. Разделим переменные и проинтегрируем:

; ; .

Перепишем уравнение, разделим переменные и проинтегрируем ещё раз:

;

, откуда

.

2.2 Тело весом Р, находящееся на гладкой горизонтальной плоскости, притягивается к центру О на этой плоскости силой, обратно пропорциональной квадрату расстояния тела от точки О. В начальный момент тело находилось от притягивающего центра на расстоянии b и имело скорость, равную нулю. Сила притяжения тела в этот момент была равна . Определить скорость тела, после того как оно пройдёт половину первоначального расстояния до точки О.

Решение

1. Расчетная схема

2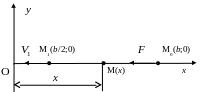 . На точку М действуют силы: (P=mg); (N — нормальная реакция плоскости, N=P); ( где K₁ — коэффициент пропорциональности. По условию в точке М₀ выполнялось равенство , отсюда найдём K₁=kP, т.е. )

Силы и перпендикулярны плоскости Оxy и на расчетной схеме не изображены.

1. Составим дифференциальное уравнение движения точки М в проекции на ось х:

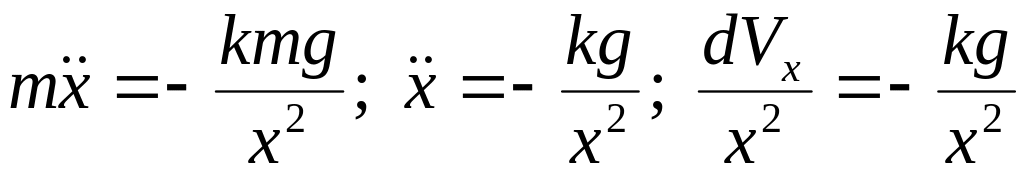
2. В дифференциальном уравнении три переменных: 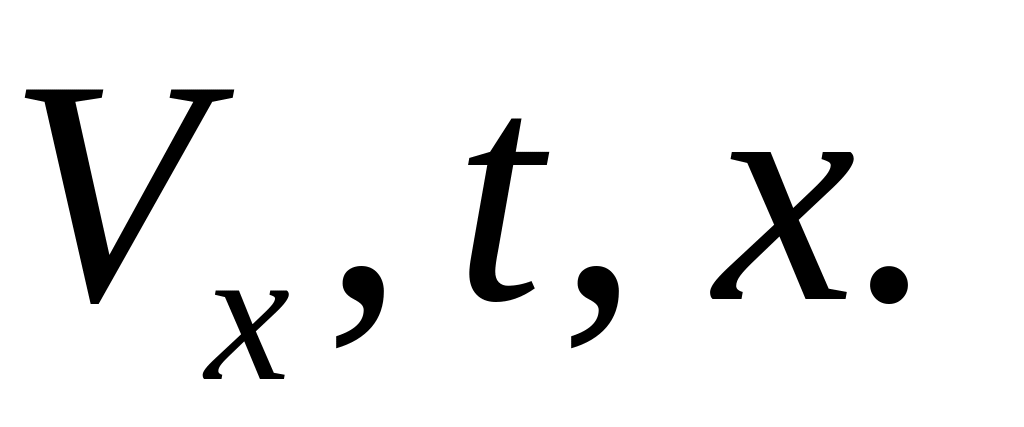Умножим обе части уравнения на 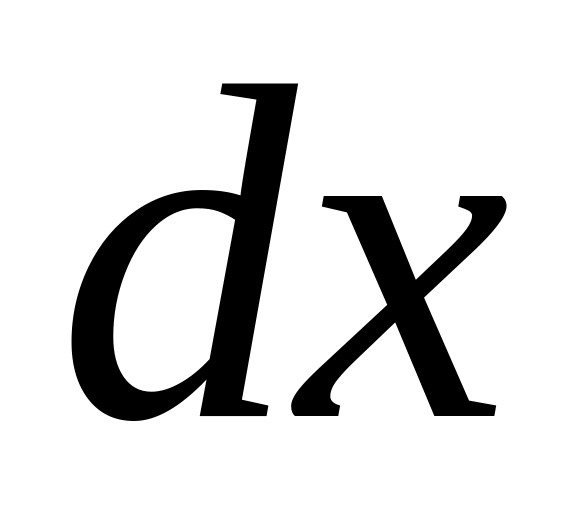и зная, что 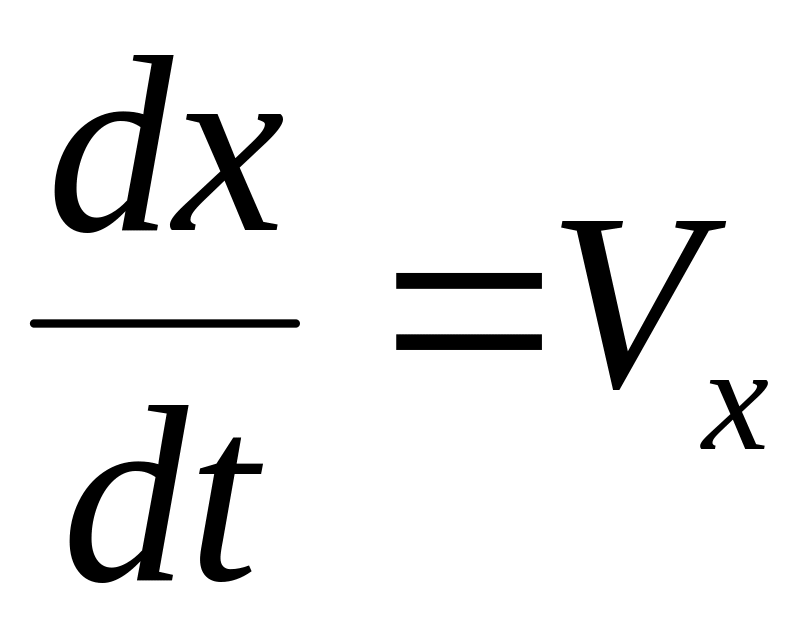, получим , проинтегрируем:

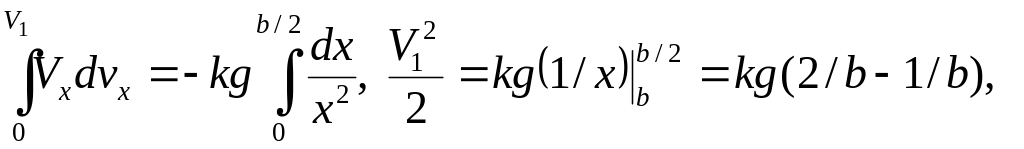отсюда

2.3 Корабль массой 10⁷ кг движется со скоростью 16 м/с. Сопротивление воды пропорционально квадрату скорости корабля и равно 3^.10⁵ Н при скорости 1 м/с. Какое расстояние пройдет корабль, прежде чем его скорость станет равной 4 м/с? За какое время корабль пройдет это расстояние?

Решение

Так как корабль (твердое тело) совершает поступательное движение и размеры корабля не существенны для условий данной задачи, то заменим корабль материальной точкой.

1. Изобразим материальную точку М в выбранной системе координат в текущий момент времени. Покажем также начальное М₀ и конечное М₁ положения материальной точки. Назовем это расчетной схемой.

Расчетная схема:

2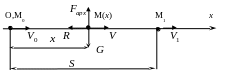 . На точку М действуют силы: —сила тяжести, (выталкивающая сила Архимеда), сила сопротивления Н, где μ — коэффициент сопротивления ([μ] =  ). Из условий задачи следует, что   . Покажем силы на расчетной схеме.

3. Составляем дифференциальное уравнение движения точки М в проекции на ось х:

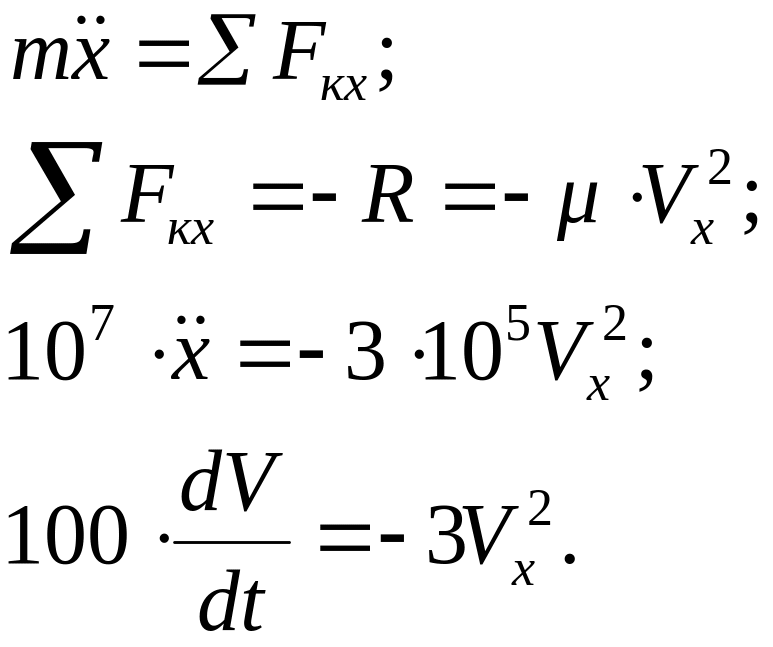
Так как движение прямолинейное, то

. (1)

4. Решим дифференциальное уравнение (1), для чего разделим переменные и проинтегрируем:

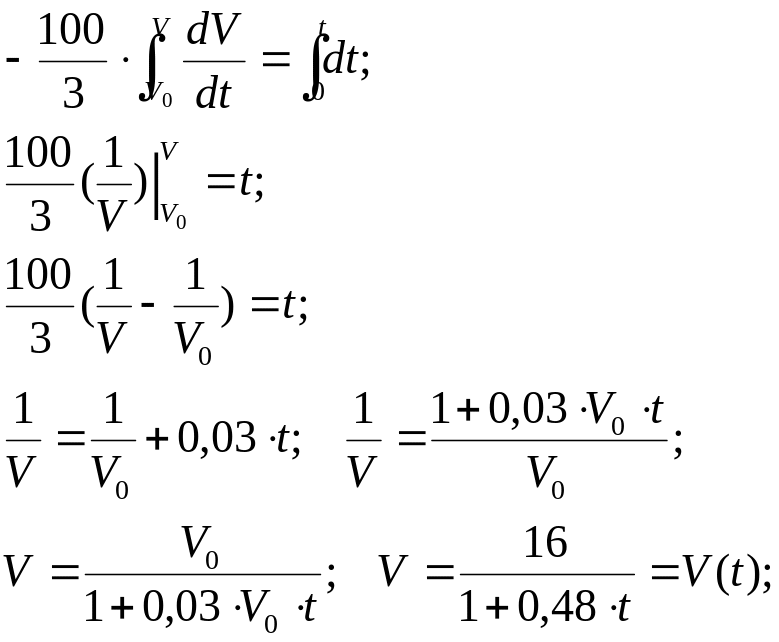
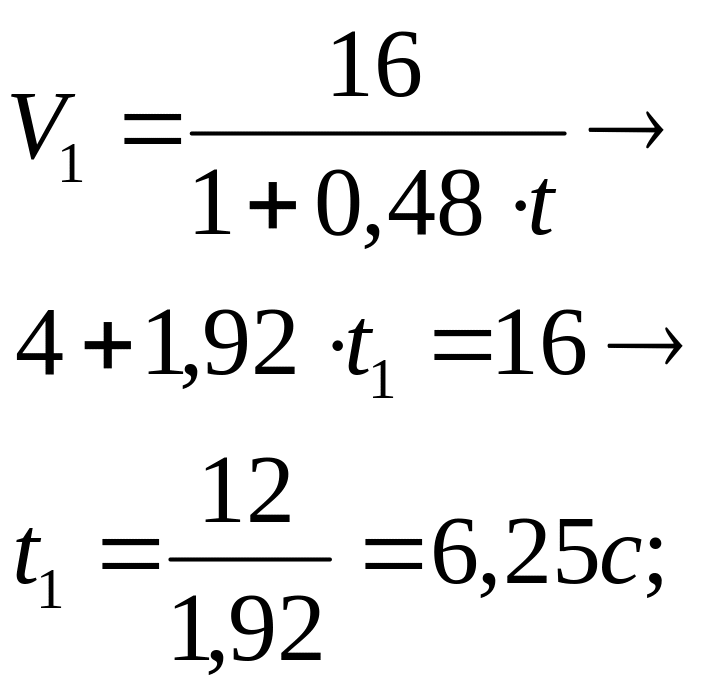(2)

При t=t₁, V=V₁: : , откуда

t₁=6,25 c.

Далее нужно найти S₁ и здесь есть два варианта:

а) уравнение (2) представить в виде

. (3)

разделить переменные и проинтегрировать в пределах от 0 до t₁ (t₁ известно), найти S₁;

б) чаще используется такой вариант для случая, когда R=R(V):

запишем дифференциальное уравнение (1), умножим обе части на dx:

100^.V^.dV = –3^.V²dx, разделим переменные и проинтегрируем

,

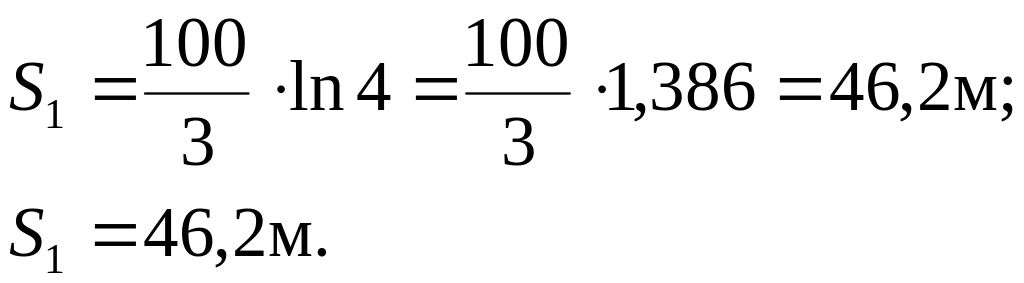
Вариант второй предпочтительнее, так как быстрее приводит к ответу.

2.4 Подводная лодка, не имевшая хода, получив небольшую отрицательную плавучесть P, погружается на глубину, двигаясь поступательно. Сопротивление воды при небольшой отрицательной плавучести можно принять пропорциональным первой степени скорости погружения и равным kSV, где k — коэффициент пропорциональности; S — площадь горизонтальной проекции лодки; V — величина скорости погружения. Масса лодки равна М. Определить скорость погружения V, если при t = 0 скорость V₀ = 0.

Решение