32.Фазовая плоскость. Обоснование одной (любой) из фазовых картин.
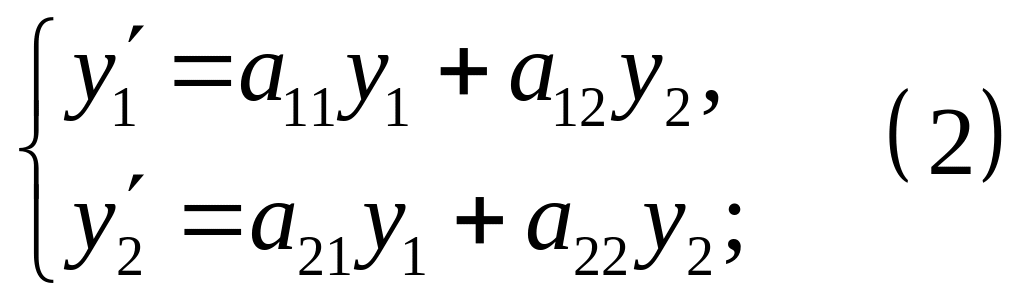
Графики решений (интегральные кривые) .
Определение:
Фазовая плоскость системы (1) – пространство
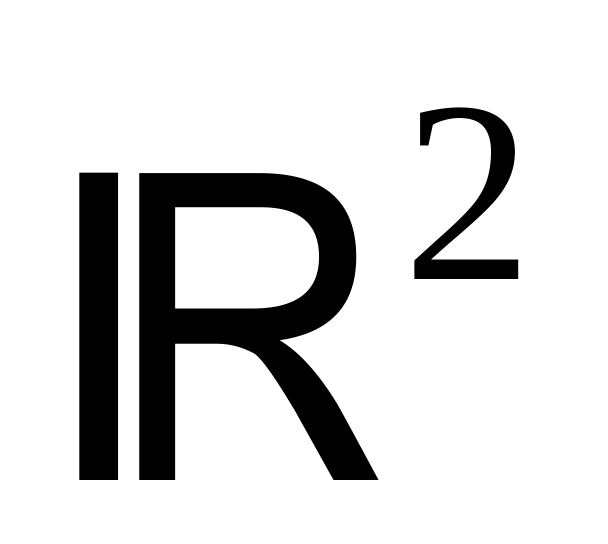переменных
Фазовая траектория системы (1) – проекция любой интегральной кривой этой системы на фазовую плоскость.
Фазовая картина системы (1) – совокупность всех её фазовых траекторий.
В зависимости от
свойств матрицы
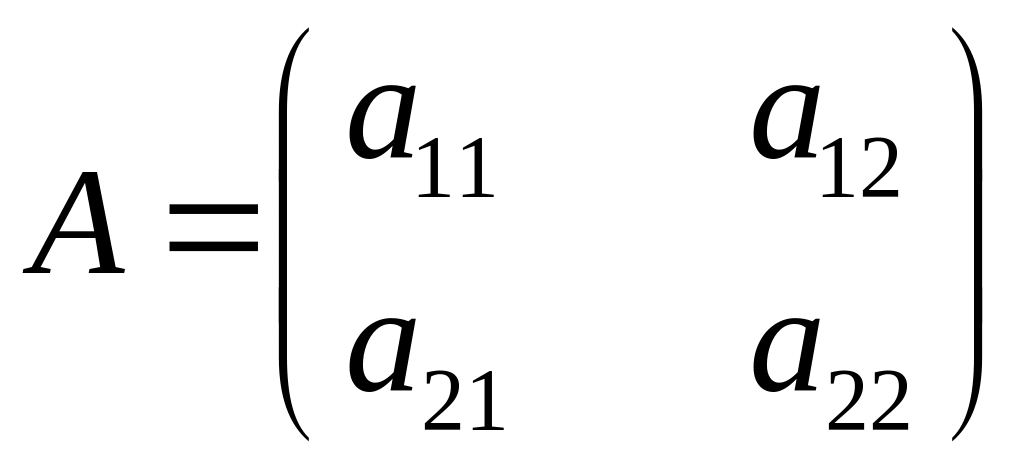системы (1) существуют 9 различных фазовых
картин. Они зависят от собственных
значений
матрицы
.
находятся как корни квадратного
уравнения. Будем считать, что корней
всегда 2, но, быть может, они совпадают.
Начало координат – всегда одна из
фазовых траекторий (соответствующих
нулевому решению):
.
и 2 линейно независимых собственных вектора |
Дикритический узел |
Фазовые траектории – всевозможные лучи, выходящие из начала координат. |
|
Обоснуем пункт 6 (дикритический узел):
,
2 линейно независимых собственных
вектора. Из линейной алгебры: только
для матрицы
вида
справедливы такие свойства. Значит,
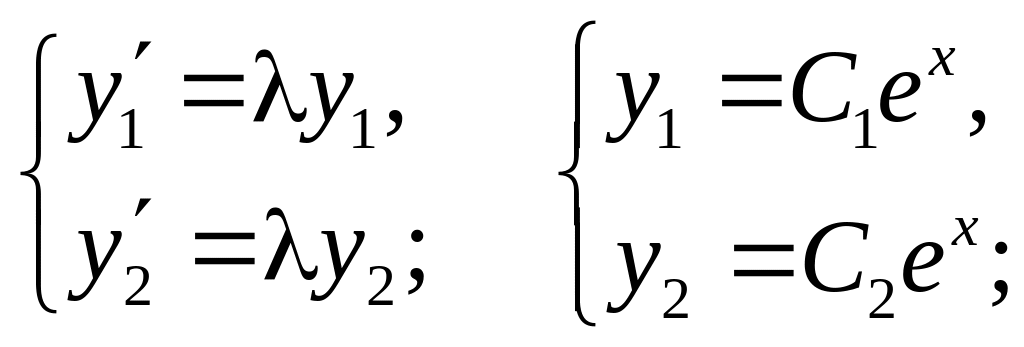
отвечает своя
фазовая траектория.
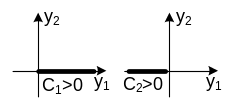
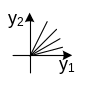Если
то
– начало координат (самостоятельная
фазовая траектория).
полуоси
– фазовые траектории.
фазовые траектории в I
четверти.
При
(оба
):
И т. д.
33.Линейные интегральные уравнения второго рода. Случай вырожденного ядра.
Определение:
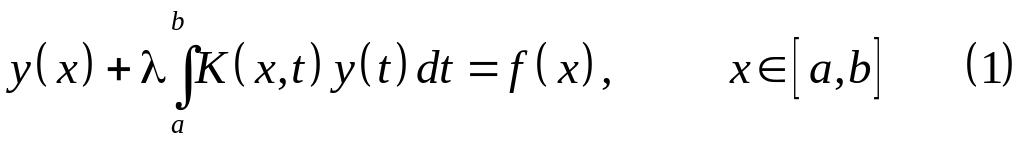
(1) – линейное
интегральное уравнение второго рода.
;
- линейный оператор.
Если , то (1) – однородное, иначе – неоднородное.
параметр. 
ядро.
Все функции в (1) – непрерывные (и тоже).
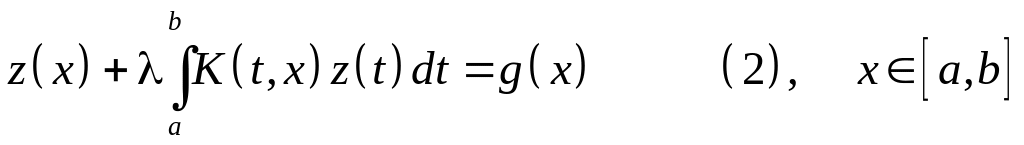
(2) – союзное уравнение к (для, по отношению) уравнению (1).
Далее всегда
условимся считать, что
.
Уравнения (1) и (2) не имеют общих формул для решения.
Теоремы Фредгольма.
Однородные уравнения (1) и (2) имеют конечное и притом одинаковое число линейно независимых решений.
(альтернатива Фредгольма). Справедливо одно и только одно из следующих утверждений:
а) неоднородное
уравнение (1) имеет единственное решение
для
.
б) соответствующее однородное уравнение (1) имеет ненулевые решения.
Для того, чтобы неоднородное уравнение (1) было разрешимым, необходимо и достаточно, чтобы
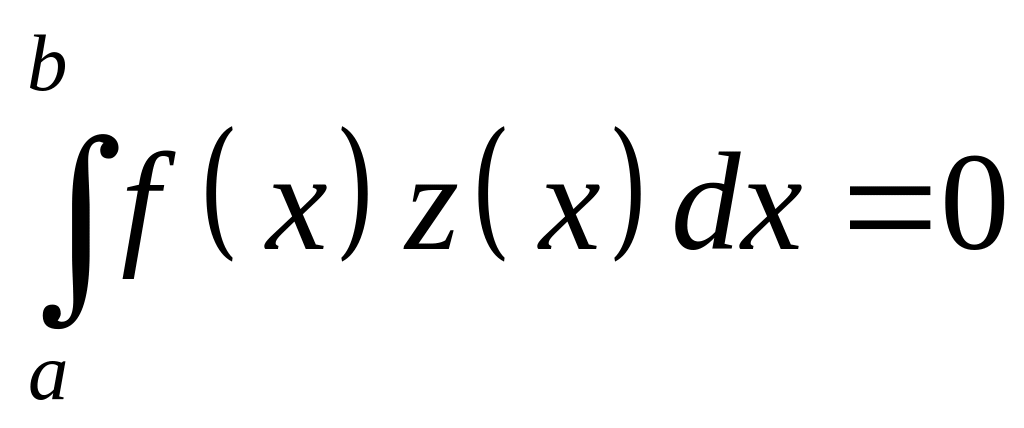для любого решения
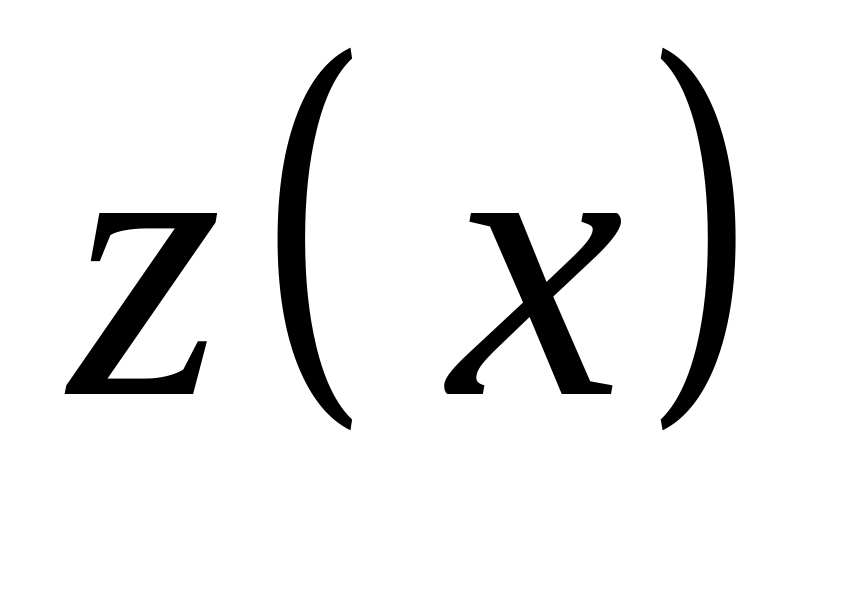соответствующего однородного уравнения.
Определение:
Ядро уравнения
(1) – вырожденное, если
.
,
,
(
–
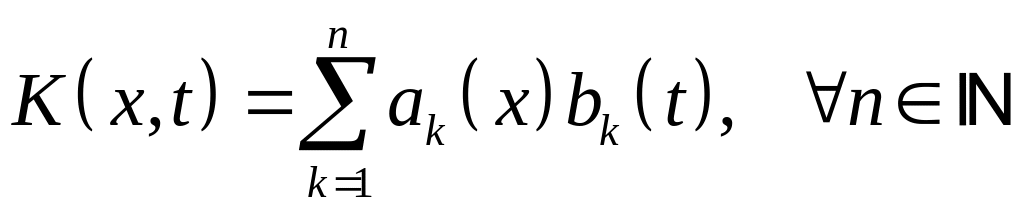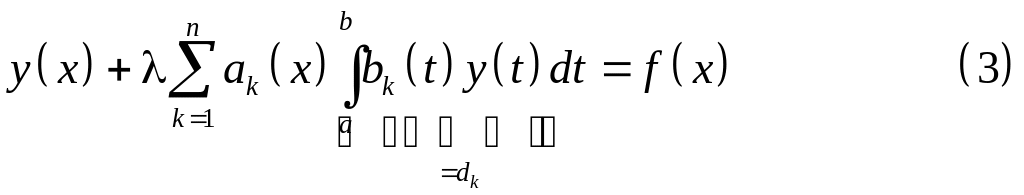константы)
, 
;
Найдем :
Возьмем
,
домножим обе части уравнения (4) на
;
проинтегрируем от
до
.
.
, 
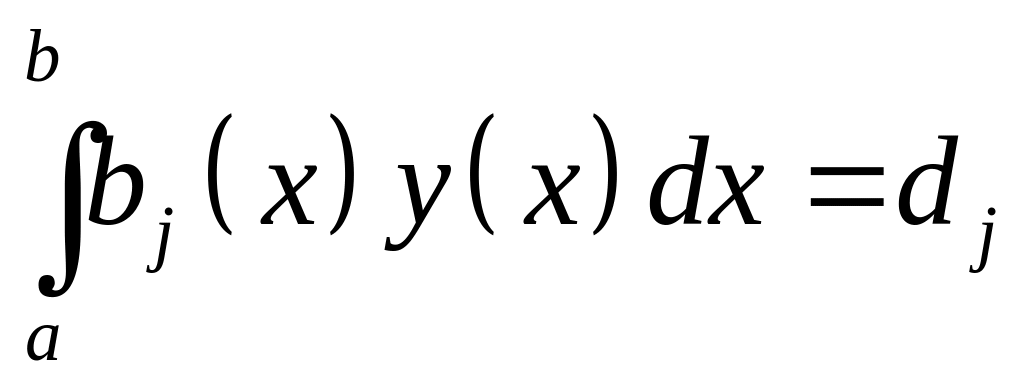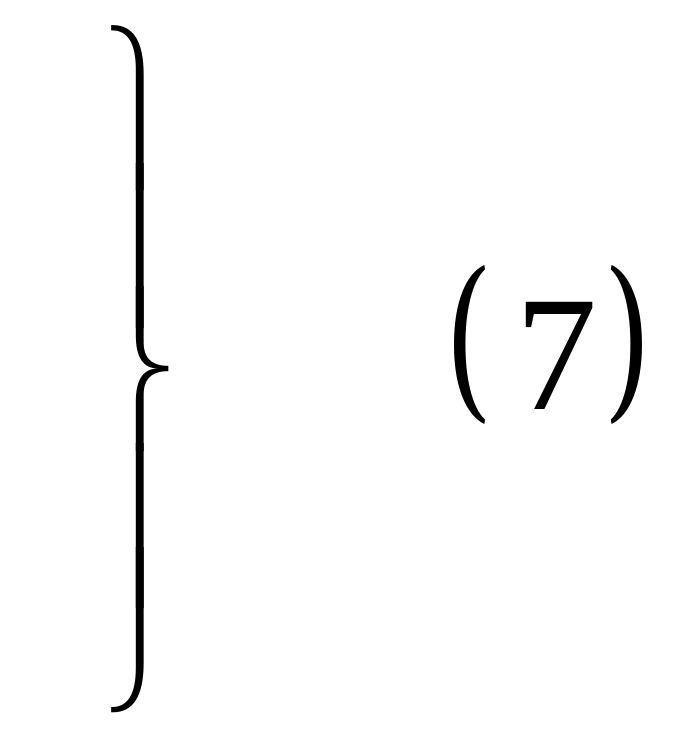
(8) – система
линейных алгебраических уравнений.
Решив ее, найдем
.
План решения: 1.
найти
по формуле (7).
2. составить и решить систему (8). Если (8) не имеет решения, то (1) тоже. Иначе:
3. решение записывается по формуле (5).