
- •1. Основные понятия и факты связанные с д.У.
- •2.Существование, единственность и приближенное решение задачи Коши
- •3. Д.У., описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и д.Р.)
- •4. Приближенное построение интегральных кривых с помощью изоклин.
- •5. Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6. Линейные уравнения 1-ого порядка.
- •7. Уравнение Бернулли и Риккати.
- •8. Уравнения в полных дифференциалах.
- •9. Интегрирующий множитель
- •12. Уравнение Клеро и Лагранжа.
- •13. Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14. Системы д.У. Метод исключения. Общий интеграл.
- •15. Линейные однородные уравнения в частных производных. Задача Коши.
- •16. Квазилинейные уравнения в частных производных. Задача Коши.
- •17. Линейная зависимость функций и вронскиан.
- •18. Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •22.Метод Лагранжа для линейных уравнений.
- •23.Метод неопределенных коэффициентов для линейных уравнений.
- •24.Уравнения Эйлера.
- •25.Линейные однородные системы.
- •26.Линейные однородные системы с постоянными коэффициентами.
- •27. Метод Лагранжа для линейных систем.
- •29.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •31.Устойчивость решений. Система первого приближения. Критерий Рауса-Гурвица.
- •32.Фазовая плоскость. Обоснование одной (любой) из фазовых картин.
- •33.Линейные интегральные уравнения второго рода. Случай вырожденного ядра.
- •34.Задачи вариационного исчисления и понятие о способах их решения.
- •1. Основные понятия и факты связанные с д.У(1)
- •2.Существование, единственность и приближенное решение задачи Коши(2)
18. Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
![]()
![]() коэффициенты
уравнения;
коэффициенты
уравнения;
![]() непрерывны.
непрерывны.
Краткая запись
(1):
![]() .
.
![]() линейный оператор.
линейный оператор.
![]() .
.
Т.к. справа ноль, то уравнение однородное.
Свойства: 1.
![]() решение (1)
решение (1)
Линейная комбинация с любыми коэффициентами любых решений (1) – решение (1).
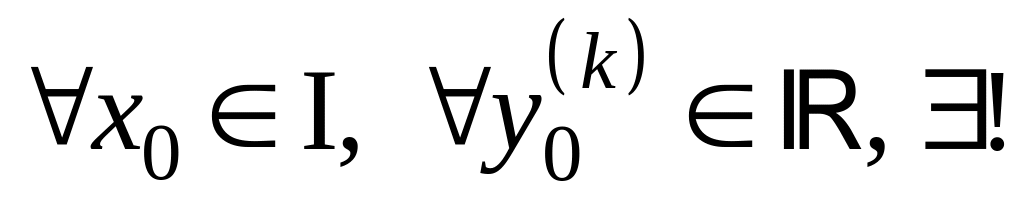 решение
уравнения (1),
решение
уравнения (1),
 такое,
что
такое,
что
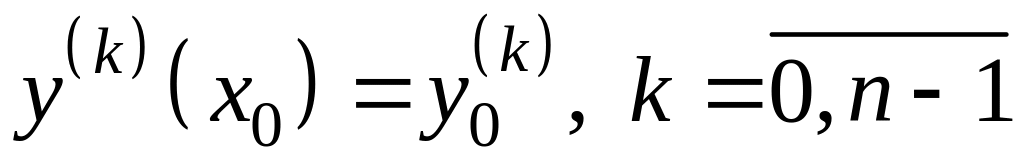 .
.
Теорема
1: Пусть
![]() решения
уравнения (1);
решения
уравнения (1);
![]() Тогда
линейно зависимы.
Тогда
линейно зависимы.
Доказательство:
Определитель этой системы –
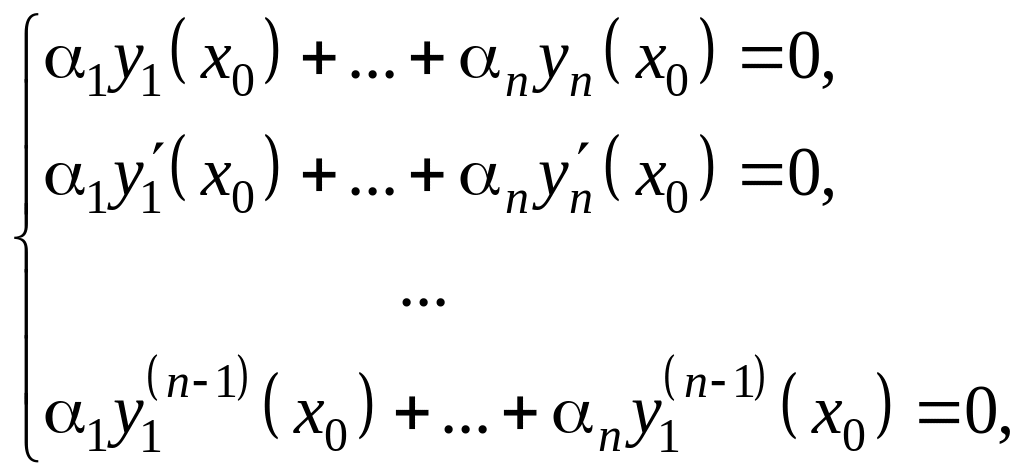
![]()
Тогда существует
нетривиальное решение. Выберем конкретное
нетривиальное решение системы
![]() .
По свойству 2
.
По свойству 2
![]() тоже
решение. Выберем
тоже
решение. Выберем
![]() .
.
![]() Наше решение в точке
удовлетворяет начальным условиям. С
другой стороны,
Наше решение в точке
удовлетворяет начальным условиям. С
другой стороны,
![]() тоже удовлетворяет условию
тоже удовлетворяет условию
![]() .
По свойству 3
.
По свойству 3
![]() .
Т. к. не все
.
Т. к. не все
![]() ,
то
линейно зависимы, ЧТД.
,
то
линейно зависимы, ЧТД.
Теорема 2. Пусть – решение (1). Тогда справедливо ровно 1 из следующих утверждений:
1.
![]()
2.
![]()
Доказательство:
Обоснуем, что не может где-то
![]() ,
а где-то не равняться.
,
а где-то не равняться.
Пусть
![]() .
Тогда
линейно зависимы, т. е.
.
Тогда
линейно зависимы, т. е.
![]()
![]() линейно независимы.
линейно независимы.
От противного.
Если бы были линейно зависимы, то по
теореме из предыдущего вопроса
![]() .
.
![]()
Если бы
![]() то
линейно зависимы.
то
линейно зависимы.
![]() линейно зависимы.
От противного.
От противного.
линейно зависимы.
От противного.
От противного.
19.Существование фундаментальной системы решений.
Определение: Фундаментальной системой решений (1) называется совокупность его линейно независимых решений.
Теорема 3. Для уравнения (1) существует фундаментальная система решений.
Доказательство:
Возьмем числа
![]() .
Потребуем, чтобы
.
Потребуем, чтобы
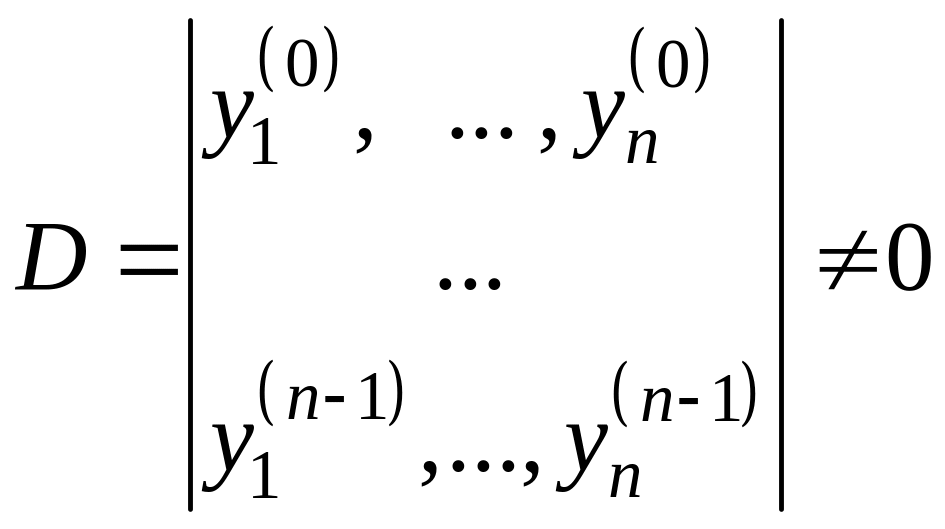 .
Обозначим
.
Обозначим
![]() такие решения (1), для которых
такие решения (1), для которых
![]() .
По свойству 3 с любыми начальными
условиями решение в
существует. Тогда
.
По свойству 3 с любыми начальными
условиями решение в
существует. Тогда
![]() По теореме 2
По теореме 2
![]() линейно независимы, т.е. фундаментальная
система решений.
линейно независимы, т.е. фундаментальная
система решений.
Замечания:
Общего метода для нахождения фундаментальной системы решений не существует.
Каждое (1) имеет бесконечное количество фундаментальных систем решений.
Частный случай (1): когда
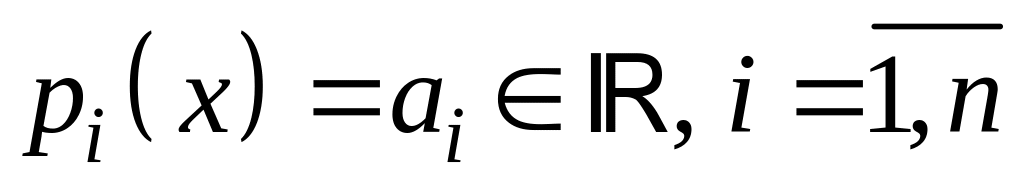 – числа
– числа

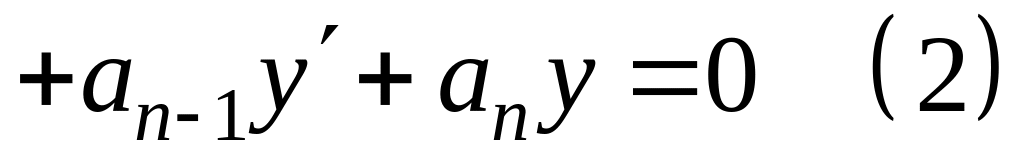
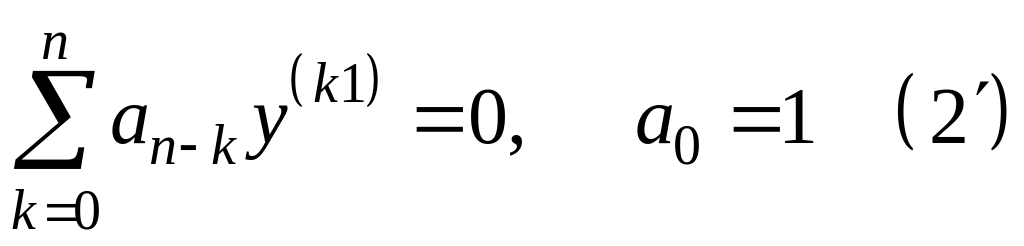
20.Формула общего решения линейного однородного уравнения.
Теорема
5. Формула
общего решения (1) имеет вид:
![]() (3) где
(3) где
![]() – произвольные, принадлежащие
числа, а
– фундаментальная система решений.
– произвольные, принадлежащие
числа, а
– фундаментальная система решений.
Доказательство:
Формула (3) ничего, кроме решений (1) не содержит (т.к. линейная комбинация решений линейного уравнения – решение линейного уравнения).
К любому решению (1) из (3) можно придти. Пусть
 –
любое конкретное решение (1). Выберем
–
любое конкретное решение (1). Выберем
 .
.
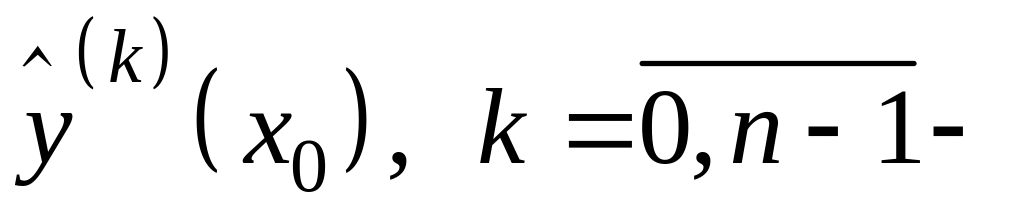 начальное
условие. С такими значениями производных
в точке
существует единственное решение (2)
(т.е.
начальное
условие. С такими значениями производных
в точке
существует единственное решение (2)
(т.е.
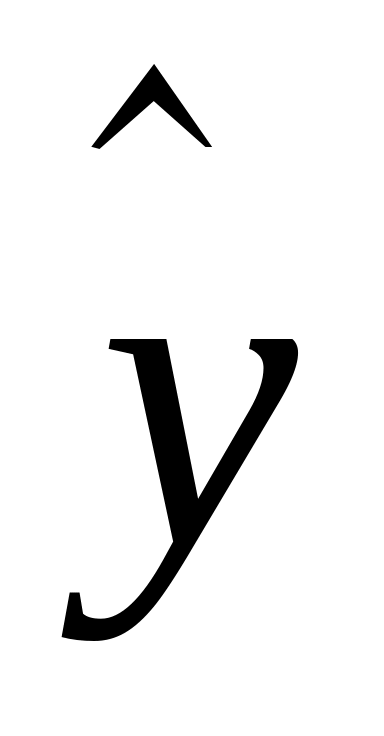 ).
Пусть
).
Пусть
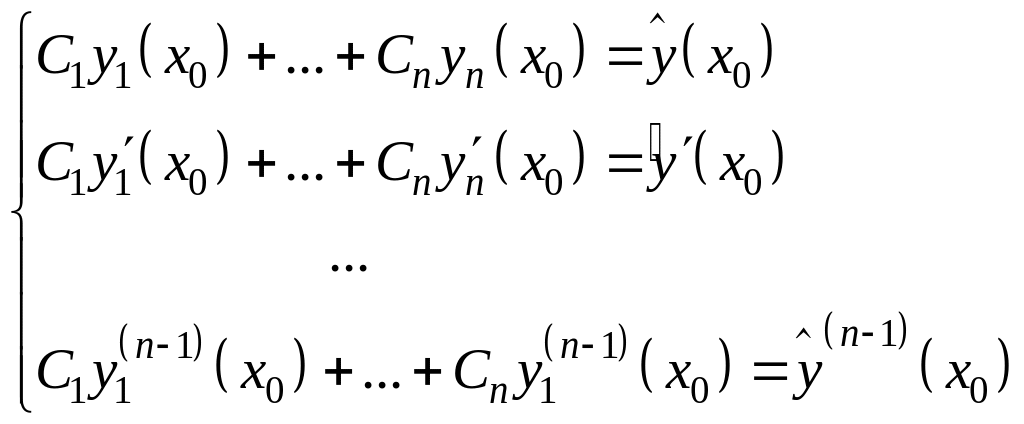 – определитель системы, равный (для
фундаментальной системы решений)
– определитель системы, равный (для
фундаментальной системы решений)
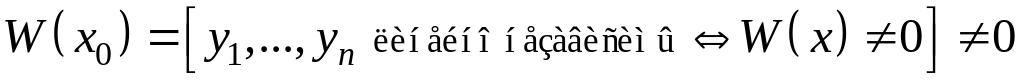
Т.е.
решение (относительно
![]() ).
Находим нужные
.
Тогда (3) – решения (1) с начальными
условиями в точке
и по соответствующему свойству
).
Находим нужные
.
Тогда (3) – решения (1) с начальными
условиями в точке
и по соответствующему свойству
![]() ,
ЧТД.
,
ЧТД.
