
- •1. Основные понятия и факты связанные с д.У.
- •2.Существование, единственность и приближенное решение задачи Коши
- •3. Д.У., описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и д.Р.)
- •4. Приближенное построение интегральных кривых с помощью изоклин.
- •5. Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6. Линейные уравнения 1-ого порядка.
- •7. Уравнение Бернулли и Риккати.
- •8. Уравнения в полных дифференциалах.
- •9. Интегрирующий множитель
- •12. Уравнение Клеро и Лагранжа.
- •13. Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14. Системы д.У. Метод исключения. Общий интеграл.
- •15. Линейные однородные уравнения в частных производных. Задача Коши.
- •16. Квазилинейные уравнения в частных производных. Задача Коши.
- •17. Линейная зависимость функций и вронскиан.
- •18. Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •22.Метод Лагранжа для линейных уравнений.
- •23.Метод неопределенных коэффициентов для линейных уравнений.
- •24.Уравнения Эйлера.
- •25.Линейные однородные системы.
- •26.Линейные однородные системы с постоянными коэффициентами.
- •27. Метод Лагранжа для линейных систем.
- •29.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •31.Устойчивость решений. Система первого приближения. Критерий Рауса-Гурвица.
- •32.Фазовая плоскость. Обоснование одной (любой) из фазовых картин.
- •33.Линейные интегральные уравнения второго рода. Случай вырожденного ядра.
- •34.Задачи вариационного исчисления и понятие о способах их решения.
- •1. Основные понятия и факты связанные с д.У(1)
- •2.Существование, единственность и приближенное решение задачи Коши(2)
22.Метод Лагранжа для линейных уравнений.
I. Метод Лагранжа (метод вариации производных):
1.
![]() ф.с.р
ф.с.р
![]() .
.
2. Записать и решить следующую систему алгебраических уравнений:
!!В исходном уравнении перед производной
высшего порядка должна стоять 1!!, иначе
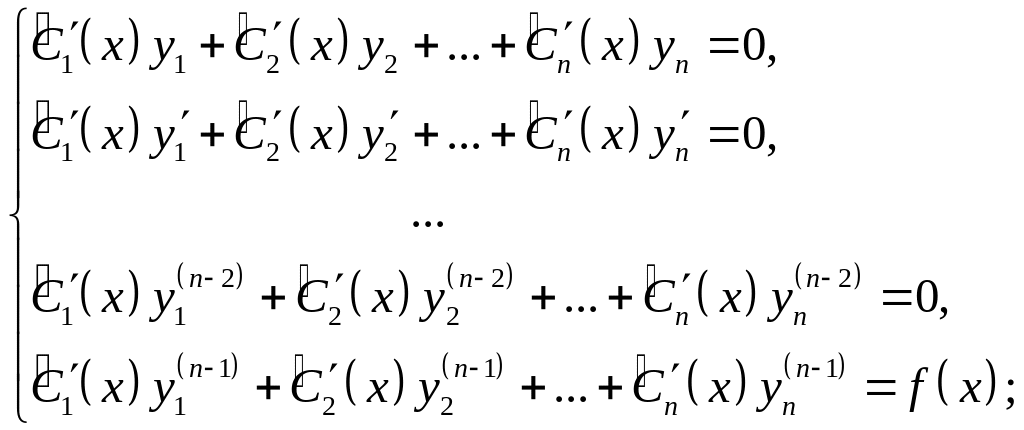
![]() найдется неправильно!
найдется неправильно!
![]() Решаем систему и
находим
Решаем систему и
находим
![]() .
.
![]() (т.к.
(т.к.
![]() фундаментальная
система решений), т.е.
решение. (Задача Коши – просто подставляем
и находим
фундаментальная
система решений), т.е.
решение. (Задача Коши – просто подставляем
и находим
![]() ).
).
![]() .
.
3.
![]() .
.
Доказательство:
 Надо
показать, что
Надо
показать, что
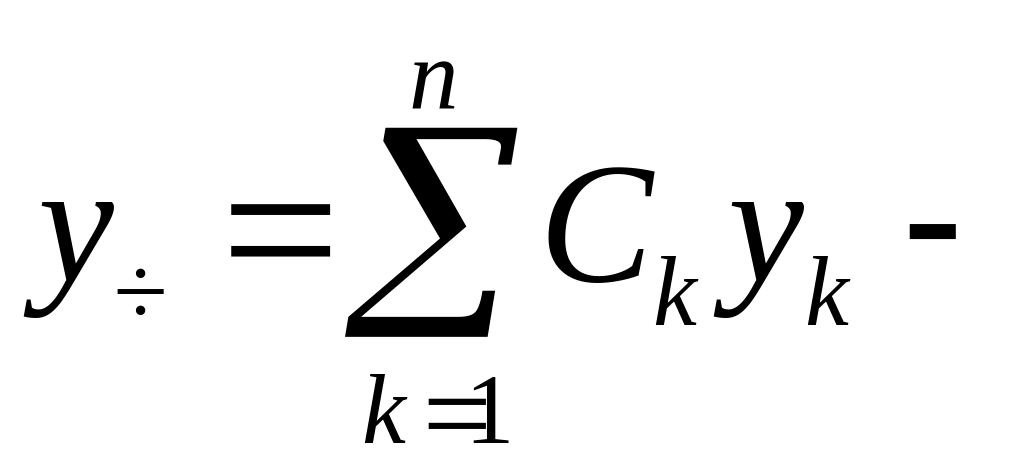 частное
решение (1).
частное
решение (1).
Т.к. первое уравнение
системы, а
Т.к. второе уравнение
системы![]() удовлетворяет
системе
удовлетворяет
системе

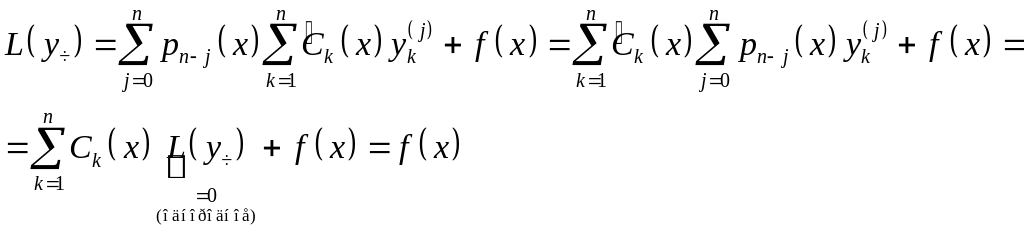
23.Метод неопределенных коэффициентов для линейных уравнений.
![]() .
.
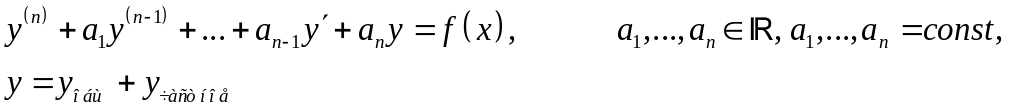
Применяется для любых .
1.
 ;
;

![]() ,
если
,
если
![]() не является корнем соответствующего
характеристического уравнения, иначе
не является корнем соответствующего
характеристического уравнения, иначе
![]() равно кратности
.Сначала
равно кратности
.Сначала
![]() не определены. После подстановки
не определены. После подстановки
![]() в исходное уравнение они находятся.
Известно, что всегда
найдется
и притом единственным образом.
в исходное уравнение они находятся.
Известно, что всегда
найдется
и притом единственным образом.
Пример:
![]()
![]()
![]() сразу
в ответе.
сразу
в ответе.
![]() Тогда
Тогда
![]()
![]()
![]()
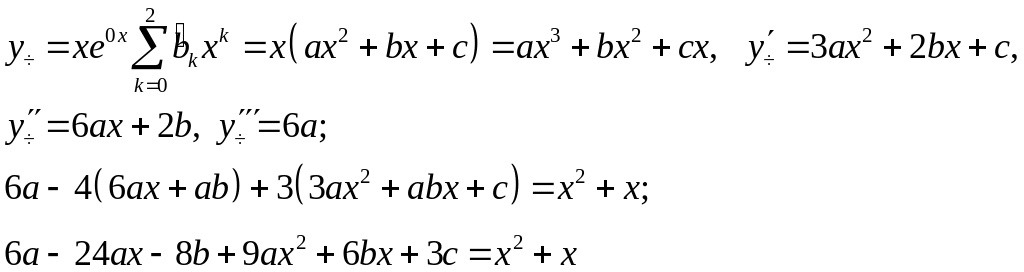
![]()

Ответ:
![]() .
.
2)
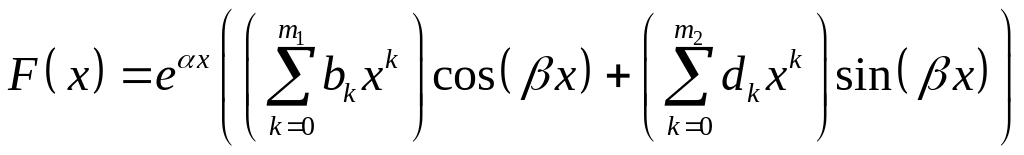
![]()
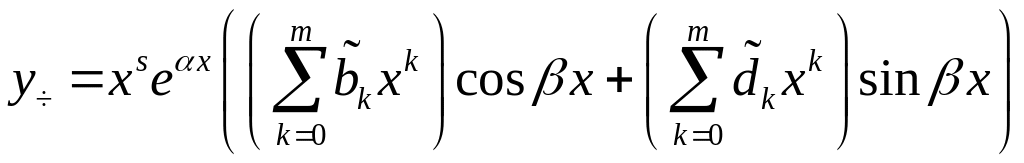 .
.
,
если
![]() ― не корни соответствующего
характеристического уравнения,
равно кратности этих корней.
― не корни соответствующего
характеристического уравнения,
равно кратности этих корней.
![]() Сначала
Сначала
![]() ― неизвестные. Находятся подстановкой
в исходное уравнение.
― неизвестные. Находятся подстановкой
в исходное уравнение.
24.Уравнения Эйлера.
![]()
![]()
![]()
Т.е.
― линейное неоднородное уравнение с
особыми
![]() .
.
![]() ― важен интервал.
Тогда можно
разделить на
― важен интервал.
Тогда можно
разделить на
![]() .
.
Однородное уравнение Эйлера:
![]()
Определение: Определяющее уравнение для однородного уравнения
Эйлера ― следующее:
![]()
― многочлен степени
относительно
![]() .
.
![]() линейного однородного
уравнения надо знать фундаментальную
систему решений.
линейного однородного
уравнения надо знать фундаментальную
систему решений.
Теорема:
Для того, чтобы найти фундаментальную
систему решений
,
надо найти корни соответствующего
уравнения
вместе с их кратностями. Далее каждому
корню
![]() следует сопоставить функции:
следует сопоставить функции:
![]() ,
где
,
где
![]() ― кратность
― кратность
![]() .
.
Каждой паре
комплексных сопряженных корней
уравнения
![]() следует сопоставить функции
следует сопоставить функции
![]()
![]()
где
![]() ― кратность корней
.
― кратность корней
.
Фундаментальную
систему решений
образуют функции, сопоставленные
указанным образом всем
корням
и всем парам
![]() корней
.
корней
.
25.Линейные однородные системы.

![]()
![]() ― коэффициенты
системы
― коэффициенты
системы
![]() определены и
определены и
![]() ― свободные члены
системы
― свободные члены
системы
![]() непрерывны на
непрерывны на
![]() .
.
Если
![]() , то система однородна, иначе ―
неоднородна.
, то система однородна, иначе ―
неоднородна.
 дифференцирование
матрицы ― поэлементно.
дифференцирование
матрицы ― поэлементно.
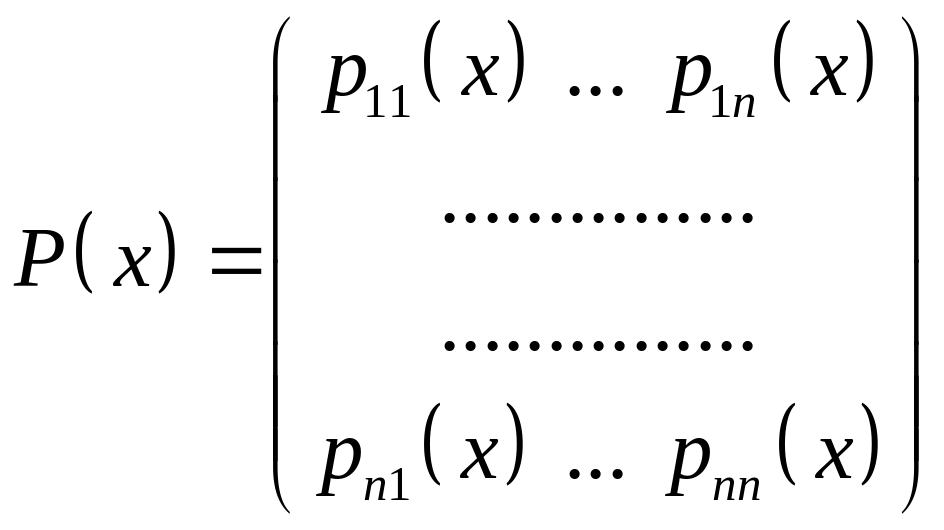 ― матрица системы
― матрица системы
 .
.
Тогда
![]()
Если
![]() ,
то
однородная.
,
то
однородная.
![]() ― однородная.
― однородная.
![]() ― неоднородная.
― неоднородная.
Начальные условия:
![]()
![]() .
.
Свойство:
![]() решение задачи Коши.
.
решение задачи Коши.
.
Определение:
1.
![]() ― линейно зависимы на
,
если
― линейно зависимы на
,
если
![]() ,
не все равные нулю, что
,
не все равные нулю, что
![]() .
.
Если лишь при всех , то линейно независимы.
2. Определитель
Вронского(вронскиан) для


3. Фундаментальная система решений ― совокупность линейно независимы вектор-столбцов, являющихся решением .
4.
Фундаментальная матрица
― матрица, столбцы которой образуют
фундаментальную систему решений
.
Обозначается
![]() .
.
Теоремы:
Пусть
 линейно зависимы. Тогда
линейно зависимы. Тогда
 .
.― решения и
 линейно независимы.
линейно независимы.―решения . Тогда справедливо ровно одно из следующих утверждений:
а.
![]()
б.
![]()
4. системы фундаментальная система решений.
5. Формула общего решения имеет вид:
![]() , где
, где
![]() ― фундаментальная
система решений.
― фундаментальная
система решений.
