
- •1. Основные понятия и факты связанные с д.У.
- •2.Существование, единственность и приближенное решение задачи Коши
- •3. Д.У., описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и д.Р.)
- •4. Приближенное построение интегральных кривых с помощью изоклин.
- •5. Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6. Линейные уравнения 1-ого порядка.
- •7. Уравнение Бернулли и Риккати.
- •8. Уравнения в полных дифференциалах.
- •9. Интегрирующий множитель
- •12. Уравнение Клеро и Лагранжа.
- •13. Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14. Системы д.У. Метод исключения. Общий интеграл.
- •15. Линейные однородные уравнения в частных производных. Задача Коши.
- •16. Квазилинейные уравнения в частных производных. Задача Коши.
- •17. Линейная зависимость функций и вронскиан.
- •18. Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •22.Метод Лагранжа для линейных уравнений.
- •23.Метод неопределенных коэффициентов для линейных уравнений.
- •24.Уравнения Эйлера.
- •25.Линейные однородные системы.
- •26.Линейные однородные системы с постоянными коэффициентами.
- •27. Метод Лагранжа для линейных систем.
- •29.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •31.Устойчивость решений. Система первого приближения. Критерий Рауса-Гурвица.
- •32.Фазовая плоскость. Обоснование одной (любой) из фазовых картин.
- •33.Линейные интегральные уравнения второго рода. Случай вырожденного ядра.
- •34.Задачи вариационного исчисления и понятие о способах их решения.
- •1. Основные понятия и факты связанные с д.У(1)
- •2.Существование, единственность и приближенное решение задачи Коши(2)
15. Линейные однородные уравнения в частных производных. Задача Коши.
![]()
Линейные однородные уравнения
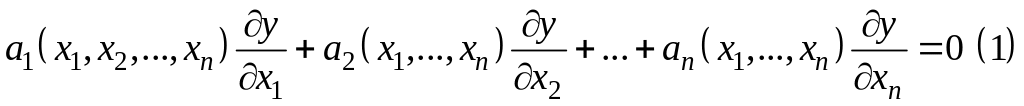
![]() определены в
определены в
![]() хотя бы одно
хотя бы одно
![]() .
Пусть
.
Пусть
![]() .
.
Определение: Системой в симметрической форме, соответствующей уравнению (1), называется система дифференциальных уравнений следующего вида:
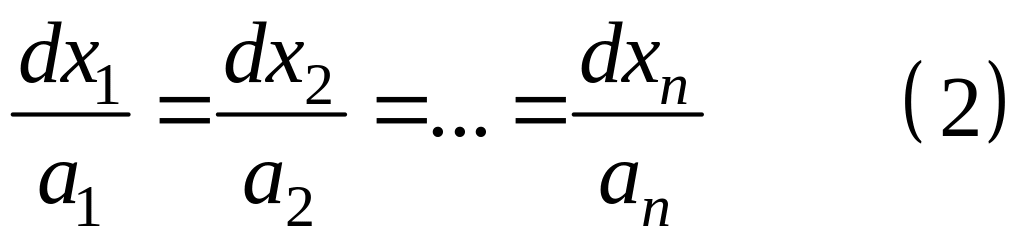
Придадим ей
следующий вид: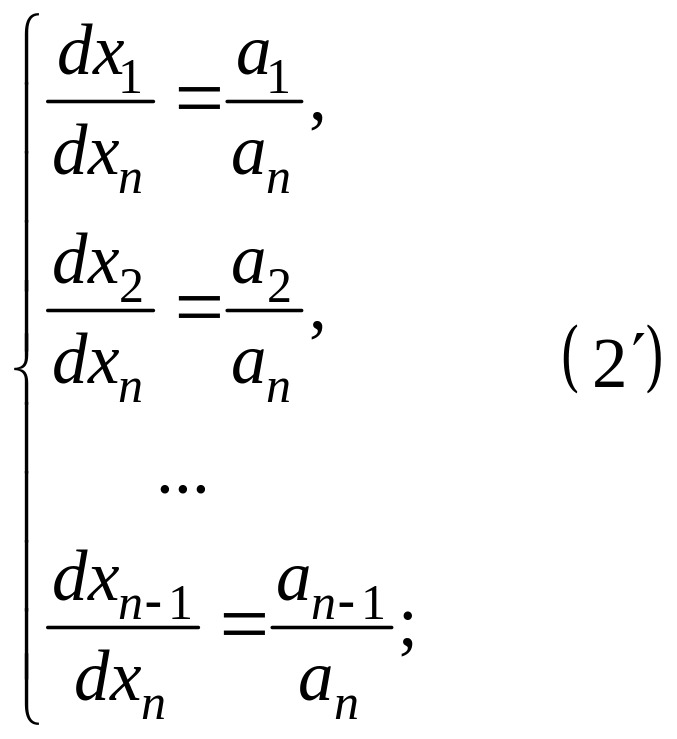
Теорема
1: Для
того, чтобы
![]() была решением (1), необходимо и достаточно,
чтобы
была интегралом (2).
была решением (1), необходимо и достаточно,
чтобы
была интегралом (2).
Док-во:
Пусть – интеграл (2) или (2’), тогда по определению
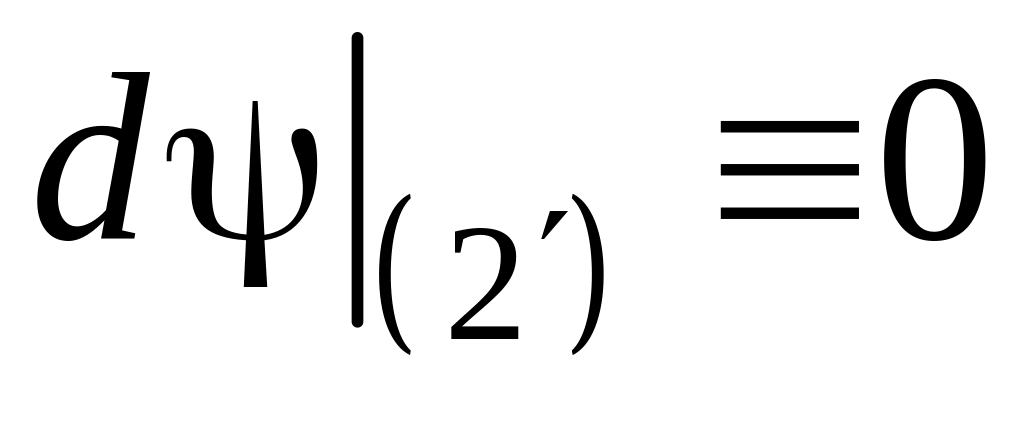 .
.

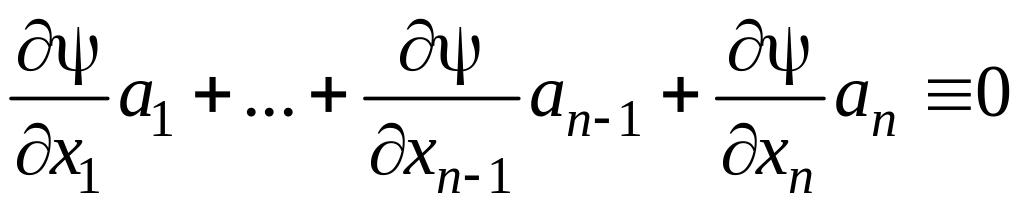 .
По определению,
– решение уравнения (1).
.
По определению,
– решение уравнения (1).
Те же рассуждения, но в другом порядке.
Теорема
2: Формула
общего решения (1) имеет вид
![]() ,
где
,
где
![]() – независимые интегралы системы (2), а
– произвольная дифференцируемая
функция.
– независимые интегралы системы (2), а
– произвольная дифференцируемая
функция.
Док-во:
[Определение: Формула общего решения любого уравнения – такая формула, которая ничего иного, кроме решений, не содержит и по которой к любому решению можно придти].
Ничего иного не содержит
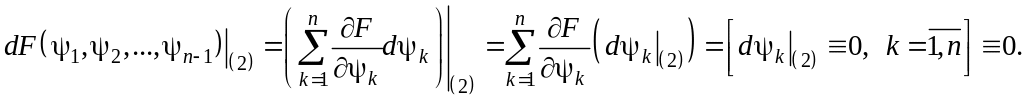
Т. е. ничего, кроме решений, (3) не дает.
2)
![]() произвольное зафиксированное решение
(1). Покажем, что для
произвольное зафиксированное решение
(1). Покажем, что для
![]()
Произвольным
образом возьмем и
зафиксируем
Т.
к.
вует
ненулевое решение.
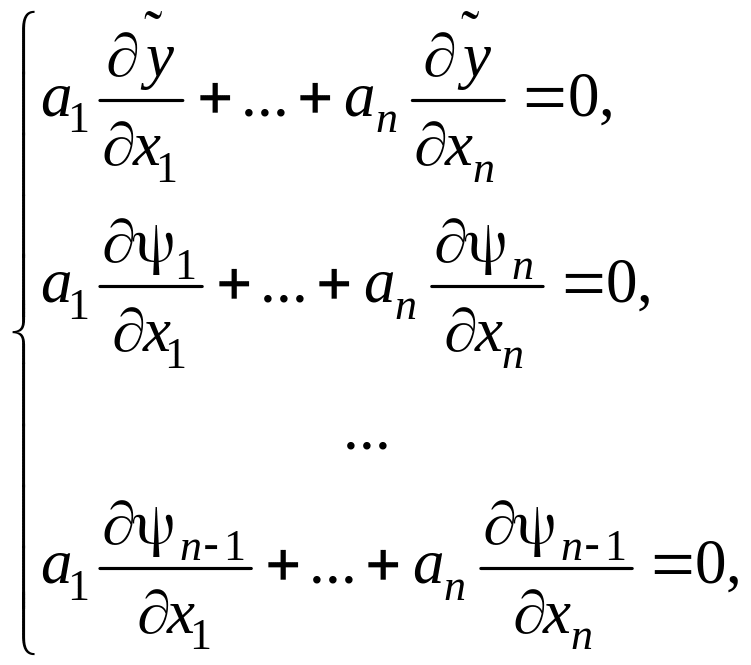
![]() .
.![]() то у системы сущест-
то у системы сущест-
Т. к. есть еще нулевое решение, то (т. к. более одного решения) детерминант системы равен нолю.
Это Якобиан. Если
он тождественно равен нолю, то функции
зависимы, т. к.
а
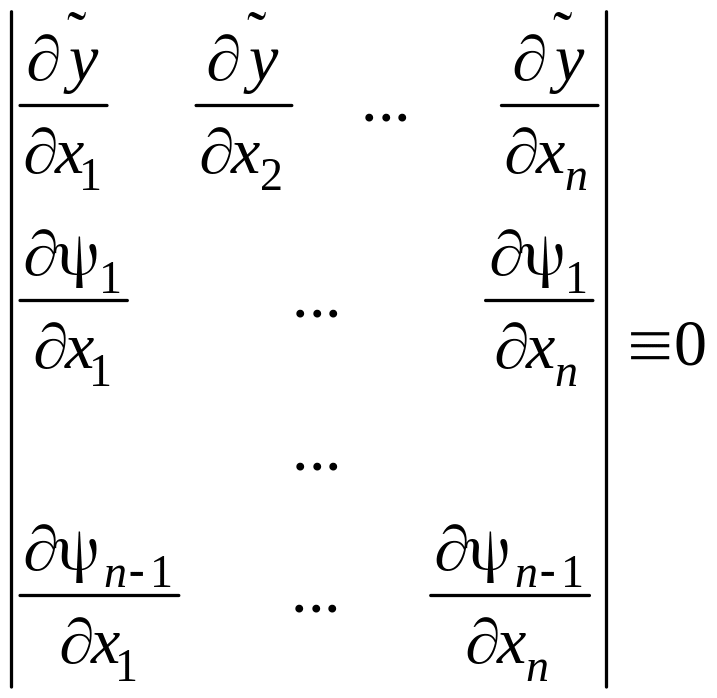
![]() независимы, то
независимы, то
![]() такое, что
такое, что
![]() ,
,![]() дифференцируемо.
дифференцируемо.
16. Квазилинейные уравнения в частных производных. Задача Коши.
Квазилинейные уравнения.
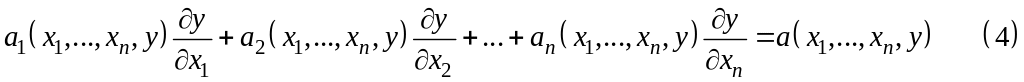 Решать
будем в неявном виде
Решать
будем в неявном виде
![]()
Продифференцируем
(5) по
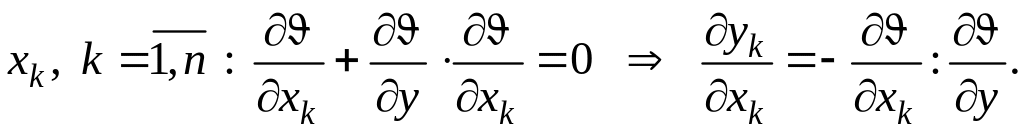
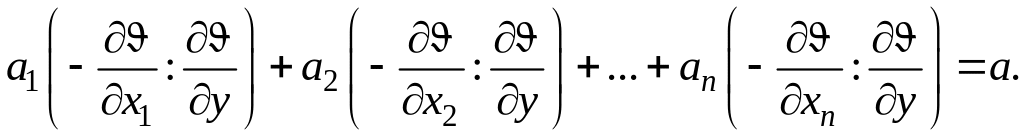
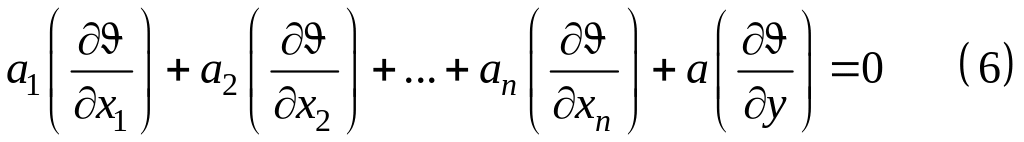
Решив (6), найдем
![]() она и будет решением. Общее решение
уравнения (4):
она и будет решением. Общее решение
уравнения (4):
![]() ,
где
,
где
![]() произвольная дифференцируемая функция,
произвольная дифференцируемая функция,
![]() независимый интеграл системы в
симметричной форме, соответствующей
(6).
независимый интеграл системы в
симметричной форме, соответствующей
(6).
Определение:
Начальное условие для (1) и (4) –
следовательно, дополнительное условие:
![]() ,
,
![]() наперед заданное
число, принадлежащее
наперед заданное
число, принадлежащее
![]() ,
,
![]() наперед заданная функция.
наперед заданная функция.
(1), (8) или (4), (8) – задача Коши.
Схема решения этих задач:
(1), (8):
1) находим независимые интегралы соответствующей системы в симметричной форме (2).
2
функции![]() находим эти
находим эти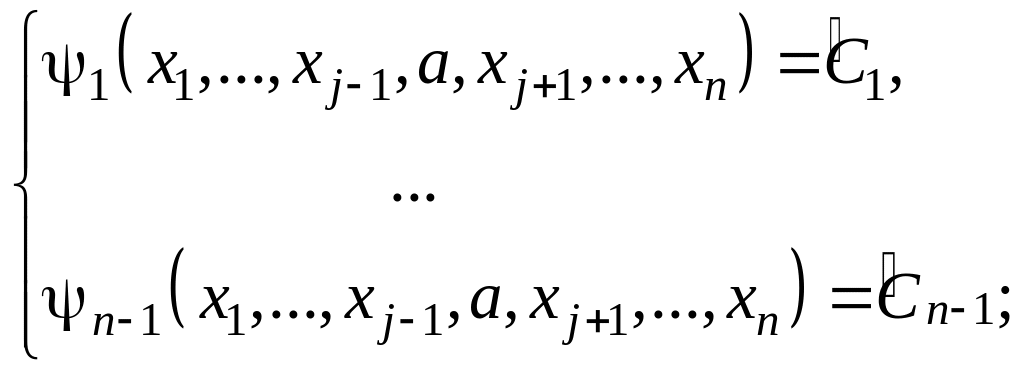 Надо решить эту систему
Надо решить эту систему
![]()
![]()
3)
![]()
II (4), (8):
1)
![]() – независимые интегралы системы в
симметричной форме, соответствующей
уравнению (6).
– независимые интегралы системы в
симметричной форме, соответствующей
уравнению (6).
2) Составить и решить:
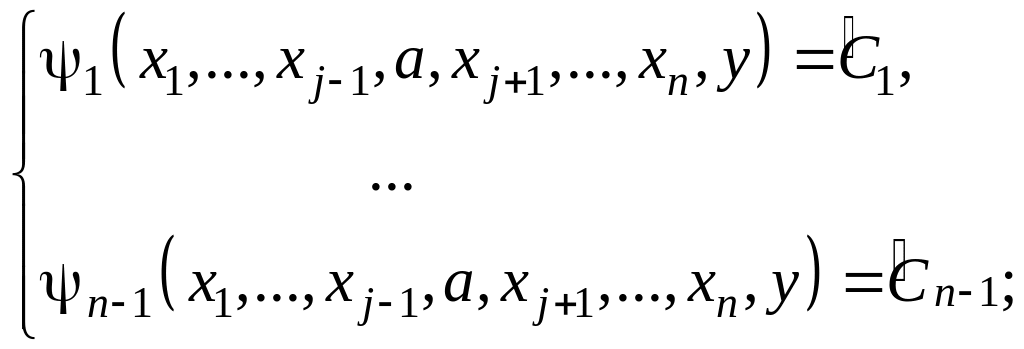
![]() ,
,
![]() ,
находим эти функции:
,
находим эти функции:
![]()
3)
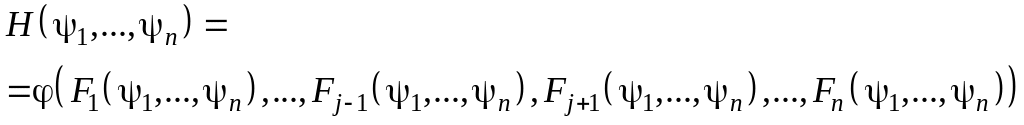
17. Линейная зависимость функций и вронскиан.
Определение:
Функции
![]() ,
определенные на интервале
,
определенные на интервале
![]() ,
называются линейно зависимыми на
,
если
,
называются линейно зависимыми на
,
если
![]() не все равные нолю, такие что
не все равные нолю, такие что
![]() Если же тождество справедливо лишь при
Если же тождество справедливо лишь при
![]() ,
то функции линейно независимы.
,
то функции линейно независимы.
Определение:
Определитель Вронского
![]() раз дифференцируемых функций
раз дифференцируемых функций
![]() следующий определитель
следующий определитель
![]() :
:

![]()
Теорема:
Если
![]() линейно зависимы и
линейно зависимы и
![]() на
,
то
на
,
то
![]() .
.
Док-во: Т. к. функции
линейно зависимы, то
![]() не все равные нолю,
не все равные нолю,
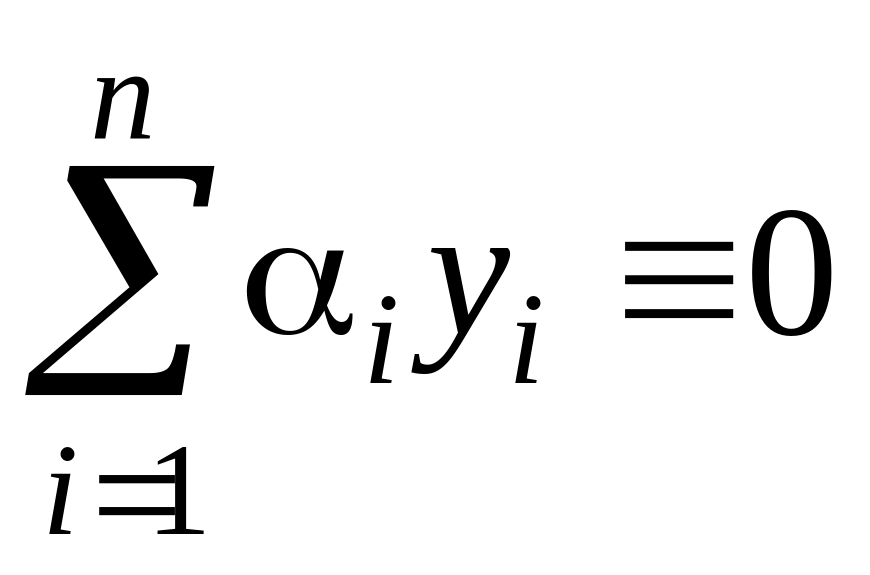 .
Дифференцируем.
.
Дифференцируем.
 .
Зафиксируем
.
Зафиксируем
![]() .
Тогда
.
Тогда
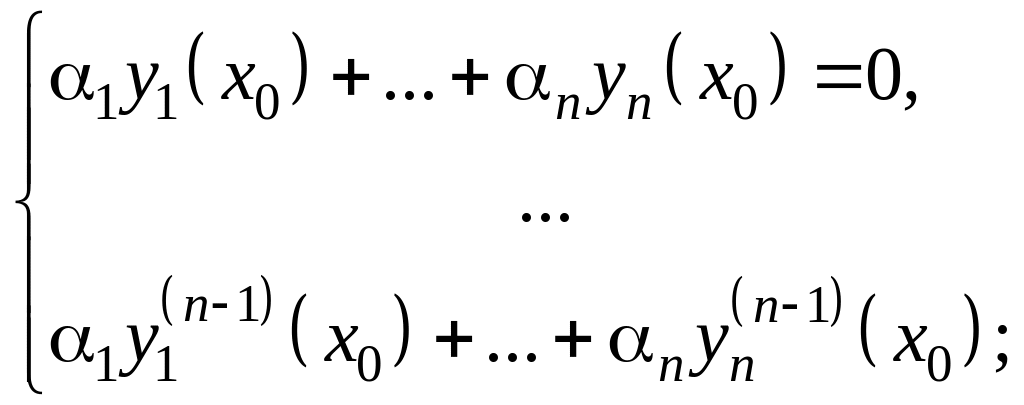 Рассмотрим эту линейную систему как
систему от
Рассмотрим эту линейную систему как
систему от
![]() .
Тогда у нее (по условию не все
.
Тогда у нее (по условию не все
![]() )
существует нетривиальное решение. См.
предыдущую лекцию.
)
существует нетривиальное решение. См.
предыдущую лекцию.
![]() системы равен нолю, а
системы равен
.
системы равен нолю, а
системы равен
.
![]() .
Т. к.
.
Т. к.
![]() производная, то
.
производная, то
.
Следствие:
![]()
![]() линейно независимы.
линейно независимы.
Доказательство проводим от противного.
Примеры линейно зависимых функций:
1)
![]() линейно зависимы
линейно зависимы
![]() .
.
2) Если
![]() то функция
линейно
зависима для
то функция
линейно
зависима для
![]()
![]() .
.
Примеры линейно независимых функций:
1)
![]() линейно независимы для
линейно независимы для
![]() .
Многочлен степени не выше
не может иметь более
корней, а на отрезке
число точек равно бесконечности. Поэтому
линейно независимы.
.
Многочлен степени не выше
не может иметь более
корней, а на отрезке
число точек равно бесконечности. Поэтому
линейно независимы.
Следствие:
Многочлены равны
![]() равны коэффициенты при одинаковых
степенях
.
равны коэффициенты при одинаковых
степенях
.

Тогда
![]()
2)
линейно независимы
![]() ,
где
,
где
![]() попарно неравные.
попарно неравные.
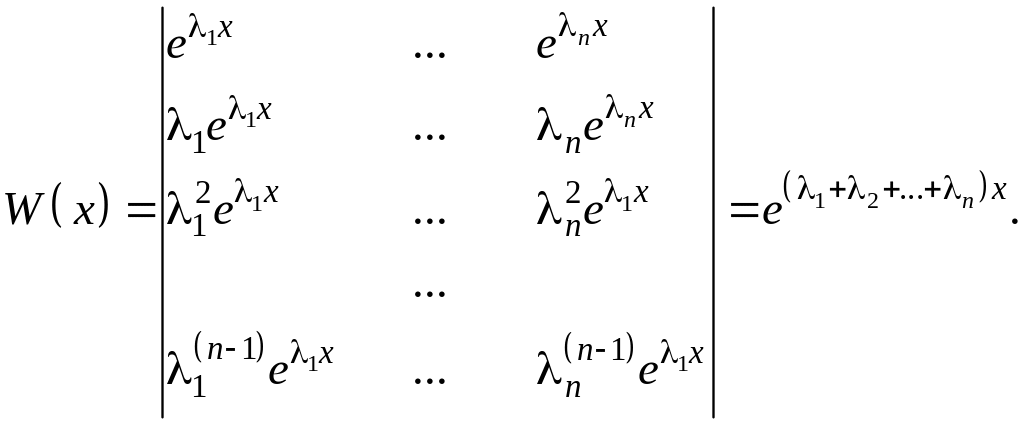
 [определитель
Вандермонда – из произведений разностей
[определитель
Вандермонда – из произведений разностей
![]() .
Т. к. они попарно различны, то он не равен
нолю;
.
Т. к. они попарно различны, то он не равен
нолю;
![]() ]
]![]() .
По следствию из теоремы
.
По следствию из теоремы
![]() линейно независимы.
линейно независимы.
3)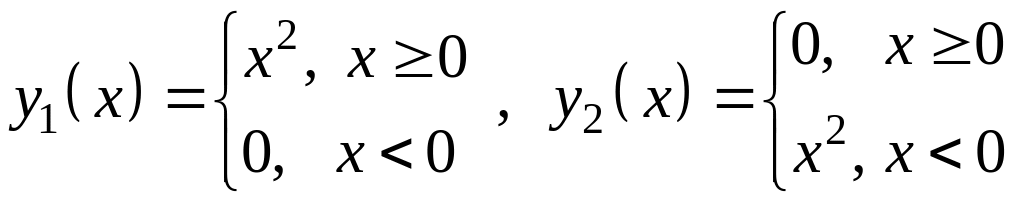
![]()
![]() т.е
т.е
![]() линейно независимы.
линейно независимы.
Запишем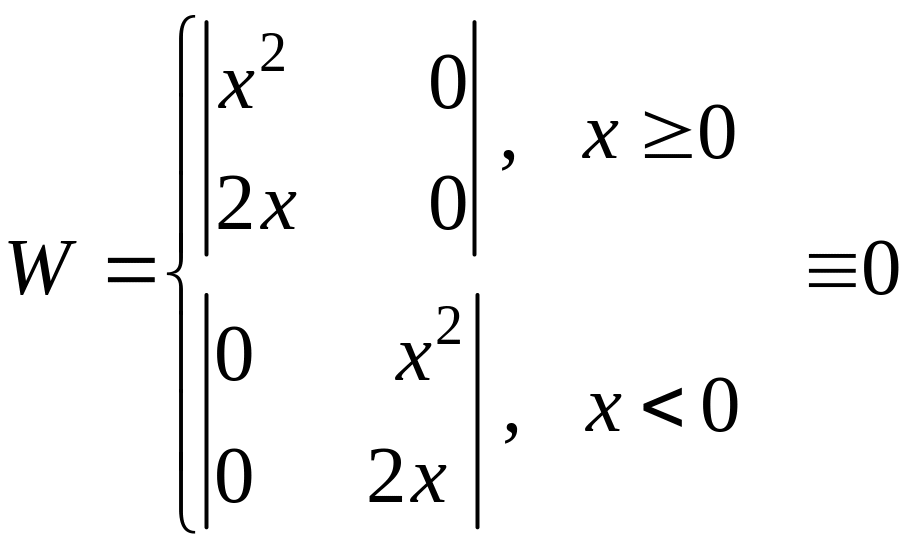 ,
т.е. теорема не верна в обратную сторону!!!
,
т.е. теорема не верна в обратную сторону!!!
4)
линейно независимы
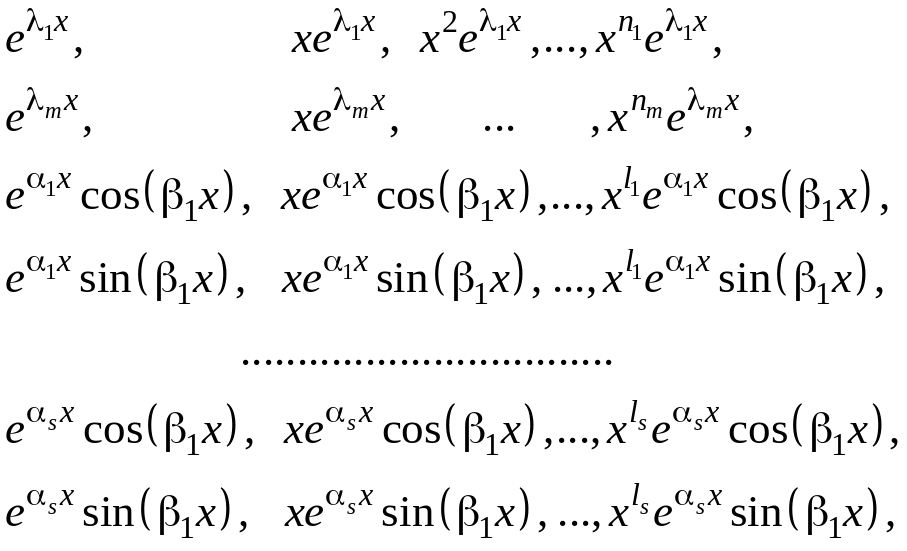
Все
![]() ;
Все
;
Все
![]() .
.
![]() попарно различны.
попарно различны.
![]() ;
;
![]() попарно различны (т.е. различны оба
числа). (Без доказательства)
попарно различны (т.е. различны оба
числа). (Без доказательства)
