1. Понятие события в теории вероятностей, вероятность события, достоверное событие, невозможное событие. Классическая формула вычисление вероятности (схема «случаев»), частотная интерпретация вероятности (свойство устойчивости частот).

Теория вероятностей – матем. наука, изучающая закономерности случайных явлений (С.Я.).

С. Я. – явление, которое при неоднократном повторении одного и того же опыта протекает каждый раз по-иному.

Событие – факт, который в результате опыта может произойти или не произойти. (А = {появление герба при подбрасывании монеты}, В = {появление трех гербов при 3кратном подбрасывании}.

Вероятность события – числовая хар-ка степени возможности появления какого-либо случайного события при тех или иных условиях. Р(А).

Достоверное событие – событие, вероятность которого равна 1; это то событие, которые обязательно произойдет. Р(Ω)=1 (выпадение не более 6 очков при подбрасывании играл. кубика). Недостоверное – вероятность меньше 1.

Невозможное событие – вероятность равна 0. Р(Ø)=0.

Классическая формула вычисление вероятности: P=m_A/n, где n – общее число случаев, m_A — число случаев, благоприятных событию А (обеспечивающих его появление). Здесь предполагается, что элементарные исходы не совместны, равновозможные и образуют полнeую группу:

- события называются несовместными, если никакие 2 из них не могут появиться вместе (выстреле - попад/промах)

- несколько событий наз-ся равновозможными, если по условию симметрии можно считать, что ни одной из этих событий не является объективно более возможным, чем другое (выпадение любого числа от 1 до 6 при подбрасывании кубика)

- несколько события образуют полную группу, если в результате опыта должно появиться хотя бы одно из них (появление 1,2,3,4,5,6 очков при подбрасывании; хотя бы 1 промах и хотя бы 1 попадание при 2 выстрелах)

Частота события в серии из N опытов – отношение числа опытов, в которых это событие произошло, к общему числу произведенных опытов. Р*(А)=m/n

Частоту события иначе называют его статистической вероятностью. Именно статистика массовых случайных явлений — база для определения вероятностей событий в опытах, не обладающих симметрией возможных исходов.

Случайные обстоятельства, сопровождающие каждый отдельный опыт, в массе опытов взаимно погашаются, и частота постепенно стабилизируется, приближаясь, с незначительными колебаниями, к некоторой средней, постоянной величине.

Свойство устойчивости частот при большом числе однородных опытов – одна из наиболее характерных закономерностей, наблюдаемых в массовых С.Я. Если мы повторяем (воспроизводим) один и тот же опыт много раз (причем обеспечена независимость исходов отдельных опытов), частота события становится все менее случайной, выравнивается, приближается к постоянной.

2. Алгебра событий. Основные операции над событиями. Теорема сложения вероятностей. Следствия.

С каждым испытанием связан ряд интересующих нас событий, которые, вообще говоря, могут появляться одновременно. Например, при бросании игральной кости событие А есть выпадение двойки, а событие В – выпадение четного числа очков. Очевидно, что эти события не исключают друг друга.

Для упрощения записи и возможности логического построения рассуждений в теории вероятностей вводятся операции над событиями. И на их основе строится алгебра событий.

А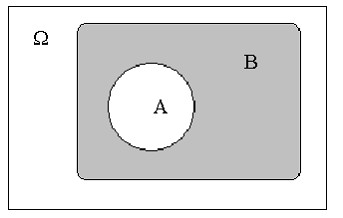 лгебра событий – алгебра подмножеств пространства элементарных событий, элементами которого служат элементарные события.

Отношение следования А⊂В – событие А влечет за собой В

Эквивалентность А=В – А и В тождественны, неотличимы

С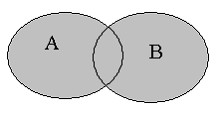 умма двух событий А и В – событие С, состоящее в выполнении события А или события В или обоих вместе. (А+В – награждение победителя или призом, или премией, или обоими)

П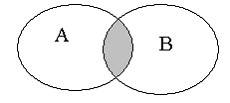 роизведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий. Если А, В, С – совместные события, то их произведение АВС называется событие, состоящее в совместн. наступлении всех этих событий. (АВС – награждение премией, призом и медалью одновременно)

Р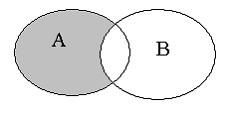 азностью А-В двух событий называется событие, которое состоится, если событие А произойдет, а событие В нет. (АВ-С – награждение одновременно призом и премией без выдачи медали)

Свойства операций сложения и умножения событий:

1. А+В = В+А – коммутативность сложения

2. А+(В+С)=(А+В)+С – ассоциативность сложения

3. АВ=ВА – коммутативность умножения

4. А(ВС) = (АВ)С – ассоциативность сложения

5. А(В+С) = АВ+АС; А+ВС = (А+В)(А+С) – з. дистрибутивности

Из опр-я опций над соб-ми вытекают очевид. неравенства:

А+А=А, АА=А, А+Ω=Ω, АΩ=А, А+Ø=А, АØ= Ø.

Теорема сложения вероятностей – вероятность суммы двух несовместных событий равны сумме вероятностей этих событий: P(A+B) = P(A) + P(B).

Доказательство. Введем обозначения: n- число возможных элементарных исходов событий, m₁ – число исходов благоприятствующих событию А, m₂ – событию В. Число элементарных исходов, благоприятствующих наступлению либо А, либо В, тогда P(A+B) = (m₁+m₂)/n = m₁/n+m₂/n = P(A) + P(B).

Следствие 1: Если события А₁,...,А_m образуют полную группу несовместных событий, то сумма их вероятностей = 1.

Противоположными называются два несовместных события, образующие полную группу. Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. P(A+B) = P(A) + P(B) – P(AB), где Р(АВ) – вер-ть одноврем. наступления и события А, и соб. В.

Следствие 2: Сумма вероятностей противоположных событий равна единице. P(A) + P(А) = 1.

3. Условная вероятность. Теорема умножения вероятностей. Следствия. Независимость событий.

Вероятность Р(В) как мера степени объективной возможности наступления события В имеет смысл при выполнении определенного комплекса условий. При изменении условий вероятность события В может измениться. Так, если к комплексу условий, при котором изучалась вероятность Р(В), добавить новое условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается Р_А(В), или Р(В/А), или Р(В|А).

Теорема умножения вероятностей – вероятность произведения двух событий равна произведению вероятности его события на условную вероятность второго события при условия, что первое событие произошло. Р(АВ) = Р(А) * Р(В|А).

Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от А.

Следствие 2. Вероятность произведения двух независимых событий равна Р(АВ) = Р(А) * Р(В).

Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого.

Например, кость брошена 2 раза. Вероятность появления 2 при втором бросании не зависит от появления 1 при первом.

Несколько событий называются независимыми, если независимы любые два из них и независимы любое из данных событий и любые комбинации остальных событий. В противном случае события называются зависимыми.

Напр., 3 события А, В и С независимы, если независимы события А и В, А и С, В и С, А и ВС, В и АС, С и АВ.