12. Несобственные интегралы

12.1. Несобственные интегралы с бесконечными пределами

Пусть функция определена на и интегрируема на любом конечном отрезке т.е. при любых существует интеграл:

. Если меняется, то данный интеграл будет функцией переменного верхнего предела и тогда можно говорить о вычислении этой функции.

Определение. Предел интеграла при называется несобственным интегралом функции с бесконечным верхним пределом. Обозначается так:

Если указанный предел существует и конечен, то говорят, что данный несобственный интеграл сходится. Если предел не существует или равен бесконечности, то данный несобственный интеграл расходится.

Пусть теперь определена на и интегрируема на любом конечном отрезке следовательно, существует интеграл

Определение. Предел при называется несобственным интегралом функции с бесконечными пределами снизу.

Обозначается так:

Если указанный предел существует и конечен, то несобственный интеграл сходится. Если предел не существует или равен бесконечности, то несобственный интеграл расходится.

Определение. Несобственный интеграл с бесконечным верхним и бесконечным нижним пределом определяется равенством где а любое число.

Пример. Вычислить:

12.2. Применение формулы Ньютона-Лейбница.

Пусть требуется вычислить несобственный интеграл и пусть известна первообразная для

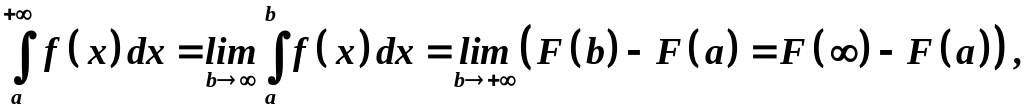т.е. вместо х в первообразной формально подставляют Таким образом, мы можем пользоваться формулой Ньютона-Лейбница.

Аналогично,

Пример.

Иногда, в теории и на практике бывает важно установить, сходится или расходится несобственный интеграл не вычисляя его. Это возможно, благодаря признакам сравнения.

Теорема 1. Пусть две положительные функции, определенные в промежутке причем хотя бы при где Тогда, если сходится, то также сходится. Если расходится, то также расходится.

Теорема 2. Пусть знакопеременная функция, и если сходится, то сходится и интеграл . (Без доказательства).

На практике при исследовании интегралов на сходимость важна функция 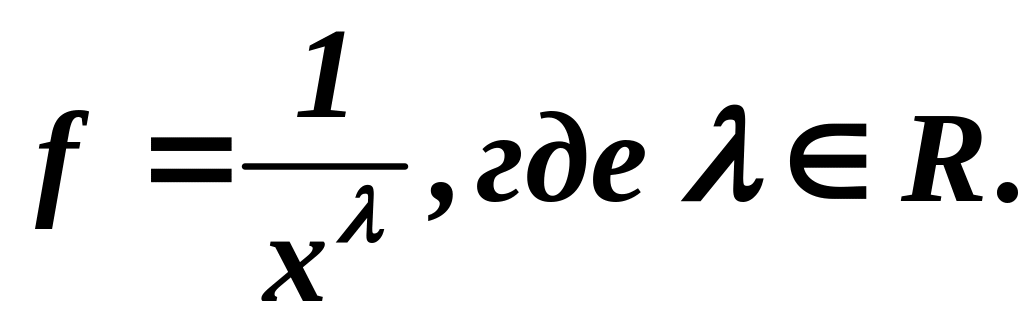Выясним, при каких сходится или расходится интеграл от этой функции.

Пример.

Пусть тогда

Если , то при следовательно интеграл равен бесконечности и он расходится.

Если то при и интеграл сходится.

Если то и интеграл расходится.

Вывод:

Пример. Исследовать на сходимость интеграл: Сделаем оценку сходятся, т.к. . Следовательно, исходный интеграл сходится.

Теоремы (1) и (2) справедливы и для и

12.3. Несобственные интегралы с конечными пределами

Пусть функция определена на но не интегрируема на нем. Предположим, что интегрируема на любом Это значит, существует интеграл: а - не существует. В этом случае точка называется особой точкой функции

Определение: называется несобственным интегралом функции с конечными пределами, т.е.

Если предел существует и конечен, то интеграл называется сходящимся, если предел бесконечен или не существует, то интеграл расходится.

Пример. - особая точка, функция в ней не существует.

Пусть теперь интегрируема на любом и неинтегрируемая на В этом случае точка а - особая и несобственный интеграл определяется так:

Может случиться так, что точки а и b – особые. Тогда

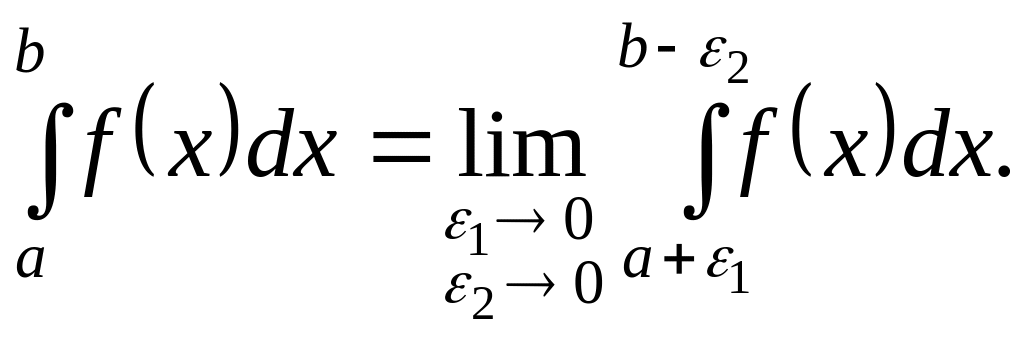
Может оказаться так, что особая точка может оказаться внутри области. С – особая, причем

В этом случае функция интегрируема на и не интегрируема на В данном случае несобственный интеграл вычисляется как предел суммы двух интегралов

Аналогично определяется несобственный интеграл, когда внутри имеется несколько особых точек функции.

Для несобственных интегралов с конечными пределами справедливы теоремы 1, 2.

На практике, при исследовании несобственных интегралов с конечными пределами на сходимость используются функции где Нетрудно проверить, что интегралы сходятся при а расходится при

Пример. Исследовать на сходимость особая. Т.к. на то Рассмотрим - сходится, т.к. Следовательно наш интеграл сходится.