
- •1.2. Понятие неопределенного интеграла и его свойства
- •Свойства неопределенного интеграла
- •1.3. Правила и формулы интегрирования Правила:
- •2. Замена переменной в неопределенном интеграле
- •Алгоритм интегрирования методом замены переменной.
- •3. Интегрирование «по частям» в неопределенном интеграле
- •- Формула интегрирования по частям.
- •Алгоритм нахождения интеграла методом интегрирования по частям.
- •4. Интегрирование выражений, содержащих квадратный трехчлен
- •Интегралы вида ,
- •5. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •6. Интегрирование некоторых иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •8. Определенный интеграл
- •8.1. Понятие определенного интеграла.
- •8.2. Геометрический смысл определенного интеграла
- •8.3. Свойства определенного интеграла
- •8.4. Интеграл как функция переменного верхнего предела
- •8.5. Производная от интеграла по переменному верхнему пределу.
- •8.6. Вычисление определенного интеграла. Формула Ньютона-Лейбница
- •8.7. Замена переменной в определенном интеграле
- •8.8. Интеграл с симметричными пределами от четной и нечетной функции
- •8. 9. Интегрирование «по частям» в определенном интеграле
- •4. Длина дуги кривой и ее дифференциал.
- •Задача о вычислении пути.
- •12. Несобственные интегралы
- •12.1. Несобственные интегралы с бесконечными пределами
- •12.2. Применение формулы Ньютона-Лейбница.
- •12.3. Несобственные интегралы с конечными пределами
8. 9. Интегрирование «по частям» в определенном интеграле
Пусть
![]() и
и
![]() непрерывные на отрезке
функции имеющие непрерывные производные
непрерывные на отрезке
функции имеющие непрерывные производные
![]() .
По правилу дифференцирования произведения
двух функций:
.
По правилу дифференцирования произведения
двух функций:
 Проинтегрируем это равенство на
:
Проинтегрируем это равенство на
:
 .
По формуле Ньютона-Лейбница:
.
По формуле Ньютона-Лейбница:

 т.к.
т.к.
![]()
 Откуда
получаем формулу:
Откуда
получаем формулу:

Пример.

 .
.
9.
Приложения определенного интеграла
1.
Определенный интеграл – есть площадь
криволинейной трапеции,
образованная осью
,
прямыми
 ,
где
,
где
![]() .
.
Е

![]() то
то
![]() Тогда
Тогда

Пример.
Вычислить площадь фигуры, ограниченную
отрезком




 .
.
Выведем формулу для вычисления объема тела, образованного вращением вокруг оси криволинейной трапеции.
П
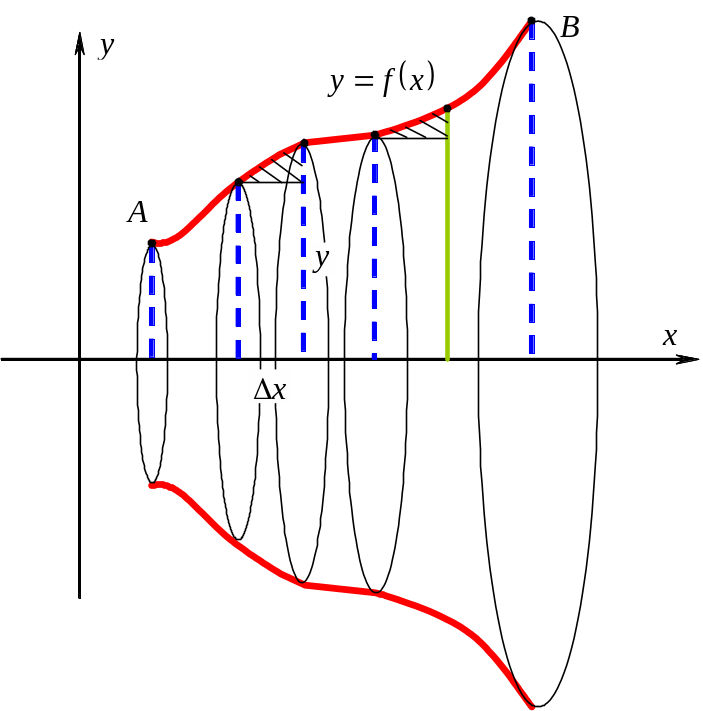
![]()
Тогда, объем каждой части будет складываться из объема тела, образованного вращением прямоугольника с основанием и высотой у и объема тела, образованного вращением криволинейного треугольника, расположенного над прямоугольником (заштриховано серым). При большом разбиении тела плоскостями объем тела, получающегося от вращения треугольника, есть бесконечно малая и ее можно отбросить.
Объем
цилиндра, с радиусом у,
а высотой
равен
![]()

Пример.
Найти объем тела, образованного вращением
эллипса вокруг оси
![]()

Решение. Выразим


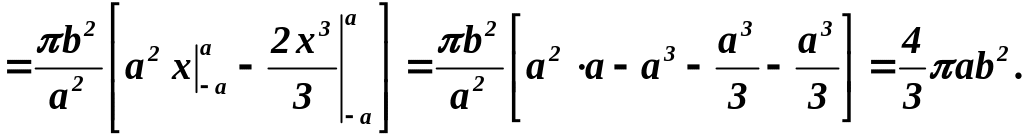
3.
Аналогично, объем
тела,
образованного вращением
вокруг оси
![]() ограниченного кривой
ограниченного кривой
![]() и прямыми
и прямыми
![]() равен
равен
 .
.
4. Длина дуги кривой и ее дифференциал.
Пусть дана кривая АВ уравнение которой
 где
- непрерывно дифференцируемая.
где
- непрерывно дифференцируемая.

Разобьем
отрезок
на
равных частей точками:
 На дуге АВ
получим ломаную из точек
На дуге АВ
получим ломаную из точек
![]() вписанную в дугу. Пусть периметр этой
ломаной равен
вписанную в дугу. Пусть периметр этой
ломаной равен

Определение:
Длиной
дуги АВ
называется
число l,
равное пределу последовательности
периметров:

Определение: Кривая, имеющая длину называется спрямляемой.
Используя
формулу расстояния между точками и
формулу Лагранжа о среднем значении на
отрезке получим:
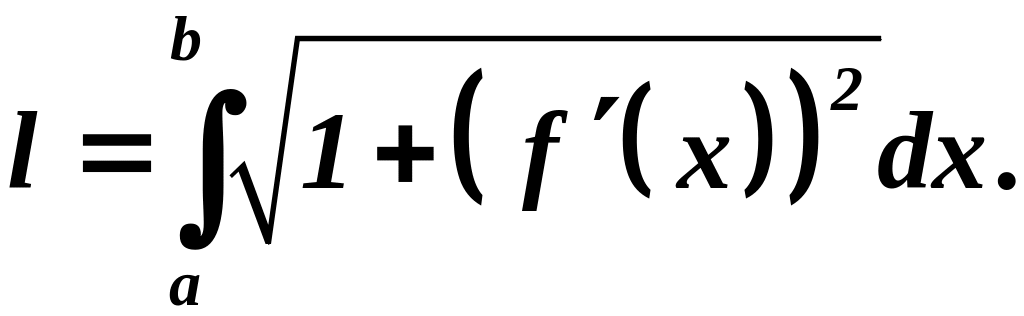
Рассмотрим интеграл от переменного верхнего предела:

Т.к.
подынтегральная функция непрерывна,
то этот интеграл можно дифференцировать

Из
последнего легко получается формула
для дифференциала дуги
 или
или

2)
Пусть кривая задана в параметрическом
виде:
 тогда:
тогда:


Примеры:
1) Вычислить
длину дуги полукубической параболы
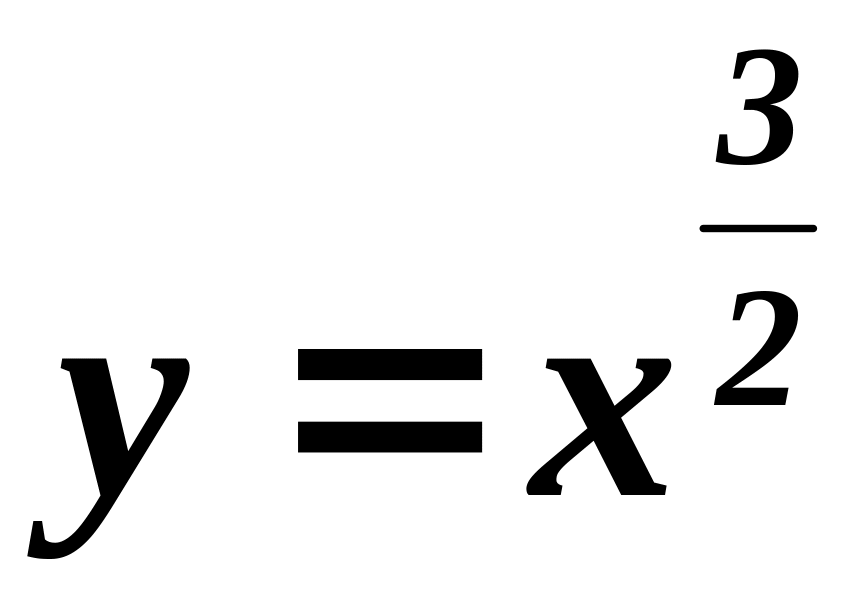 от ее вершины
от ее вершины
![]() до точки
до точки
![]()
Решение:



2)
Вычислить длину одной арки циклоиды
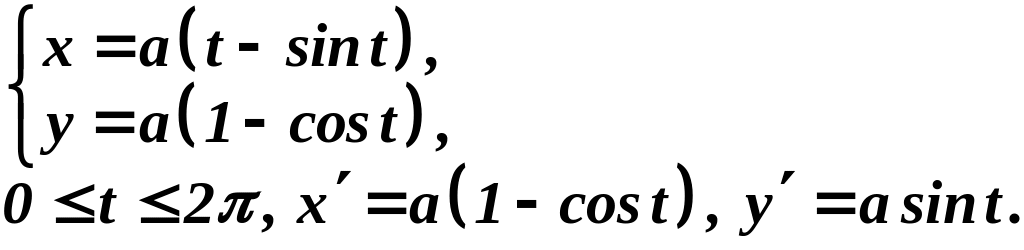
Решение:

Задача о вычислении пути.
Пусть
материальная точка движется прямолинейно
с мгновенной скоростью
![]() Требуется найти путь, который пройдет
тело за промежуток времени от
Требуется найти путь, который пройдет
тело за промежуток времени от
![]() до
до
![]()
Если
скорость постоянная, то
![]() т.е.
т.е.
 В общем случае,
В общем случае,

Пример.
Тело движется прямолинейно со скоростью
![]() м/с. Найдите а,
если известно, что путь, пройденный
телом за 2с. от начала движения равен 48
м.
м/с. Найдите а,
если известно, что путь, пройденный
телом за 2с. от начала движения равен 48
м.
Решение.

![]()
![]()
![]()
Ответ:
![]()
