
- •1.2. Понятие неопределенного интеграла и его свойства
- •Свойства неопределенного интеграла
- •1.3. Правила и формулы интегрирования Правила:
- •2. Замена переменной в неопределенном интеграле
- •Алгоритм интегрирования методом замены переменной.
- •3. Интегрирование «по частям» в неопределенном интеграле
- •- Формула интегрирования по частям.
- •Алгоритм нахождения интеграла методом интегрирования по частям.
- •4. Интегрирование выражений, содержащих квадратный трехчлен
- •Интегралы вида ,
- •5. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •6. Интегрирование некоторых иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •8. Определенный интеграл
- •8.1. Понятие определенного интеграла.
- •8.2. Геометрический смысл определенного интеграла
- •8.3. Свойства определенного интеграла
- •8.4. Интеграл как функция переменного верхнего предела
- •8.5. Производная от интеграла по переменному верхнему пределу.
- •8.6. Вычисление определенного интеграла. Формула Ньютона-Лейбница
- •8.7. Замена переменной в определенном интеграле
- •8.8. Интеграл с симметричными пределами от четной и нечетной функции
- •8. 9. Интегрирование «по частям» в определенном интеграле
- •4. Длина дуги кривой и ее дифференциал.
- •Задача о вычислении пути.
- •12. Несобственные интегралы
- •12.1. Несобственные интегралы с бесконечными пределами
- •12.2. Применение формулы Ньютона-Лейбница.
- •12.3. Несобственные интегралы с конечными пределами
3. Интегрирование «по частям» в неопределенном интеграле
Пусть
функции
![]() имеют непрерывные производные
имеют непрерывные производные
![]() .
По правилу дифференцирования произведения
двух функций, имеем:
.
По правилу дифференцирования произведения
двух функций, имеем:
![]()
Откуда
![]() .
Интегрируя последнее равенство:
.
Интегрируя последнее равенство:
 ;
;
- Формула интегрирования по частям.
Смысл
этого правила в переходе от интегрального
выражения
![]() к выражению
к выражению
![]() ,
которое может оказаться более простым.
,
которое может оказаться более простым.
Алгоритм нахождения интеграла методом интегрирования по частям.
1.
Представить подынтегральное выражение
![]() в виде произведения
в виде произведения
![]() .
.
2.
Найти
![]() и
и
 .
.
3.
Применить формулу интегрирования по
частям .
.
4.
Найти интеграл
 .
.
5. Подставить результат в найденное в алгоритме (п. 3) выражение.
Примечание:
I.
![]() .
Следует полагать:
.
Следует полагать:
![]()
![]() Следует
полагать:
Следует
полагать:
![]()
![]() Следует
полагать:
Следует
полагать:
![]()
II.![]() Следует полагать:
Следует полагать:
![]()
![]() .Следует
полагать:
.Следует
полагать:
![]() .
.
![]() .Следует
полагать:
.Следует
полагать:
![]() .
.
(где
через
![]() обозначен многочлен).
обозначен многочлен).
Интегрирование «по частям» применяется к интегралам вида:
 ,
где
- рациональная функция,
- трансцендентная функция,
,
где
- рациональная функция,
- трансцендентная функция,
 ,
,
![]() -
рациональная функция, т.е. многочлен
любой степени.
-
рациональная функция, т.е. многочлен
любой степени.
Примеры.
1)
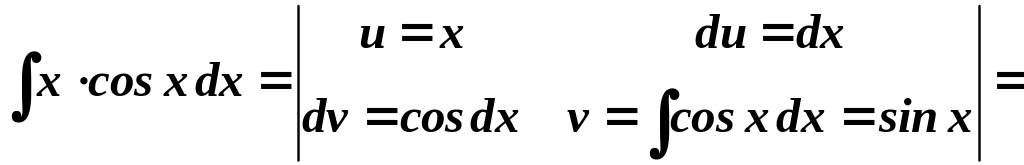

2)

4. Интегрирование выражений, содержащих квадратный трехчлен
Интегралы вида ,
после выделения полного квадрата из трехчлена, стоящего в знаменателе, приводятся к табличным интегралам:


Примеры. Вычислить

.
 .
.
II.Для нахождения интегралов вида:
 ,
,
следует
выделить в числителе дроби производную
квадратного трехчлена
![]() и разложить полученный интеграл на
сумму 2-х интегралов: первый из них имеет
табличный вид:
и разложить полученный интеграл на
сумму 2-х интегралов: первый из них имеет
табличный вид:
 ,
а второй – это интеграл вида
,
а второй – это интеграл вида
![]() или
или
![]() .
.
Примеры.
1)


 .
.
2)



 .
.
III.
Интегралы вида
 путем выделения полного квадрата
трехчлена сводятся к табличным.
путем выделения полного квадрата
трехчлена сводятся к табличным.
5. Простейшие рациональные дроби и их интегрирование
Определение:
Рациональной дробью
 называется функция, представленная
отношением двух многочленов.
называется функция, представленная
отношением двух многочленов.
Определение: Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя и неправильной в противном случае.
Примеры:
 .
.
1- правильная, 2,3 – неправильные. Любую неправильную дробь можно представить в виде суммы правильной дроби и многочлена.
Например:


Определение: Простейшими дробями называются дроби вида:
 интеграл
от дроби
интеграл
от дроби


 .
. (рассмотрено
в пункте 1.4.).
(рассмотрено
в пункте 1.4.).
Интегрирование
этой простейшей дроби производится с
помощью таких же преобразований, как в
дробях третьего вида
![]() и рекуррентной
формулы:
и рекуррентной
формулы:


Применяя
формулу
![]() раз, придем к табличному интегралу:
раз, придем к табличному интегралу:
 .
.
Пример.

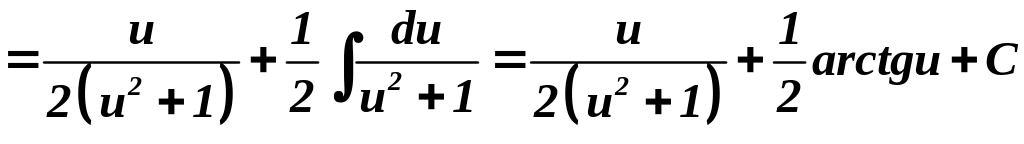 .
.
Интегрирование рациональных дробей
Пусть
![]() - многочлен
- многочлен
![]() -ой
степени, т.е.
-ой
степени, т.е.
![]()
Из алгебры известно, что многочлен имеет п корней и, следовательно, его можно разложить на множители:
![]() ,
где
,
где
![]() - корни. (1)
- корни. (1)
Например:
 .
.
Любая
правильная дробь
 может быть единственным образом
представлена в виде суммы простейших
дробей. Если знаменатель дроби разложен
на множители в виде
может быть единственным образом
представлена в виде суммы простейших
дробей. Если знаменатель дроби разложен
на множители в виде
![]() ,
то представление дроби
в виде суммы простейших дробей запишется
так:
,
то представление дроби
в виде суммы простейших дробей запишется
так:
 (2)
(2)
Линейным
множителям
 соответствуют простейшие дроби первых
двух типов, а квадратичным множителям
соответствуют простейшие дроби первых
двух типов, а квадратичным множителям
 -
простейшие дроби третьего и четвертого
вида, причем число
слагаемых,
соответствующих каждому множителю
знаменателя
равно показателю
степени
этого
множителя. Например:
-
простейшие дроби третьего и четвертого
вида, причем число
слагаемых,
соответствующих каждому множителю
знаменателя
равно показателю
степени
этого
множителя. Например:

 ;
; Коэффициенты
все неизвестны и называются неопределенными
коэффициентами. Для
их нахождения нужно привести дроби в
правой части равенства к общему
знаменателю (он будет таким же, как в
левой части) и приравнять коэффициенты
в числителях.
Коэффициенты
все неизвестны и называются неопределенными
коэффициентами. Для
их нахождения нужно привести дроби в
правой части равенства к общему
знаменателю (он будет таким же, как в
левой части) и приравнять коэффициенты
в числителях.
Получается система линейных уравнений, которая имеет единственное решение.
Пример.
Вычислить интеграл:

Разложим дробь на сумму простейших дробей:

2) Составим систему:
при


3)
 т.е. дробь разделили на разность 2-х
дробей. Следовательно, интеграл
разбивается на разность двух интегралов.
т.е. дробь разделили на разность 2-х
дробей. Следовательно, интеграл
разбивается на разность двух интегралов.

 .
.
Пример.
 .
.
Выделим целую часть, т.к. дробь неправильная, то надо разделить многочлен на многочлен.



Рассмотрим
дробь второго интеграла:
 .
.
Раскладываем на множители знаменатель:
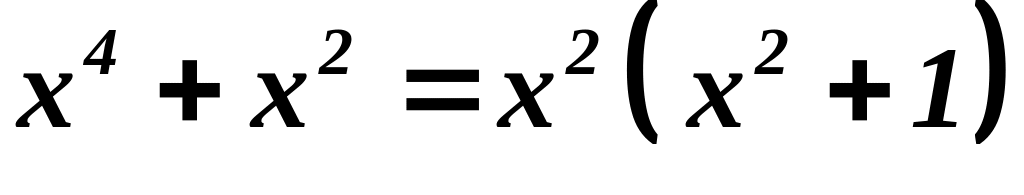 ,
,

 .
.
при






