Векторные (линейные) пространства

Категории Алгебра | Под редакцией сообщества: Математика

Векторным или линейным пространством L над полем называется непустое множество, в котором заданы операции сложения и умножения на элементы, причем выполнены следующие аксиомы:

x+y=y+x,  x+(y+z)=(x+y)+z,  α(x+y)= αx+αy,  (α+β)x= αx+ βx, (αβ)x=α(βx), 1x=x

для любых x,y,z из L и любых элементов α,β из поля. Кроме того, в L  существует нулевой элемент 0, обладающий тем  свойством, что 0+x=x для любого элемента x из L. При этом αx=0 тогда и только тогда, когда либо x=0, либо α – нулевой элемент поля.  Элементы векторного пространства называются векторами.

Базисом линейного пространства называется максимальная система независимых векторов. Независимость означает, что если сумма любой конечной подсистемы этих векторов с некоторыми коэффициентам и из поля равна нулю, то все коэффициенты равны нулю. Размерностью линейного пространства называется  число векторов в базисе. Размерность не зависит от выбора базиса.

Линейная алгебра изучает геометрические и алгебраические свойства линейных пространств над полем. В рамках линейных пространств дается  геометрическая интерпретация  решений систем алгебраических уравнений. В частности, все решения совместной системы линейных уравнений образуют плоскости и любая плоскость размерности d в n-мерном пространстве задается системой из n-d  линейных уравнений  

Если в вещественном (комплексном) пространстве выделена билинейная (полуторалинейная) функция - скалярное произведение - с определенными свойствами, то пространство называется евклидовым (эрмитовым).   Это позволяет строитьгеометрию в евклидовых и эрмитовых пространствах, определяя длины векторов, углы между ненулевыми векторами.

При изучении линейных пространств важную роль играют преобразования пространств, сохраняющие суммы векторов и умножения на элементы поля. Эти преобразования  называются линейными операторами. Ненулевой вектор x  называется  собственным с собственным значением α для оператора A, если A(x) = αx. Здесь α – элемент поля.

Симметрический оператор евклидовых и эрмитовых сохраняет скалярные произведенеия. Симметрические линейныеоператоры в квантовой механике  соответствуют физическим величинам. Значения этой величины — собственные значения оператора.

Теория симметрических операторов позволяет классифицировать поверхности второго порядка (квадрики) в евклидовных пространствах.

Координаты вектора в пространстве

Базисом в пространстве называются три некомпланарных вектора  , взятые в определённом порядке (рис.1.32). Эти векторы  называются базисными.

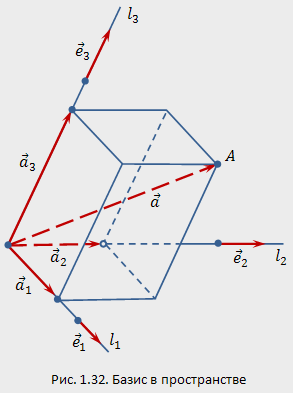
Пусть в пространстве задан базис  . Построим прямые  , содержащие базисные векторы   соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые  , параллельные прямым   соответственно, поскольку проекции вектора на параллельные прямые равны (см. свойство 1 проекций в разд. 1.2.2)). Тогда любой вектор   можно однозначно представить в виде суммы своих проекций:  , где   — векторы, принадлежащие прямым  соответственно (см. п.2 теоремы 1.1). Раскладывая проекции   по базисам на соответствующих прямых (см. разд.1.3.1), находим:  . Подставляя эти разложения в равенство  , получаем

27)

Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённойструктурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.

Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество   всех вещественных чисел с определённой на нём операцией сложения и множество   положительных вещественных чисел с заданной на нём операцией умножения. Отображение   в этом случае является изоморфизмом.