
- •Условие перпендикулярности двух векторов
- •Векторное произведение
- •Свойства [править]Геометрические свойства векторного произведения
- •[Править]Алгебраические свойства векторного произведения
- •Комплексное число
- •Определения
- •6)Решение уравнения .
- •7)Геометрическая интерпертация компл. 4исел.
- •8) Деление.
- •11) Алгоритм деления с остатком
- •12) Корни многочлена.
- •1. Сложение матриц, имеющих один и тот же размер.
- •2. Умножение матриц подходящего размера (матрицу, имеющую n строк, можно умножить справа на матрицу, имеющую n столбцов).
- •3. Умножение матрицы на элемент основного кольца или поля.
- •Теорема Лапласа
- •Векторные (линейные) пространства
- •Координаты вектора в пространстве
- •Определение линейного пространства. Изоморфизм
- •Подпространство
- •[Править]Свойства подпространств
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Матрица перехода
- •Определение
- •Характеристические корни и собственные значения
- •Собственные значения
- •Линейные преобразования с простым спектром.
- •Процесс ортогонализации Грама--Шмидта в конечномерном евклидовом пространстве
- •Уравнения прямой на плоскости
- •[Править]Общее уравнение прямой
- •12.5. Прямая линия в пространстве. Основные задачи
11) Алгоритм деления с остатком
Для любых f(x), g(x) существуют q(x) (частное) и r(x) (остаток), такие, что f(x)=g(x)q(x)+r(x), причем степень r(x) < степени g(x) или r(x) = 0. Многочлены g(x) и r(x) определены однозначно.
Частное и остаток находят с помощью так называемого правила деления "уголком".
Пример:
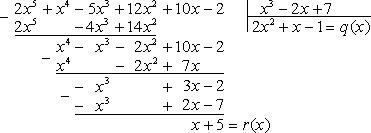
Делители многочлена.
Делитель многочлена f(x) - многочлен g(x), такой, что f(x) = g(x)q(x).
Наибольший общий делитель двух многочленов .
Наибольший общий делитель многочленов f(x) и g(x) - такой их общий делитель d(x), который делится на любой другой их общий делитель.
12) Корни многочлена.
Расмотрим многочлен :
![]() , где a1,
a2,
..., an
− целые числа, an
≠ 0.
, где a1,
a2,
..., an
− целые числа, an
≠ 0.
Если многочлен
![]() с целыми коэффициентами имеет
рациональный корень
с целыми коэффициентами имеет
рациональный корень
![]() ,
то число p является делителем числа
,
то число p является делителем числа
![]() (свободного
члена), а число q является делителем
числа
(свободного
члена), а число q является делителем
числа
![]() (старшего коэффициента).
(старшего коэффициента).
Доказательство:
Действительно, если
число
![]() является корнем многочлена
является корнем многочлена
![]() ,
то
,
то
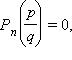 .
А именно:
.
А именно:
![]() . Умножим обе части этого уравнения
. Умножим обе части этого уравнения
на
![]() ,
получим:
,
получим:
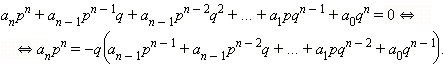 .
Так как
.
Так как
![]() - целые числа, то в скобке стоит целое
число. Значит, вся правая часть этого
равенства делится на q , так как q входит
в неё в качестве сомножителя. А значит
и левая часть тождества делится на q ,
так как она равна правой. Число p не
делится на q , так как иначе дробь
- целые числа, то в скобке стоит целое
число. Значит, вся правая часть этого
равенства делится на q , так как q входит
в неё в качестве сомножителя. А значит
и левая часть тождества делится на q ,
так как она равна правой. Число p не
делится на q , так как иначе дробь
![]() была бы сократимой, значит и
была бы сократимой, значит и
![]() не делится на q . Следовательно, на q
делится единственный из оставшихся
сомножителей левой части, а именно
не делится на q . Следовательно, на q
делится единственный из оставшихся
сомножителей левой части, а именно
![]() .
Теорема доказана!
.
Теорема доказана!
МЕТОД ГОРНЕРА.
Метод Горнера - алгоритм вычисления значения многочлена, записанного в виде суммы одночленов при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке.
Для вычисления коэффициентов частного и остатка от деления многочлена
![]() на линейный двучлен x-s очень удобно
использовать схему Горнера.
на линейный двучлен x-s очень удобно
использовать схему Горнера.
Заполняется таблица:

Полученные числа
![]() являются коэффициентами частного от
деления многочлена на двучлен, а
являются коэффициентами частного от
деления многочлена на двучлен, а
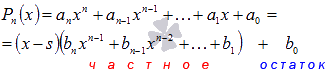
![]() - остатком. То есть,
- остатком. То есть,
Пример.
Найти частное и
остаток от деления многочлена
![]() на линейный двучлен х-1.
на линейный двучлен х-1.
Решение.
В нашем примере s =
1, коэффициенты
![]() .
.
Воспльзуемся схемой горнера:
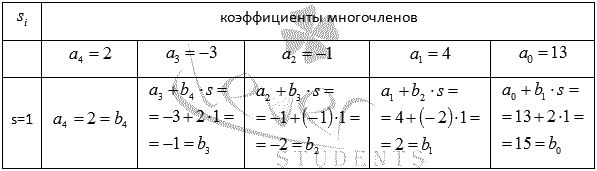
Таким образом
![]() - частное , а
- частное , а
![]() - остаток от деления.
- остаток от деления.
13)
Основна́я теоре́ма теории многочленов:
Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
СЛЕДСТВИЕ.
Немедленным следствием из теоремы является то, что любой многочлен степени n над полем комплексных чисел имеет в нём ровно n корней, с учётом кратности корней.
У многочлена f(x) есть корень a, значит, по теореме Безу, он представим в виде (x − a)g(x), где g(x) — другой многочлен. Применим теорему к g(x) и мы должны будем применять её до тех пор, пока на месте g(x) не окажется линейный множитель.
Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен x − a равен P(a).
14)
МАТРИЦЫ.ОПЕРАЦИИ НАД МАТРИЦАМИ. СВОЙСТВА ОПЕРАЦИЙ.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов целых или комплексных чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Матрицы допускают следующие алгебраические операции:
