
- •Условие перпендикулярности двух векторов
- •Векторное произведение
- •Свойства [править]Геометрические свойства векторного произведения
- •[Править]Алгебраические свойства векторного произведения
- •Комплексное число
- •Определения
- •6)Решение уравнения .
- •7)Геометрическая интерпертация компл. 4исел.
- •8) Деление.
- •11) Алгоритм деления с остатком
- •12) Корни многочлена.
- •1. Сложение матриц, имеющих один и тот же размер.
- •2. Умножение матриц подходящего размера (матрицу, имеющую n строк, можно умножить справа на матрицу, имеющую n столбцов).
- •3. Умножение матрицы на элемент основного кольца или поля.
- •Теорема Лапласа
- •Векторные (линейные) пространства
- •Координаты вектора в пространстве
- •Определение линейного пространства. Изоморфизм
- •Подпространство
- •[Править]Свойства подпространств
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Матрица перехода
- •Определение
- •Характеристические корни и собственные значения
- •Собственные значения
- •Линейные преобразования с простым спектром.
- •Процесс ортогонализации Грама--Шмидта в конечномерном евклидовом пространстве
- •Уравнения прямой на плоскости
- •[Править]Общее уравнение прямой
- •12.5. Прямая линия в пространстве. Основные задачи
12.5. Прямая линия в пространстве. Основные задачи
Угол между прямыми. Условия параллельности и перпендикулярности прямых
Пусть прямые L1 и L2 заданы уравнениями
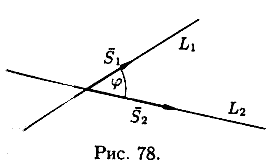
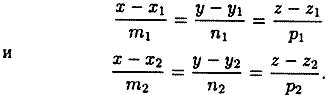
Под
углом между этими прямыми понимают угол
между направляющими векторами ![]() и
и![]() (см.
рис. 78). Поэтому, по известной формуле
для косинуса угла между векторами,
получаем
(см.
рис. 78). Поэтому, по известной формуле
для косинуса угла между векторами,
получаем
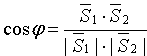 или
или
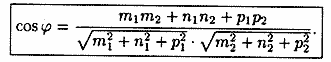 (12.16)
(12.16)
Для нахождения острого угла между прямыми L1 и L2 числитель правой части формулы (12.16) следует взять по модулю.
Если
прямые L1 и
L2 перпендикулярны,
то в этом и только в этом случае имеем
cosСледовательно,
числитель дроби (12.16) равен нулю, т. е. ![]()
Если
прямые L1 и
L2 параллельны,
то параллельны их направляющие
векторы ![]() и
и ![]() .
Следовательно, координаты этих векторов
пропорциональны, т. е.
.
Следовательно, координаты этих векторов
пропорциональны, т. е. ![]() .
.
Условие, при котором две прямые лежат в одной плоскости
Пусть прямые L1 и L2 заданы каноническими уравнениями
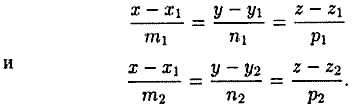
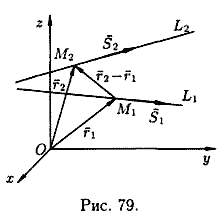
Их направляющие векторы соответственно и (см. рис. 79).
Прямая
L1 проходит
через точку ![]() радиус-вектор
которой обозначим через
радиус-вектор
которой обозначим через ![]() ;
прямая L2 проходит
через точку
;
прямая L2 проходит
через точку ![]() ,
радиус-вектор которой обозначим через
,
радиус-вектор которой обозначим через ![]() .
Тогда
.
Тогда
![]()
Прямые
L1 и
L2 лежат
в одной плоскости, если
векторы
,
и ![]() компланарны.
Условием компланарности векторов
являтся равенство нулю их смешанного
произведения:
компланарны.
Условием компланарности векторов
являтся равенство нулю их смешанного
произведения: ![]() ,
т. е.
,
т. е.
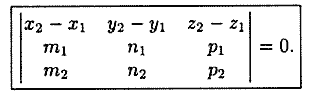
При
выполнении этого условия прямые L1 и
L2 лежат
в одной плоскости, то есть либо
пересекаются, если ![]() ,
либо параллельны, если
,
либо параллельны, если ![]() .
.
45)
Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
![]()
или
![]()
пересекаются в точке
![]()
Угол γ12 между пересекающимися прямыми определяется формулой
![]()
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрами A1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти
прямые параллельны,
если A1B2 − A2B1 =
0 или k1 = k2,
и перпендикулярны,
если A1A2 + B1B2 =
0 или ![]() .
.
Любую прямую, параллельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
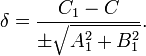
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
![]()
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие

Если ![]() и
и ![]() ,
то прямые
,
то прямые ![]() и
и ![]() перпендикулярны.
перпендикулярны.
