Уравнения прямой на плоскости

Способы задания прямой:  или  .

[Править]Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B)называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

[править]Уравнение прямой с угловым коэффициентом

Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке   и образующая угол   с положительным направлением оси Ox:

Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

[править]Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке   и ось Oy в точке  :

В этом виде невозможно представить прямую, проходящую через начало координат.

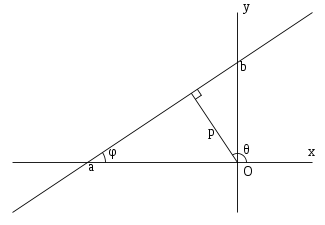
[править]Нормальное уравнение прямой

где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол   задаёт угол наклона прямой.

41)

Нормальное уравнение прямой

где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол   задаёт угол наклона прямой.

Вывод нормального уравнения прямой  [показать]

Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cos θ и sin θ выражаются через коэффициенты A, B и C следующим образом:

Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cos θ и sin θ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного направления произволен.

Нормальное уравнение прямой. Расстояние от данной точки до данной прямой

1. Нормальное уравнение прямой

где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а   - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель  , взятый со знаком, противоположным знаку свободного члена C.

2. Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

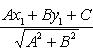
Правило. Чтобы определить расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:

Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.

Отклонение   данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.

42)

m-плоскость в пространстве Rⁿ

Пусть дано n-мерное аффинный-точененое пространство Kⁿ(V,P), над полем действительных чисел. В нём выбрана прямоугольная система координат  . m-плоскостьюназывается множество точек α, радиус векторы которых удовлетворяют следующему соотношению   A_nm - матрица, столбцы которой образует направляющие подпространство плоскости,   - вектор переменных,   - радиус-вектор одной из точек плоскости. Указанное соотношение можно из матрично-векторного вида перевести в векторный:  - векторное уравнение m-плоскости. Вектора   образуют направляющее подпространство. Две m-плоскости α,β называются параллельными, если их направляющие пространства совпадают и  .

(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть   - нормальный вектор плоскости,   - вектор переменных,   - радиус вектор точки, принадлежащей плоскости, тогда:  - общее уравнение плоскости. Имя матрицу направляющих векторов, уравнение можно записать так:  , или: 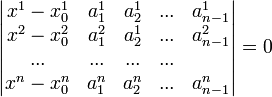. Углом между плоскостями называется наименьший угол между их нормальными векторами.

Уравнения плоскости

Впервые встречается у А. К. Клеро (1731).

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).

Нормальное уравнение ввёл Л. О. Гессе (1861).

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

• Общее уравнение (полное) плоскости

где   и   — постоянные, причём   и   одновременно не равны нулю; в векторной форме:

где   — радиус-вектор точки  , вектор   перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора  :

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При   плоскость проходит через начало координат, при   (или  ,  ) П. параллельна оси   (соответственно   или  ). При   ( , или  ) плоскость параллельна плоскости   (соответственно  или  ).

• Уравнение плоскости в отрезках:

где  ,  ,   — отрезки, отсекаемые плоскостью на осях   и  .

• Уравнение плоскости, проходящей через точку 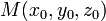  перпендикулярно вектору нормали  :

в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки 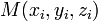 , не лежащие на одной прямой:

(смешанное произведение векторов), иначе

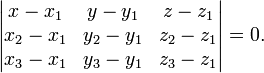
• Нормальное (нормированное) уравнение плоскости

в векторной форме:

где  - единичный вектор,   — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

(знаки   и   противоположны).

43)

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора  , имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

П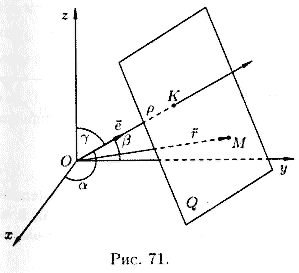 усть ОК = p, а α, β,  — углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор  . При любом положении точки Μ на плоскости Q проекция радиус-вектора   на направление вектора   всегда равно р:  , т. е.   или

     (12.8)

Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e, уравнение (12.8) перепишем в виде

        (12.9)

Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на норми­рующий множитель  , где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

Расстояние от точки до плоскости

Пусть задана точка   и плоскость Q своим уравнением  . Расстояние d от точки   до плоскости Q находится по формуле

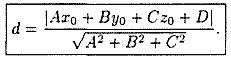
Вывод этой формулы такой же, как вывод формулы расстояния от точки   до прямой .

Расстояние d от точки M₀ до плоскости Q равно модулю проекции вектора  , где   — произвольная точка плоскости Q, на н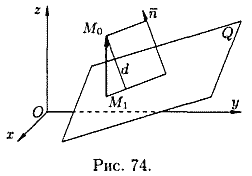 аправление нормального вектора   (см. рис. 74). Следовательно,

 

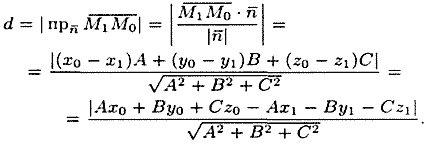
А так как точка   принадлежит плоскости Q, то

Поэтому 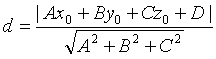 . Отметим, что если плоскость Q задана уравнением  , то расстояние от точки   до плоскости Q может быть найдено по формуле

  

44)