3.7 Свойства определителя
Каждое слагаемое в сумме (3.18) имеет вид
(3.21)
и называется членом
определителя
-го
порядка. Член определителя является
произведением
элементов, взятых точно по одному из
каждой строки и каждого столбца
определителя, и числа
.
Действительно, присутствие в произведении
(3.21) по одному элементу из каждой строки
является очевидным. Кроме того, из
определения перестановки
-ой
степени ясно, что
,
и следовательно, в произведении (3.21)
присутствует точно по одному элементу
из каждого столбца определителя. Верно
и обратное, любое произведение из
элементов определителя
,
,
(3.22)
взятых точно по одному из каждой его строки и каждого столбца, входит в сумму (3.18) либо со своим, либо с противоположным знаком. Перестановка , порождающая соответствующий член определителя, имеет вид
.
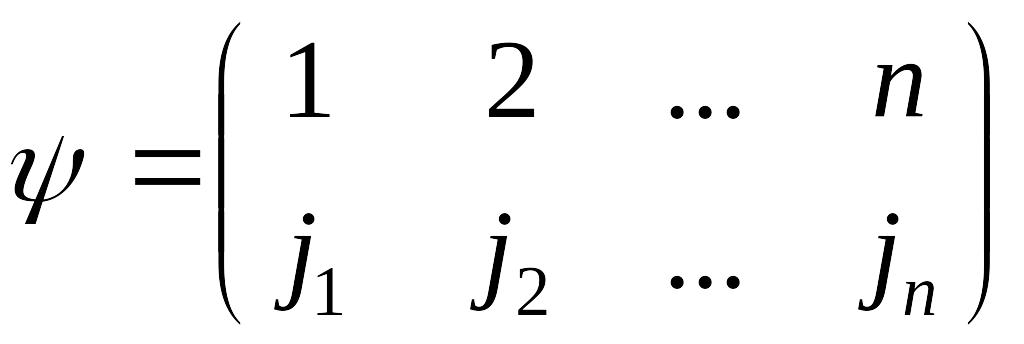(3.23)
Если
– четная перестановка, то произведение
(3.22) входит в сумму (3.18) со своим знаком,
а если
– нечетная перестановка, то – с
противоположным знаком. В связи с этим
основному определению предыдущего
пункта можно придать другую эквивалентную
ему форму: определителем матрицы
,
,
называется сумма всевозможных произведений
(число этих произведений равно
)
по
элементов этой матрицы, взятых по одному
из каждой её строки и каждого её столбца,
причем каждое произведение входит в
указанную сумму со своим знаком, если
порождаемая нумерацией его элементов
перестановка (3.23) четная, и – с
противоположным знаком, если эта
перестановка нечетная.
Рассмотрим основные свойства определителя. Всюду ниже будем предполагать, не подчеркивая этого всякий раз, что матрица .
Предложение 3.6
.
◄ Первое
доказательство.
Введем обозначение
Ясно, что
,
.
По определению
. (3.24)
Покажем, что эта сумма совпадает с суммой (3.18). Действительно, каждое произведение
(3.25)
является членом определителя , так как содержит точно по одному элементу из каждого столбца и каждой его строки ( – перестановка -ой степени). Именно,
,
где
.
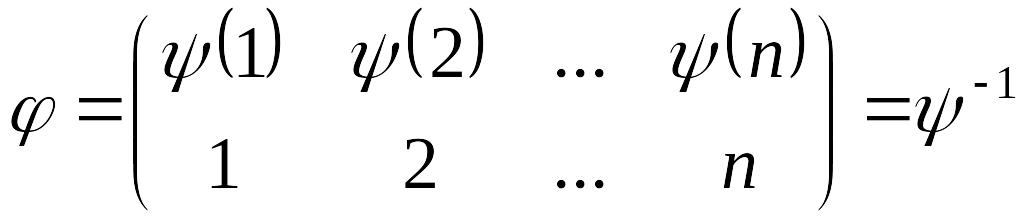Одновременно,
,
так как разложив перестановку
в произведение транспозиций произвольным
образом
,
замечаем, что
,
т.е. перестановки
и
одновременно четные или нечетные.
Поскольку различные слагаемые суммы
(3.24) совпадают с различными членами
определителя
,
ясно, что
Второе доказательство. Сумму (3.24) запишем в виде
и в соответствии
с принципом замены переменного индекса
проведем две замены: вначале в произведении,
а потом в сумме. Зафиксируем перестановку
.
Так как
является перестановкой элементов
множества
и
,
то в соответствии с пунктом 3.5 замена
приводит к равенству
,
т.е.
(3.26)
Отображение
является перестановкой элементов
множества
,
так как оно обратимо,
.
Проводя в сумме
(3.26) замену
и учитывая, что
,
получаем, что
.
►
Из только что доказанного свойства следует, что строки и столбцы определителя равноправны в том смысле, что любое свойство его строк верно также и для его столбцов и наоборот, любое свойство столбцов определителя выполняется также для его строк. С учетом этого замечания последующие свойства определителя будем формулировать, в основном, в терминах его строк.
Предложение 3.7.
Если матрица
получена из матрицы
элементарным преобразованием
,
тогда
.
Иными словами, при перемене местами двух строк определителя он меняет знак на противоположный.
◄ В матрице
,
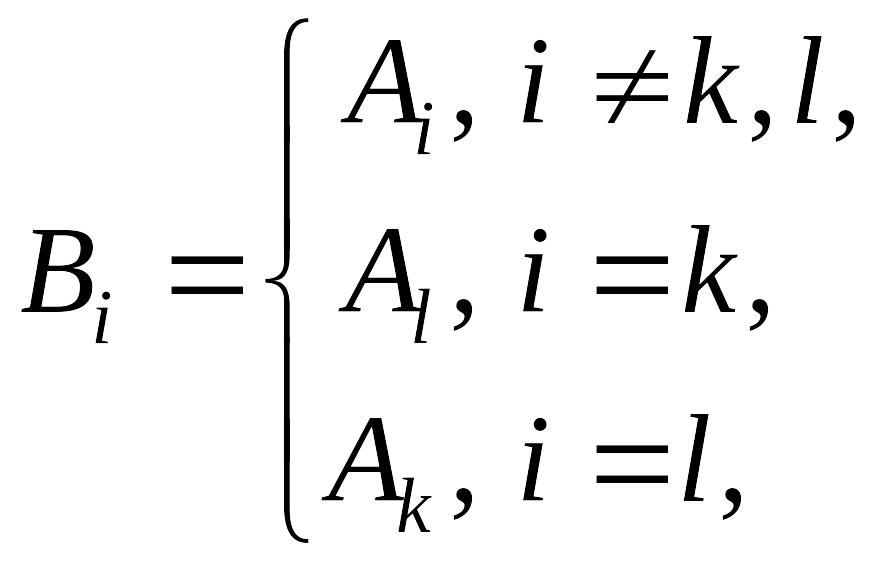т.е.
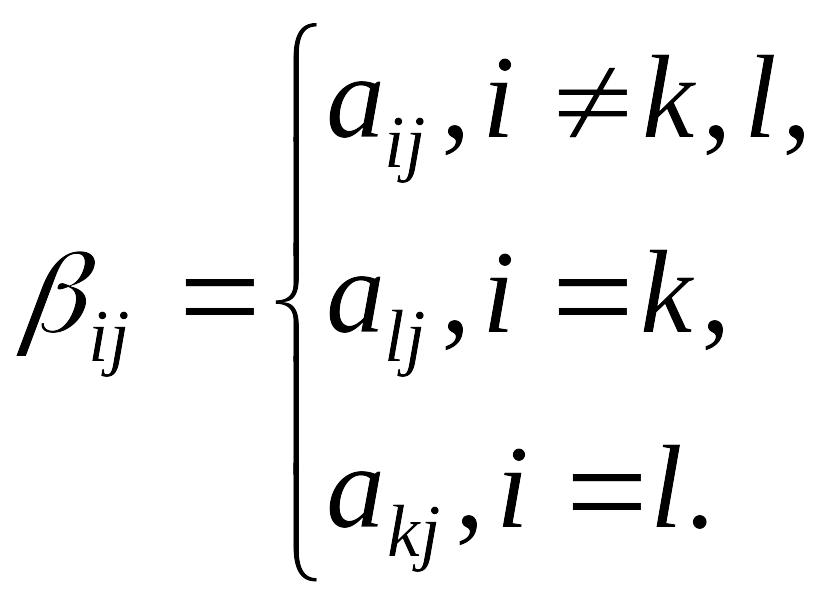
Поэтому, считая
для определенности
,
получаем, что
.
(3.27)
Рассмотрим следующую
перестановку f
элементов
множества
,
,
где t
–транспозиция. Действительно, отображение
обладает свойством
и поэтому обратимо,
.
Вводя обозначение
,
замечаем, что
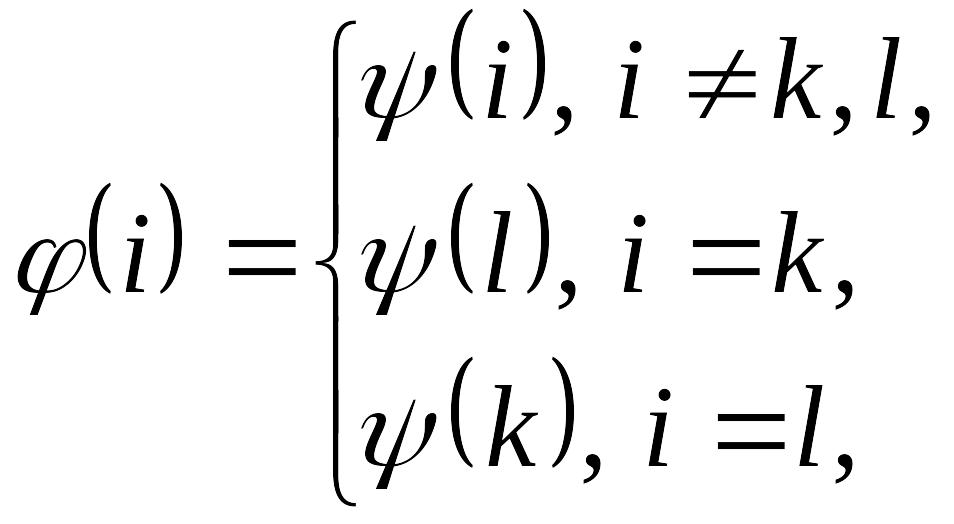
и
,
так как перестановки
и
имеют различную четность. Учитывая это
и проводя замену переменной
в сумме (3.27), получаем, что
.
►
В качестве иллюстрации замечания о равноправии строк и столбцов определителя покажем, что при перемене местами двух столбцов определитель меняет знак на противоположный.
◄ Пусть матрица
получена из матрицы
элементарным преобразованием
.
Тогда матрица
получается из матрицы
элементарным преобразованием
,
и по доказанному
.
Откуда, используя предложение 3.6,
получаем, что
.►
Предложение 3.8.
Если матрица
получена из матрицы
элементарным
преобразованием
,
тогда
.
◄ В матрице
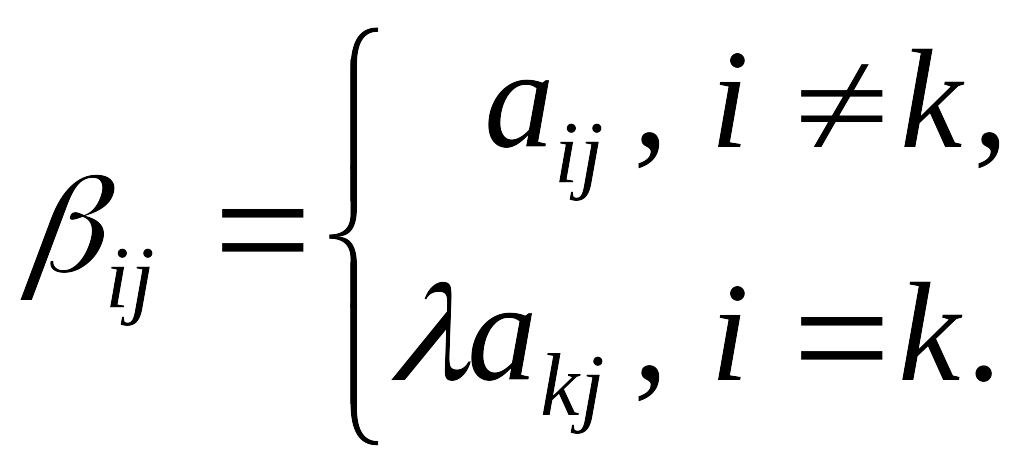
Поэтому
.
►
В качестве следствия этого свойства получаем, что
. 
Из предложения 3.8 вытекает также следующее правило выноса числового множителя за знак определителя,
,
где
получается из матрицы
делением всех элементов какой-нибудь
её строки или какого-нибудь её столбца
на
.
Например,
.
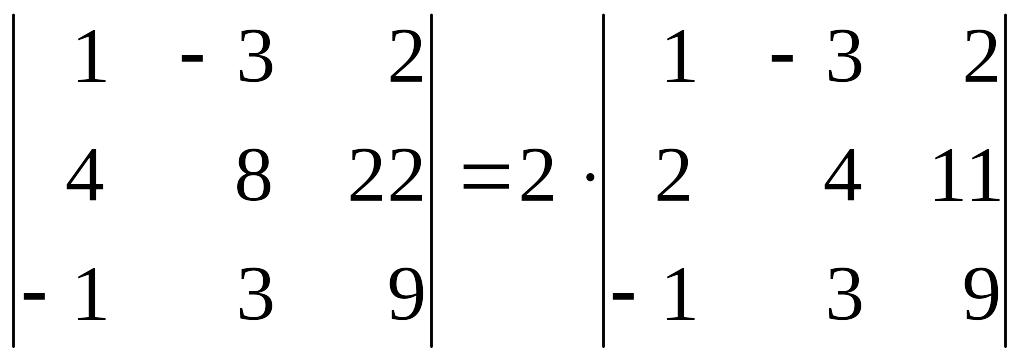Здесь проведен вынос числа 2 за знак определителя из второй строки.
Предложение 3.9. Если матрица содержит нулевую строку, её определитель равен нулю.
Предложение 3.10. Если матрица содержит две пропорциональные строки, её определитель равен нулю.
◄ Пусть
.
Можно считать, что
,
так как случай
содержится в предложении 3.9. Если
,
т.е.
,
в матрице
проводим элементарное преобразование
.
При этом в силу предложения 3.7 определитель
меняет знак. В то же время матрица
,
а с нею и
не изменились, т.е.
.
Если
,
в матрице
проводим элементарное преобразование
.
После этого получаем матрицу
с равными строками,
.
В силу предложения 3.8 с учетом предыдущего
случая
.
►
Предложение
3.11. Если
строка
матрицы
представима в виде суммы двух векторов-строк
порядка
,
,
её определитель
,
где матрица
получается из матрицы
заменой
,
а матрица
– заменой
.
◄ Пусть
.
Тогда
.
►
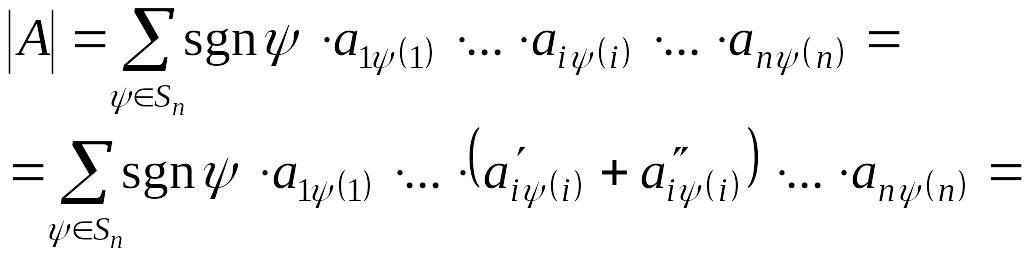
Предложение
3.12. Если
матрица
получена из матрицы
с помощью элементарного преобразования
,
,
тогда
.
◄ В матрице
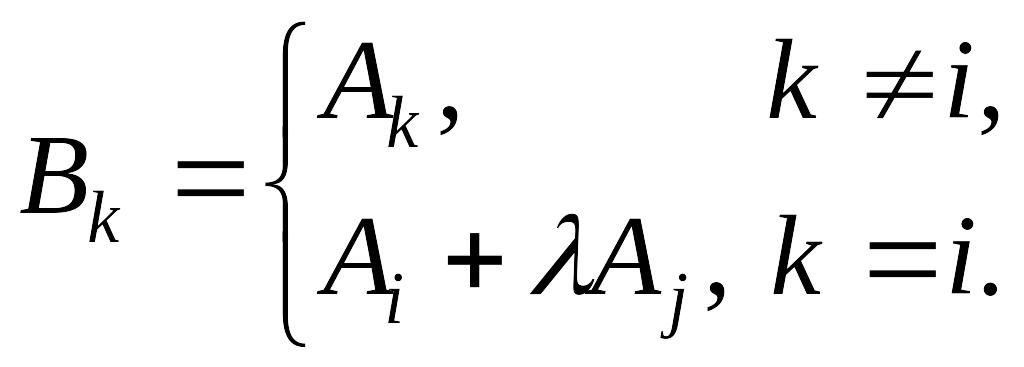
Выделяя в определителе
строки
и
,
учитывая при этом, что остальные строки
совпадают с соответствующими строками
определителя
,
в силу предложения 3.11 имеем
,
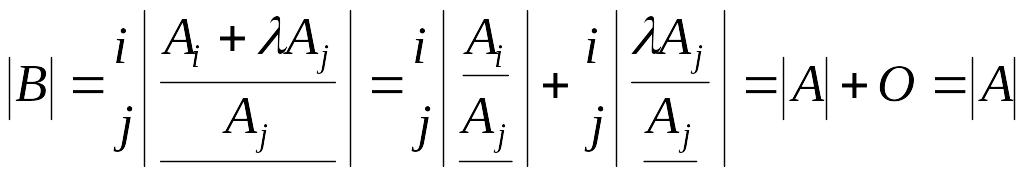так как второй определитель имеет пропорциональные строки и, следовательно, равен нулю. ►
Предложение 3.13 Определитель матрицы верхнетреугольного или нижнетреугольного вида равен произведению его диагональных элементов.
◄ Пусть, например,
.
Очевидно, что все
члены этого определителя, не содержащие
в качестве элемента первой строки, равны
нулю. Из второй строки к этому элементу
можно добавить лишь
,
так как
брать нельзя, поскольку первый столбец
уже занят, а все остальные элементы
второй строки равны нулю. Продолжая
аналогичные рассуждения для последующих
строк, получаем, что единственно возможным
ненулевым членом определителя остается
произведение
,
порождаемее перестановкой
,
т.е.
.
►
Предложение 3.14. Любую матрицу можно привести к верхнетреугольному или нижнетреугольному виду только строчными (только столбцовыми) элементарными преобразованиями, не меняя её определителя.
◄ Рассмотрим
случай верхнетреугольной матрицы и
строчных элементарных преобразований.
Если
,
тогда первый столбец матрицы
уже имеет нужный вид, и можно переходить
ко второму столбцу. Если
,
но
,
существует ненулевой элемент
.
Совершая вспомогательное преобразование
,
добиваемся выполнения условия
.
Пусть . В матрице проводим следующую цепочку элементарных преобразований,
.
В силу предложения 3.12 получаем, что
.
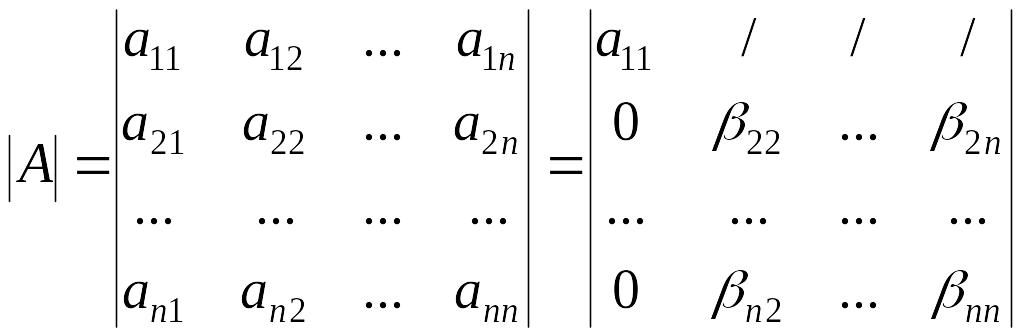Если все элементы
второго столбца последнего определителя,
начиная со второго, равны нулю, переходим
к его третьему столбцу. В противном
случае, строчными элементарными
преобразованиями, не меняя определителя,
добиваемся выполнения условия
.
Проводя цепочку элементарных преобразований
,
приходим к определителю
.
Ясно, что продолжая этот процесс, на -ом шаге мы получим матрицу верхнетреугольного вида, определитель которой равен определителю ,
.
Для того, чтобы
матрицу
строчными элементарными преобразованиями
привести к нижнее треугольному виду,
не меняя её определителя, нужно с помощью
элемента
получить нули в последнем столбце и
т.д. Случай столбцовых преобразований
рассматривается аналогично. ►
Лекция XI.
План
3.8 . Теорема Лапласа.
3.9. Разложение определителя по элементам строки или столбца.