Запитання і завдання до теми:

1. Назвіть основні геометричні поняття і уявлення початкового курсу математики

2. З метою узагальнення поняття і уявлення про різні плоскі геометричні фігури вчитель використав гру "Назви ім'я". Які наочні посібники доцільно використовувати для цього? Які інші ігри можна використати з цією ж метою?

3. Яким чином і в якій послідовності формуються поняття о геометричних фігурах?

4. Розв'яжіть задачі геометричного змісту (Богданович М.В. Математика 4(3) .№ 679, 680, 684 ст. 123, 124). Поясніть методику роботи над задачами.

5. На що повинен звернути увагу вчитель при розв’язуванні задачі: “Поділити прямокутник на дві рівні частини так, щоб кожна з них була: 1. Прямокутником; 2. Трикутником; 3. Чотирикутником?”

6. На що повинен звернути увагу вчитель при розв’язуванні задачі: “Поділити прямокутник на дві рівні частини так, щоб кожна з них була: 1) прямокутником; 2) трикутником; 3) чотирикутником”?

7. Перетворіть задачу: “Побудуйте два різні прямокутники, але такі, щоб площа кожного дорівнювала 12 см²” – на таку, щоб площа двох прямокутників дорівнювала б 12 см².

8. Зі скількох простих задач геометричного змісту складається задача: “Скільки на малюнку (мал.1) всього чотирикутників? Трикутників? Виміряй довжину відрізка, який є периметр чотирикутника АВСД?” Які вимірювально-креслярські інструменти повинен використати учень при виконанні цього завдання?

В С

А К D

Мал. 1.

9. Розглянути публікації з журналів та газети “Початкова школа”, “Начальная школа”, “Розкажи онуку”, “Освіта” (висвітлення актуальних проблем заданої теми). Форма роботи – обговорення повідомлень.

Тема № 14.

Тема: Методика роботи над дробами.

Мета вивчення: навчити студентів володіти методикою ознайомлення з частинами величини та дробами, розв'язувати відповідні задачі.

Література: І.З.Василенко. Методика викладання математики в початкових класах. - К., Вища шк. 1971. Розділ 13.

Богданович М.В. Методика викладання математики в початкових класах. - К., "АЕК", 1999. (Розділ 12).

Друзь Б.Г. Творчі вправи з математики для початкових класів. - К, 1988.

План

1. Методика ознайомлення учнів з частинами і з дробами.

2. Методика розв’язування задач на знаходження частини від числа і числа за однією частиною.

1. Ознайомлення учнів з «частинами» має своїм завданням створити у дітей конкретні уявлення про процес утворення частин від цілого предмета або однієї одиниці, чи певної сукупності предметів. Для практичних робіт на уроках ручної праці, для засвоєння нотної грамоти на уроках співів у початкових класах треба знати найпростіші дроби (половина, чверть та ін.). Крім того, ознайомлення учнів початкових класів з «частинами» полегшує вивчення дробів у наступних класах середньої школи.

За новою програмою в 3 класі учні повинні ознайомитися з утворенням частин одиниці, їх порівнянням; навчитися записувати і читати найпростіші дроби із знаменником до 10, знаходити одну частину від числа та числа за даною його частиною. У 4 класі учні вчаться перетворювати дроби із знаменниками в межах 10 та знаходити кілька частин від числа.

Розглядають ці питання з допомогою наочності, використовуючи велику кількість практичних вправ, пов’язаних з кресленням, вирізуванням, вимірюванням, перегинанням, практичним поділом круга, прямокутника, відрізків на 2, 4, 8, 3, 6, 9 рівних частин. Тому слід забезпечити кожного учня необхідним для використання пізнавальних завдань: циркулем, лінійкою, кольоровим олівцем, ножицями і папером для вирізування кружечків і смужок.

Дидактичний матеріал учні виготовляють на уроках ручної праці: по 4 кружечки діаметром 5-8 см, по одному квадрату з стороною 5 см, прямокутнику з сторонами 5 см і 8 см, п’ять смужок паперу 2-4 см завширшки і 10-20 см завдовжки. Для конкретизації поняття про долі доцільно також використовувати круглі овочі і фрукти (яблука, картоплю тощо), а для фронтального показу чотири круги з тонкого картону діаметром 10-15 см, поділених на сектори і пофарбованих у різні кольори та з відповідними записами на кожному (1/2, 1/4 1/8, 1/10, 1/3, 1/6, 1/9).

Ознайомлення з частинами. Утворення частин. Вивчати поняття про частини слід у такій послідовності: а) формування в учнів поняття про половину, чверть і т.д. (утворення частин діленням на рівні частини кружечка, яблука, смужки паперу, тощо); б) лічба частинами одиниці; в) записування дробу; г) читання дробу; д) порівняння кількох однойменних (дробів з однаковими знаменниками) і різнойменних (дробів з різними знаменниками) частин. При першому ознайомленні з частинами доцільно використовувати таку наочність, щоб частина не тільки за величиною, а й за формою відрізнялася від цілого.

Покажемо, для прикладу, як сформувати в дітей чіткі уявлення про половину та ознайомити їх із записом відповідного дробу. Вчитель ставить завдання показати половину кружечка, половину смужки паперу,мити їх із записом відповідного дробу. а й за формою запитує, хто бачив половину кавуна, хліба тощо. Перегинаючи смужку паперу чи кружечок навпіл, діти роблять висновок, що половини одного й того ж кружечка чи тієї самої смужки паперу рівні.

Вчитель показує демонстраційний картонний круг, згинає його навпіл, пропонує дітям вирізаний дома кружечок розрізати так само і наклеїти в зошити, залишивши вузький проміжок між по­ловинами кружечка, зафарбувати їх кольоровим олівцем тощо. Як називається наклеєна частина круга? (Половина, або одна друга).

Порівнюємо накладанням половини круга (вони рівні між собою). Як порівняти між собою наклеєні половини круга? Які вони будуть між собою?

Мама дала завдання: поділити одно яблуко порівну між двома сестричками. Як виконаєте завдання? (Розріжемо яблуко на дві рівні частини). Один учень розрізує, а решта спостерігають, чи правильно він виконує завдання. Як називається одна частина яблука? (Половина, або одна друга). Які по величині половини одно­го яблука? Скільки половин у одному яблуці? А що більше: по­ловина цього яблука чи ціле яблуко? Що менше: половина вашого кружечка чи цілий кружечок, який ви розрізали навпіл?

За пропозицією вчителя два учні перегинають, а потім розрі­зують половини демонстраційного круга навпіл. На скільки всього частин розрізали круг? Порівняйте, які вони по. величині між со­бою? Як будемо називати одну таку частину цілого круга? (Одна четверта, або чверть). А скільки четвертих частин в одному ціло­му крузі? А чому ми назвали одну частину круга четвертою части­ною? Візьміть свій другий цілий круг і спочатку поясніть, як перегинанням круга можна знайти одну восьму його частину. Зро­біть і покажіть одну восьму частину круга. Які за величиною між собою восьмі частини одного круга? Що менше: одна восьма чи одна четверта круга? Як можна назвати кожну частину круга, якщо його поділимо: на 4 рівні частини? на 8 рівних частин? на 6 рівних частин? на 10 рівних частин?

Наше завдання довести на цьому уроці до свідомості дітей зв'язок між назвами частин і тим, на скільки рівних частин поділили ціле (якщо ціле поділили на 2 рівні частини, то кожна така частина— одна друга, якщо на чотири,— одна четверта і т. д.).

Потім учні знаходять половину накресленого на дошці і виміряного відрізка. Креслять у зошитах квадрат із стороною, наприклад, 4 см. Ділять його на 4 рівні частини так, щоб було 4 квадрати. Зафарбовують червоним олівцем четверту частину великого квадрата і ділять її навпіл. Відповідають на запитання вчителя: які фігури утворилися? Скільки таких фігур у всьому великому квадраті?

На другому уроці учні ознайомлюються з записом та порівнянням частин. Учні креслять у своїх зошитах 3 однакових круги (радіус 2 см), а на дошці 3 круги (радіус 2 дм). Учитель ділить круги на дошці, а учні - в зошитах за вказівками вчителя: перший круг навпіл, другий на 4, а третій на 8 рівних частин. Повторюють, на скільки рівних частин поділено перший круг, як називаються частини першого круга. Учитель пояснює, як запитується і записує на кожній половині першого круга . Учні записують на кожній половині свого першого круга в зоши­тах . У другому крузі записують на кожній четвертій частині у третьому

Учитель показує, як треба посередині між двома клітинками провести спочатку горизонтальну риску, у верхній клітинці над рискою написати цифру 1, а в нижній — під рискою цифру 2 (у другому крузі 4, у третьому 8). Число, записане під рискою, показує, на скільки рівних частин поділено ціле, а число 1, напи­сане над рискою, показує, що взяли таку одну частину.

Після усвідомлення поняття про частину одиниці, учні лічать частинами одиниці. Використовуючи дидактичний матеріал, вони лічать: перша, друга половина (кружечка); перша, друга, третя третина (смужки паперу) і т.п. У процесі такої лічби учні з'ясо­вують, що цілу одиницю (кружечок, смужку паперу тощо) можна представити двома половинами, трьома третіми частинами, чотир­ма четвертими і т. д.

У III класі вчитель показує, як записати і щоразу вимагає взяти відповідну частину кружечка чи смужки паперу. Поділивши перегинанням один кружечок на 4, другий такий самий на 8 рівних частин тощо, діти наклеюють на аркушах зошита чверть, одну восьму частину такого кружечка.

Аналогічно, накресливши відрізок в 12 клітинок завдовжки, вони відокремлюють дужкою цього відрізка. Достатня кількість розв'язання таких вправ сприятиме формуванню чітких .уявлень в учнів про дробове число.

Терміни чисельник і знаменник не слід подавати і учням на перших порах, а тільки, згодом, коли вони добре усвідомлять функцію знаменника і чисельника в позначенні дробу.

Разом з записом частин порівнюють різні частини від одного кружечка, від однієї одиниці. Спочатку порівнюють практично, на основі накладання або зорового зіставлення, використовуючи для цього заготовлені кружечки, смужки паперу, накреслені відрізки, прямокутні фігур.

Для чіткого усвідомлення величини частин від однієї одиниці вчитель пропонує поділити перегинанням цілий кружечок на дві рівні частини, порівняти ці частини (вони рівні): порівняти половину кружечка з цілим (половина менша від цілого); порівняти четверті частини від такого ж самого кружечка (вони всі рівні); порівняти четверту частину з цілим кружечком (вона менша); по­рівняти четверту частину кружечка з його половиною і т.д. Доцільно в зошитах наклеїти зафарбований кружечок, а поруч з ним одержані від такого самого кружечка зафарбовані частини: а в другому рядку:

Діти повинні зрозуміти, що коли ціле поділити на рівні частини, то кожна частина буде менша від цього цілого; чим на більшу кількість частин поділено ціле, тим кожна частина його буде менша.

На підставі цього учні повинні дати відповідь на запитання:

«Що більше: чи того самого цілого? чи одного цілого, пояснити чому більша , чому більша , чому більша ?»

Результати порівняння слід записувати, використовуючи зна­ки >, <.

Після цього можна розпочати ознайомлення учнів із знахо­дженням частини числа. За пропозицією вчителя учні кладуть пе­ред собою певну кількість кружечків, ділять їх на дві рівні частини і показують половину кружечків. Як узнати, скільки кружечків становлять всіх цих кружечків? Ділять смужку паперу, відрі­зок прямої певної довжини на 2, 3, 4 рівні частини, показують половину, третину, чверть смужки паперу, відрізка. Як узнати, чому дорівнює половина смужки паперу? третя частина?

Лише після розв'язання таких вправ можна перейти до роз­в'язування життєвих задач на знаходження однієї частини, а в ІІІ класі - кількох частин числа.

2. Задачі на знаходження однієї або кількох частин числа.

1. Неодмінною умовою успішного навчання учнів розв'язувати задачі на знаходження спочатку однієї, а пізніше й кількох частин числа є усвідомлення ними за допомогою дидактичного матеріалу і фронтальних наочних посібників поняття про частини та їх утворення.

Перед розв'язуванням таких задач треба Допомогти дітям зро­бити деякі умовиводи про співвідношення між цілою одиницею і частинами її, а саме: третя (восьма, п'ята) частина круга (смужки паперу) в три рази (вісім, п’ять) менша, ніж цілий круг (вся смужка); більше, ніж круга в 3 рази; шляху, пройденого ман­дрівником, у 8 раз коротша, ніж весь шлях і т. п.

Після цього слід перейти до розв'язування задач на знахо­дження однієї частини числа, наприклад:

«Від 12 м дроту відрізали третю частину. Скільки метрів дроту відрізали?»

Учні розв'язують задачу міркуючи так: щоб знайти третю час­тину від 12 м, треба поділити 12 м на 3. Записують розв'язування і відповідь у рядок.

Розв’язання. 12 м : 3 = 4 м. В і д п о в і д ь: від 12 м дорівнює 4 м.

Аналогічні міркування і записи застосовують і при розв'язу­ванні наступних задач, у яких треба знайти четверту частину метра (100 см : 4) четверту частину

центнера (100 кг : 4), півтонни (1000 кг : 2) тощо. A B C Q

Рис. 1

Корисно давати дітям і завдання графічного характеру, Наприклад:

накреслити відрізок прямої АД = 12 см, поділити його на 3 рівні частини, позначивши точки поділу буквами В і С (рис. 1). Скільком сантиметрам дорівнює відрізок АД? відрізок АС?

Пізніше розв'язують і вправи на знаходження однієї частини від абстрактних чисел, наприклад:

від 90; від 28; від 16, 32, 36 і т.д.

Розв'язання. 90 : 5 = 18 і т. д.

Приступаючи в III класі до розв'язування задач на знаходження кількох частин числа, слід провести такі практичні за­вдання:

1.Обкреслити смужку в 16 кліток завдовжки. смужки пофар­бувати в червоний колір, другу чверть - у синій, третю чверть - у жовтий. Скільки всього кліток пофарбовано? Яка частина всієї смужки пофарбована?

2. Обкреслити смужку в 16 клітинок завдовжки.

Пофарбувати смужки в синій колір. У скільки разів більше синіх клітинок, ніж білих (не пофарбованих)?

2. Приготувати три паперові смужки кожна по 40 см завдовжки. Зафарбувати довжини першої смужки, другої і 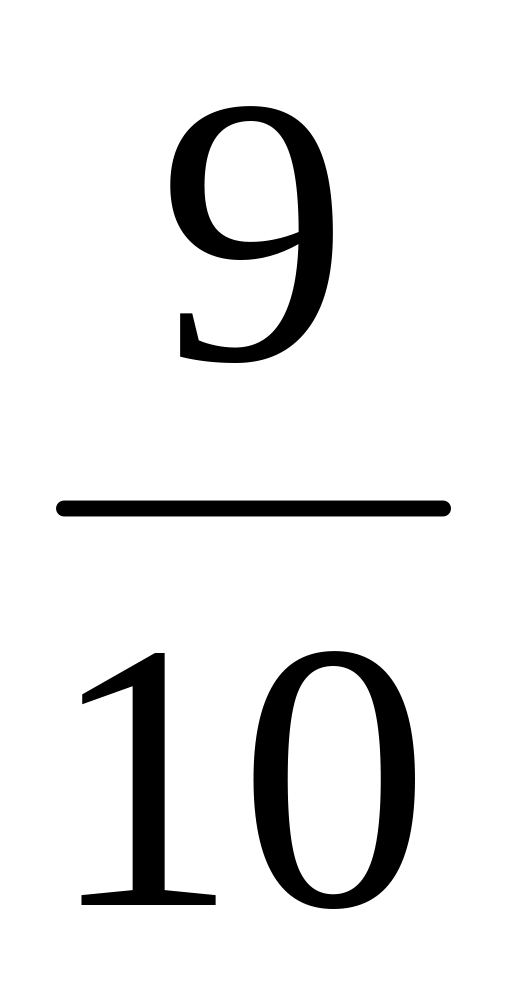третьої. Скільки сантиметрів кожної смужки зафарбовано?

Після усного розв'язування цієї вправи вчитель показує, як записати обчислення:

від 40 см = ?

1. 40 см : 4 = 10 см;

2. 10 см · 3 = 30 см.

Відповідь: від 40 см дорівнює 30 см.

За таким зразком записують розв'язування вправ з другою і третьою смужками.

Потім учитель підводить учнів ІІІ класу до такого, висновку: щоб знайти від числа (40 см), треба спочатку знайти одну (чет­верту) частину його і одержану част­ку (10 см) помножити на 3.

10 cм

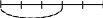
С

А В А В

Рис. 2

На наступних уроках учитель переходить до розв'язування склад­ніших задач, наприклад:

Учні принесли з лісу для посадки саджанці — ялинки і берізки. Яли­нок було 40, а число берізок становило від числа ялинок. Скільки берізок принесли учні?

Розв'язання:

1. 40 : 8 = 5;

2. 5 · 5 =25.

В і д п о в і д ь. 25 берізок.

Поряд з розв'язуванням таких задач треба давати учням за­вдання знаходити кілька частин від абстрактних чисел:

Знайти від кожного з таких чисел: 72, 360, 280, 732.

Знайти від числа 60 і т. п.

Практичне завдання. Накресліть відрізок завдовжки 10 см. Скільки сантиметрів у цього відрізка? (Рис. 2).

Знайдемо спочатку, скільки сантиметрів у цього відрізка:

10 : 5 = 2 (см)

Знайдемо, скільки сантиметрів у відрізка:

2 · 3 = 6 (см)

Запишемо коротше: 10 : 5 · 3 = 6 (см).

2. Задачі на знаходження числа за однією його частиною (3-4 клас)

Як знаходити число за однією його частиною, учні легко зро­зуміють, якщо пов'язати цю операцію із знаходженням однієї час­тини числа.

Найдоцільніше, як установлено досвідом, використати для цього геометричні засоби конкретизації умов цих задач. Наприклад, учитель креслить на дошці відрізок 80 см завдовжки, позначає кінці його буквами АВ, а зверху записує довжину.

На пропозицію вчителя учні усно знаходять відрізка АВ, а один з учнів відкладає з лівого кінця відрізка відрізок АС = 20 см (рис. 3).

Учитель запитує, яку частину відрізка АВ становить відрі­зок АС? Як знайшли його довжину? Потім він витирає відрізок СВ, залишаючи на дошці тільки четверту частину відрізка АВ — відрізок АС. Запитавши ще раз, яку частину відрізка АВ становить відрізок АС, пропонує учням скласти задачу, в якій треба було б за довжиною відріз­ка АС знайти довжину відрізка АВ. Учні формулюють задачу: «Відрізок АС завдовжки 20 см становить четверту час­тину відрізка АВ. Якої довжини відрі­зок АВ?»

80 см Х

С С

А В А В

Х 20 см

Рис. 3

Усно діти відразу знаходять, що дов­жина відрізка АВ становить 80 см. Проте вчитель цим не задовольняється. Він вимагає обґрунтувати дію:

20 см · 4 = 80 см

(Якщо частина відрізка становить 20 см, то весь відрізок у чо­тири рази довший).

Аналогічно розв'язують задачі:

1. Піонери вирушили в туристський похід. Пройшовши четверту частину дороги, вони дізналися, що пройшли 3 км. Скільки всього кілометрів повинні пройти піонери?

Х

С

А В

3 км

Рис. 4

Для конкретизації умови задачі вчитель креслить на дошці відрізок АВ, ділить його на 4 рівні частини. Відмічає на ньому четверту частину - відрізок АС - і під ним пише 3 км. Учні мірку­ють так: якщо четверта частина дороги

становить 3 км, то всього піонери повинні пройти відстань в чотири рази більшу: 3 км · 4 = 12 км (рис. 4).

Відповідь. Піонери повинні пройти 12 км.

2. Четверту частину лікарських рослин (від кількості зібраної початковими класами) зібрали учні других класів. Скільки кіло­грамів лікарських рослин зібрали початкові класи, якщо учні дру­гих класів зібрали 8 кг?

Розв'язування.

ваги лікарських рослин становить 8 кг, отже, вся їх вага становить

8 кг · 4 = 32 кг.

В і д п о в і д ь. Здали лікарських рослин 32 кг.