28.Типы точек покоя

Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем

(1)

Причём

Точка  , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).

Для исследования точки покоя системы (1) надо составить характеристическое уравнение

(2)

и найти его корни   и  .

Возможны следующие случаи.

1. Корни   характеристического уравнения (2) вещественные и разные:

а)  . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);

б)  . Точка покоя неустойчива (неустойчивый узел, рис. 33);

в)  . Точка покоя неустойчива (седло, рис. 34).

2. Корни характеристического уравнения (2) комплексные: 

а)  . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);

б)  . Точка покоя неустойчива (неустойчивый фокус, рис.36);

в)  . Точка покоя устойчива (центр, рис. 37).

3. Корни   кратные:

а)  . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);

б)  . Точка покоя неустойчива (неустойчивый узел, рис.40, 41).

Теорема. Если все корни характеристического уравнения для системы (6) имеют отрицательную вещественную часть, то точка покоя системы (6)   , асимптотически устойчива. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то точка покоя неустойчива.

29.Числовой ряд сумма ряда

ЧИСЛОВОЙ РЯД – бесконечная сумма членов бесконечной числовой последовательности {an} называется числовым рядом:

a1 + a2+ a3 + … + an+ … =  .

Каждому натуральному n сопоставляется сумма первых n членов последовательности {an}

S1 = a1, S2= a1 + a2, …, Sn = = a1 + a2 + a3 + … + an, …

Значения Sn называют частичными суммами ряда. Они образуют последовательность {Sn} последовательность частичных сумм (бесконечного) ряда an – общий член ряда.

Если последовательность частичных сумм данного ряда имеет предел S,то есть

,

то ряд сходится и S – его сумма. Записывается это следующим образом:

a1 + a2 + a3 + … + an + … = S, или  = S.

В противном случае ряд называют расходящимся.

Таким образом, сумма ряда – это, по определению, предел последовательности его частичных сумм.

Пусть есть геометрическая прогрессия bn = b1qn–1, знаменатель которой qпо абсолютной величине меньше единицы (–1 < q < 1). Вычислим сумму первых n членов геометрической прогрессии:

Sn= b1+ b1qn + b1q2 + …+ b1qn–1=  .

Очевидно, что при |q| < 1 с ростом n значение qn стремится к нулю. Тогда значение Sn стремится к   и это число называется суммой всех членов бесконечной убывающей геометрической прогрессии: b1 + b1qn + b1q2 + …= .

30.Необходимые признаки сходимости ряда

Необходимый признак сходимости ряда: последовательность членов сходящегося ряда должна стремится к нулю:  .

Это условие не является достаточным, как показывает пример ряда  .

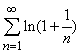Для этого ряда выполняется необходимый признак сходимости ряда:  , однако, ряд расходится, так как частичные суммы

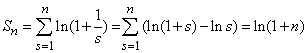неограниченно возрастают.

Для выяснения сходимости рядов найдены разнообразные достаточные признаки сходимости или расходимости рядов.

Признак Д'Аламбера: если существует такое положительное c < 1, что начиная с некоторого n, выполняется неравенство

,

то ряд сходится. Если же начиная с некоторого n, выполняется неравенство

,

то ряд расходится. Отсюда, в частности, следует сходимость геометрической прогрессии при знаменателе 0 < q < 1 и расходимость приq  1.

Признак Коши: если существует такое положительное c < 1, что, начиная с некоторого n, выполняется неравенство:

,

то ряд сходится. Если же, начиная с некоторого n, выполняется неравенство:

,

то ряд расходится.

Особое место среди рядов занимают такие, в которых знаки слагаемых строго чередуются, а абсолютные величины рядов монотонно убывают. Оказывается, для таких рядов необходимый признак сходимости ряда является одновременно и достаточным, т.е., если , то ряд   сходится.