
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
26.Приближенные метоыд решения дифференциальных уровнений
Рассмотрим задачу Коши (5.2), (5.6) для дифференциального уравнения первого порядка: найти решение уравнения y'=f(x,y), удовлетворяющее условию y(x0)=y0. Пусть y(x)- решение поставленной задачи Коши. Подставив это решение в уравнение (5.2), получим тождество y'(x) ≡ f(x,y(x)). Интегрируя это тождество по x, получаем
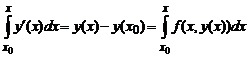 ,
,
или, что тоже самое,
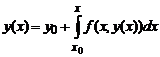 .
(5.15)
.
(5.15)
Таким образом, мы показали, что всякое решение задачи Коши (5.2), (5.6) есть решение интегрального уравнения (5.15). С другой стороны, если y(x)- решение интегрального уравнения (5.15), то дифференцируя (5.15) по x, получаем, что y(x)- решение задачи Коши (5.2), (5.6).
Решение интегрального уравнения (5.15) будем искать с помощью метода последовательных приближений. Положим
y0(x)=y0, 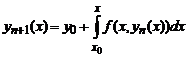 .
(5.16)
.
(5.16)
Если оператор
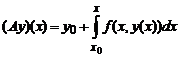 -
(5.17)
-
(5.17)
сжимающий [12], то последовательные приближения (5.16) сходятся к решению интегрального уравнения (5.15), а, следовательно и дифференциального уравнения y' = f(x,y), удовлетворяющего условию y(x0) = y0. Желающие могут познакомиться с доказательством сжимаемости оператора (5.17) в [12].
Пример. Найдём с помощью метода последовательных приближений решение уравнения y' = y, удовлетворяющее условию y(0)=1. Подставляя y(0)=1 в (5.16), получаем
y0=1, 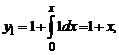
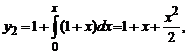 …,
…,
![]()
С другой стороны, решая исходную задачу Коши, имеем y = ex.
Таким образом, нами получено разложение функции ex в ряд Тейлора в нуле (ряд Маклорена).
Перейдём
теперь к изложению численного метода
Эйлера решения задачи Коши (5.2), (5.6).
Разобьём отрезок [a,b], на котором мы ищем
решение, на части точками x0 =
a<x1<…<xn =
b. Положим yi=y(xi),
hi =
xi+1 -
xi,
0≤i≤n. Так как по определению производной ![]() то
заменяя производную y'(xi)
конечной разностью
то
заменяя производную y'(xi)
конечной разностью ![]()
![]() в
уравнении (5.2), получаем
в
уравнении (5.2), получаем ![]() ,
или, что то же самое,
,
или, что то же самое,
yi+1 = yi + h·f(xi, yi), (5.17)
Соотношение (5.17) является расчётной формулой метода Эйлера численного решения задачи Коши (5.2), (5.6). Вычислив yi , i = 0,1,..,n получим таблицу значений решения в точках xi , i = 0,1,..,n Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение y(x) по формуле Тейлора в окрестности точки xi до членов второго порядка малости
y(xi+1)=y(xi+h)=y(xi)+y'(xi)h+o(h2)=yi+hf(xi,yi)+o(h2).
Сравнивая с (5.17) видим, что погрешность формулы (5.17) равна o(h2). К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например методом прогноза и коррекции [14], либо другими методами, в частности методом Рунге-Кутта [14].
27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
Рассмотрим систему дифференциальных уравнений
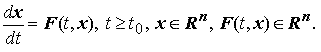
Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши.Пусть некоторое фиксированное решение x = φ(t) этой системы существует при всех t ≥ t0. Решение x = φ(t) системы называется асимптотически устойчивым по Ляпунову при t ≥ t0 , если :
— решение x = φ(t) устойчиво по Ляпунову при t ≥ t0 ;
— существует такое число Δ > 0, что любое решение x = φ(t), удовлетворяющее условию | x(t0) − φ(t0) | < Δ с ростом t стремится к нулю: | x(t0) − φ(t0) | → 0 при t → ∞. .
Геометрически это означает, что интегральные кривые x = x(t), близкие в момент t = t0 к интегральной кривой x = φ(t), приближаются к ней с ростом t.
Интегральные кривые и фазовые траектории, отвечающие асимптотически устойчивым решениям, тоже называются асимптотически устойчивыми.
На рисунке чёрным изображена асимптотически устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.3, 0), и две, начинающиеся вблизи неё, траектории.
