
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
20.Неоднородные линейные уравнения высших порядков
21.Системы ду. Нормальная система
Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:
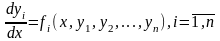 (1.1)
(1.1)
где
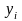 ,
,
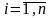 – неизвестные функции от независимой
переменной x, подлежащие определению;
– неизвестные функции от независимой
переменной x, подлежащие определению;
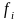 ,
– известные функции от
,
– известные функции от
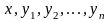 ,
заданные и непрерывные в некоторой
области. Число n называется порядком
системы (1.1). В дальнейшем ограничимся
рассмотрением систем второго порядка
(n=2).
,
заданные и непрерывные в некоторой
области. Число n называется порядком
системы (1.1). В дальнейшем ограничимся
рассмотрением систем второго порядка
(n=2).
Определение 2. Пусть дана нормальная система уравнений
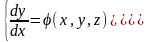 (1.2)
(1.2)
где
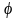 и
и
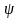 – заданные и непрерывные в некоторой
области функции. Пара функции (y(x); z(x)),
определенная на (a,b), имеющая непрерывные
производные и удовлетворяющая на (a,b)
обоим уравнениям системы (1.2), называется
ее решением.
– заданные и непрерывные в некоторой
области функции. Пара функции (y(x); z(x)),
определенная на (a,b), имеющая непрерывные
производные и удовлетворяющая на (a,b)
обоим уравнениям системы (1.2), называется
ее решением.
Задача
нахождения решения (y(x); z(x)), удовлетворяющего
начальным условиям
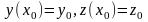 ,
где
,
где
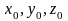 – заданные числа (начальные данные),
называется задачей Коши.
– заданные числа (начальные данные),
называется задачей Коши.
22.Геометрический смысл решения системы ду
23.Интегрирование систем ду
Системы дифференциальных уравнений n–го порядка можно решать сведением к уравнению n–го порядка. Такой метод решения систем называетсяметодом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
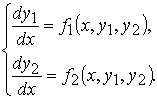
Исключим функцию y2. Для этого сначала выразим y2 через x и y1 из первого уравнения системы , затем продифференцируем по x первое уравнение системы, заменяя y2 полученным для него выражением, а производную y2 − правой частью второго уравнения системы:
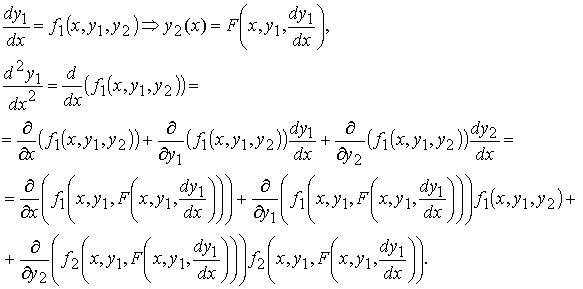
Получили обыкновенное дифференциальное уравнение 2 –го порядка
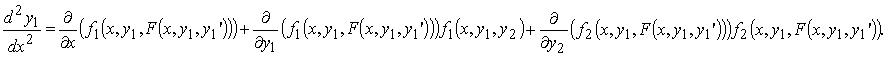
Таким же образом решают методом исключения произвольные системы n–го порядка: дифференцируют уравнения системы и, последовательно исключая функции y2, ..., yn и их производные, сводят систему к одному дифференциальному уравнению n–го порядка относительно y1.
24.Системы ду с постоянными коэффициентами
ЛОС ДУ с постоянными коэффициентами.
Эта система имеет вид
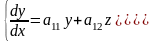 (4.1)
(4.1)
где
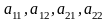 - постоянные. Система (4.1) имеет
фундаментальную систему решений,
состоящую из элементарных функций.
Основным методом построения фундаментальной
системы решений (4.1) является метод
Эйлера. Согласно этому методу, решение
ЛОС ДУ ищется в виде
- постоянные. Система (4.1) имеет
фундаментальную систему решений,
состоящую из элементарных функций.
Основным методом построения фундаментальной
системы решений (4.1) является метод
Эйлера. Согласно этому методу, решение
ЛОС ДУ ищется в виде
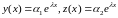
Дифференцируем обе функции по x и подставляем в (4.1):
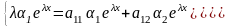
Сокращаем
оба уравнения системы на
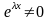 :
:
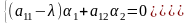 (4.2)
(4.2)
Так
как
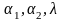 - некоторые постоянные числа, подлежащие
определению, среди которых хотя бы одно
отлично от нуля, то определитель системы
(4.2) должен быть равен нулю
- некоторые постоянные числа, подлежащие
определению, среди которых хотя бы одно
отлично от нуля, то определитель системы
(4.2) должен быть равен нулю
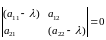 (4.3)
(4.3)
Уравнение (4.3) называется характеристическим уравнением, а его корни – характеристическими числами системы (4.1). Каждому из корней характеристического уравнения соответствует хотя бы одно частное решение указанного выше вида. Различают три случая.
Оба
корня характеристического уравнения
вещественны и различны:
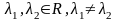 .
Подставляем
.
Подставляем
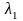 в одно из уравнений системы (4.2), например,
в первое уравнение:
в одно из уравнений системы (4.2), например,
в первое уравнение: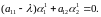 Из него с точностью до константы
определяем
Из него с точностью до константы
определяем
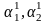 ,
откуда получаем первое решение ЛОС ДУ:
,
откуда получаем первое решение ЛОС ДУ:
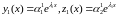 .
То же самое проделываем со вторым корнем
характеристического уравнения
.
То же самое проделываем со вторым корнем
характеристического уравнения
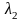 и в результате получаем второе, линейно
независимое на
и в результате получаем второе, линейно
независимое на
![]() ,
решение ЛОС ДУ:
,
решение ЛОС ДУ:
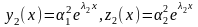 .
Следовательно, согласно теореме 2 §3
общим решением системы (4.1) будет следующее
семейство функций:
.
Следовательно, согласно теореме 2 §3
общим решением системы (4.1) будет следующее
семейство функций:
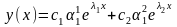
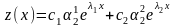 .
.
2.
Если
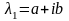 - корень характеристического уравнения,
то
- корень характеристического уравнения,
то
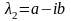 .
Подставляем
в одно из двух уравнений системы (4.2) и
с точностью до постоянной получаем
.
Теперь можно составить первое решение
системы (4.1):
.
Подставляем
в одно из двух уравнений системы (4.2) и
с точностью до постоянной получаем
.
Теперь можно составить первое решение
системы (4.1):
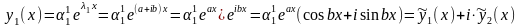
 .
.
Отделив вещественную и мнимую части, получим два вещественных линейно независимых частных решения системы (4.1), соответствующих корню a+ib. Решения, соответствующие корню a-ib, будут линейно зависимы с решениями, соответствующими крню a+ib.
Итак, общее решение ЛОС ДУ в этом случае имеет вид:
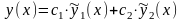
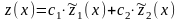 .
.
3.
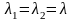
В
случае кратного корня характеристического
уравнения предлагается представить
общее решение системы уравнений (4.1) в
следующем виде:
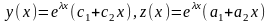 ,
где
,
где
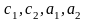 - постоянные числа, причем
- постоянные числа, причем
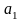 и
и
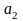 должны быть выражены через
должны быть выражены через
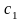 и
и
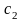 .
Рассмотрим поясняющий пример.
.
Рассмотрим поясняющий пример.
25.Решени систем ленейных ДУ высших порядков с постоянным коэффициентам
Интегрирование линейных дифференциальных уравнений связано с понятием линейной независимости функций. Функции у1, у2, .... yn называются линейно зависимыми в данном интервале изменения аргумента х, если в этом интервале выполняется тождество C1y1+C2y2+…+Cnyn=0, где C1, C2, ..., Сn - постоянные, из которых хоть одна отлична от нуля. Если же в данном интервале изменения х указанное тождество выполняется только тогда, когда все постоянные С1, С2, ..., Сn равны нулю, то функции у1, у2, ..., yn называются линейно независимыми в данном интервале.
Необходимое условие линейной зависимости функции: если функции у1, у2, ..., уn линейно зависимы в данном интервале изменения аргумента, то определитель Вронского (вронскиан)
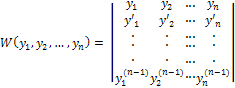
тождественно равен нулю в этом интервале. Отсюда: если W(y1, y2, ..., yn)≠0, то функции линейно независимы в этом интервале (достаточное условие линейной независимости функций).
Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами а0, a1, ..., an:
![]()
Общее решение имеет вид
![]()
здесь С1, С2, …, Сn - произвольные постоянные; у1, y2, …, yn - линейно независимые решения соответствующего однородного уравнения (система таких решений называется фундаментальной); у* - какое-либо частное решение данного неоднородного уравнения.
Для отыскания у1, у2, ..., уn следует найти корня характеристического уравнения:
![]()
Простому
действительному корню rm соответствует
решение однородного уравнения ![]()
Действительному корню rm кратности k соответствуют решения
![]()
Если
rm=α+iβ (комплексный корень), то имеется
и сопряженный корень ![]() ;
этой паре корней соответствуют
;
этой паре корней соответствуют
![]()
Если rm=α+iβ - комплексный корень кратности k, то имеется и сопряженный корень той же кратности k; этой паре корней соответствуют решения
![]()
![]()
![]()
ПРИМЕР 1. Уравнение изгиба балки на упругом основании
![]()
Характеристическое
уравнение k4+b4=0 имеет корни ![]()
отсюда получаем
![]()
![]()
Общее решение однородного уравнения
![]()
Для нахождения частного решения у* неоднородного уравнения либо применяют способ неопределенных коэффициентов, если правая часть имеет структуру, указанную выше (см. 1.9.4), либо пользуются вариацией произвольных постоянных. При этом в общем случае частное решение у* ищут в форме
![]()
Производные С′i(х) определяют из системы алгебраических линейных уравнений, определитель которой есть определитель Вронского, отличный от нуля в силу линейной независимости решений y1, у2, ..., уn:
![]()
![]()
![]()
![]()
![]()
имея C′i(x) находят интегрированием Сi(х).
Наряду с методом вариации произвольных постоянных применяется «символический метод» [1.11.1].
