
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
11.Ду высших порядков. Общее и частное решение
Основные понятия
Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям. Уравнение вида
![]()
где bo(x) ≠ 0, b1(x),..., bn(x), g(x) - заданные функции (от х), называется линейным ДУ n-го порядка.
Оно содержит искомую функцию у и все ее производные лишь в первой степени. Функции bo(x), b1(x),..., bn(x) называются коэффициентами уравнения (3.11), а функция g(x) - его свободным членом.
Если свободный член g(x)=0, то уравнение (3.11) называется линейным однородным уравнением; если g(x) ≠ 0, то уравнение (3.11) называется неоднородным.
Разделив уравнение (3.11) на bo(x) ≠ 0 и обозначив
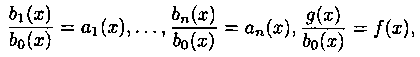
запишем уравнение (3.11) в виде приведенного:
![]()
Далее будем рассматривать линейные ДУ вида (3.12) и считать, что коэффициенты и свободный член уравнения (3.12) являются непрерывными функциями (на некотором интервале (а;b)). При этих условиях справедлива теорема существования и единственности решения ДУ (3.12) (см. теорему. 3.1).
12.Уравнение
вида
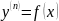
Найти
общий интеграл этого уравнения.
Проинтегрируем по х все части, принимая
во внимание
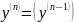

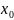 -любое
фиксированное значение
-любое
фиксированное значение
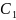 -постоянная
интегрирований получаем:
-постоянная
интегрирований получаем:
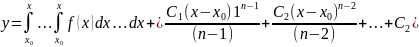
Чтобы найти часное решение, удовлетв начальному условиям, достаточно положить:
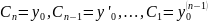
13.Некоторые типы ДУ приводящие к уравнениям первого порядка
14.Линейное однородное уравнение. Свойства. Определитель Вронского
15.Формула Лиувиля
Теорема
14.5.6.1. Определитель Вронского системы
y1(x), y2(x), …, yn(x) решений однородного
уравнения удовлетворяет уравнению
![]() где p1(x) - коэффициент при n - 1 производной.
где p1(x) - коэффициент при n - 1 производной.
Док-во.
Докажем эту теорему для уравнения
второго порядка
![]() Пусть y1(x), y2(x) - частные решения этого
уравнения, тогда ,
Пусть y1(x), y2(x) - частные решения этого
уравнения, тогда ,
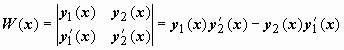 .
.
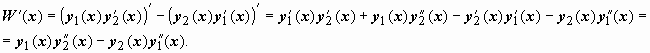 Так как y1(x), y2(x) - решения уравнения, то
,
Так как y1(x), y2(x) - решения уравнения, то
,
![]()
![]() . Умножим
первое из этих уравнений на - y2(x), второе
- на y1(x) и сложим:
. Умножим
первое из этих уравнений на - y2(x), второе
- на y1(x) и сложим:
![]()
В первой из квадратных скобок стоит W(x), во второй - , поэтому , что и требовалось доказать.
Для
доказательства этой теоремы в общей
случае надо знать правило дифференцирования
функциональных определителей: производная
определителя n-го порядка равна сумме
n определителей, которые получаются из
исходного определителя построчным
дифференцированием. Для определителя
Вронского

так
как первые n - 1 определитель содержат
равные строки и равны нулю. Каждая из
функций y1(x), y2(x), …, yn(x) удовлетворяет
уравнению
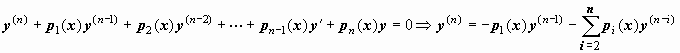 поэтому, поставив эти выражения в
последнюю строку и пользуясь свойствами
определителей, получим
поэтому, поставив эти выражения в
последнюю строку и пользуясь свойствами
определителей, получим
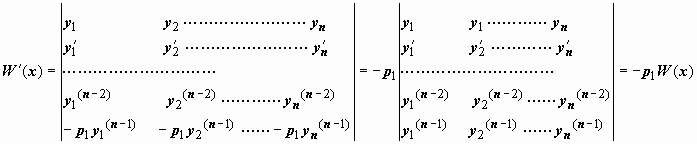
т.е.
![]() .
.
Решим
это уравнение относительно W(x). Функция
W(x) = 0 является решением этого уравнения;
если
![]() то
то
![]() Интегрируем последнее выражение в
пределах от x0 до x:
Интегрируем последнее выражение в
пределах от x0 до x:
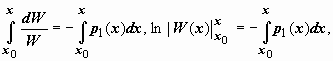
 (Мы отбросили знак модуля у дроби, так
как W(x) - непрерывная функция, не
обращающаяся в нуль, поэтому значения
W(x) и W(x0) всегда имеют один знак).
Окончательно .
(Мы отбросили знак модуля у дроби, так
как W(x) - непрерывная функция, не
обращающаяся в нуль, поэтому значения
W(x) и W(x0) всегда имеют один знак).
Окончательно .
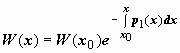 (28)
(28)
Формула
(28)называется формулой Лиувилля. Из неё
также следуют результаты предыдущих
разделов: если W(x0) = 0, то
![]() ;
если
;
если
![]() , то
ни в одной точке интервала (a, b).
, то
ни в одной точке интервала (a, b).
