
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
6.Однородное уравнение первого порядка
Функция
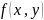 -
однородная функция п-го порядка
относительно переменных х и у, если при
любой ƛ справедливо тождество:
-
однородная функция п-го порядка
относительно переменных х и у, если при
любой ƛ справедливо тождество:
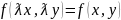
Уравнение первого порядка:
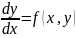 -
называется
однородным относительно х,у если функция
f(x,y)
является однородной функцией неравного
измерения относительно х и у
-
называется
однородным относительно х,у если функция
f(x,y)
является однородной функцией неравного
измерения относительно х и у
Решение однородного уравенения:
По условию
Теперь
возьмем
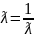 .
Получается
.
Получается
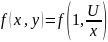
Уравнение в этом случае примет вид:
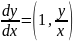
Сделаем
подстановку: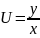
y=Ux, тогда
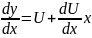
Подставив в (2) получим:
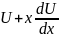 =f(1,U)
=f(1,U)
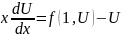
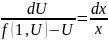
Интегрируя находим:
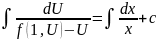
Подставляя вместо U его значение получим интеграл уравнения
7.Линейные однородные ду. Решение уравнения
Функция
![]() называется однородной функцией своих
аргументов измерения
называется однородной функцией своих
аргументов измерения
![]() , если справедливо тождество .
, если справедливо тождество .
![]()
Например,
функция
![]() есть однородная функция второго
измерения, так как
есть однородная функция второго
измерения, так как
![]()
При
![]() имеем функцию нулевого измерения.
Например,
имеем функцию нулевого измерения.
Например,
![]() есть однородная функция нулевого
измерения, так как
есть однородная функция нулевого
измерения, так как
![]()
Дифференциальное
уравнение вида
![]() называется однородным относительно х
и у , если
есть однородная функция своих аргументов
нулевого измерения. Однородное уравнение
всегда можно представить в виде
называется однородным относительно х
и у , если
есть однородная функция своих аргументов
нулевого измерения. Однородное уравнение
всегда можно представить в виде
![]() (1)
(1)
Вводя
новую искомую функцию
![]() , уравнение (1) можно привести к уравнению
с разделяющими переменными:
, уравнение (1) можно привести к уравнению
с разделяющими переменными:
![]()
Если
![]() есть корень уравнения
есть корень уравнения
![]() , то решение однородного уравнения будет
или
, то решение однородного уравнения будет
или
![]() (прямая, проходящая через начало
координат).
(прямая, проходящая через начало
координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .
8.Уравнение Бернулли
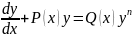
Здесь Р(х) и Q(x) непрерывная функция от х, а п≠0≠ 1
Это
уравнение можно привести к линейному
сдел преоброзованием разделив его на
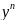
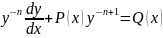
Делаем
замену: z=
Получим
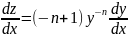
Подставим данное уравнение в 1е и получим:
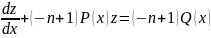
Получили линейное уравнение
9.Уравнение в полных дифференциалах
Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N – две заданные функции, то его можно представить как M(x,y)dx – N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d(y2 – x2) = 0. Функция F(x,y) в этом случае равна (1/2)(y2 – x2); некоторые из ее линий постоянного уровня представлены на рис. 1.
10. Особые решения ду 1 порядка
Особые
точки и особые решения уравнения первого
порядка.
Если в окрестности точки (x0,
y0)
плоскости для уравнения
![]() выполняются
условия существования и единственности
решения задачи Коши (непрерывность f(x,
y)
и
выполняются
условия существования и единственности
решения задачи Коши (непрерывность f(x,
y)
и
![]() ),
то через эту точку проходит единственная
интегральная кривая. Если эти условия
нарушаются, точку (x0,
y0)
называют особой
точкой
дифференциального уравнения. Через
особую точку может не проходить ни одной
и
),
то через эту точку проходит единственная
интегральная кривая. Если эти условия
нарушаются, точку (x0,
y0)
называют особой
точкой
дифференциального уравнения. Через
особую точку может не проходить ни одной
и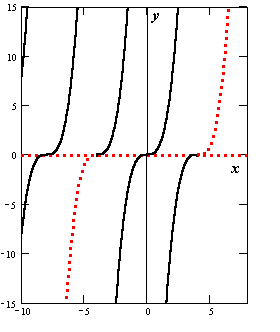 нтегральной
кривой (т.е. задача
,
y(x0)
= y0
не имеет решения); может проходить одна
интегральная кривая; может проходить
несколько интегральных кривых. Особые
точки могут образовать кривую, которая
сама является интегральной кривой
уравнения. Решение уравнения, в каждой
точке которого нарушается его
единственность, называют особым
решением.
Для примера рассмотрим уравнение
нтегральной
кривой (т.е. задача
,
y(x0)
= y0
не имеет решения); может проходить одна
интегральная кривая; может проходить
несколько интегральных кривых. Особые
точки могут образовать кривую, которая
сама является интегральной кривой
уравнения. Решение уравнения, в каждой
точке которого нарушается его
единственность, называют особым
решением.
Для примера рассмотрим уравнение
![]() .
Здесь
.
Здесь
![]() -
непрерывна в любой точке (x,
y),
но
-
непрерывна в любой точке (x,
y),
но
![]() -
не имеет конечного предела при
-
не имеет конечного предела при
![]() ,
т.е. в любой точке (x,
y)
при y
= 0 нарушается условие существования
непрерывной производной
,
т.е. в любой точке (x,
y)
при y
= 0 нарушается условие существования
непрерывной производной
![]() .
Следовательно, любая точка (x,
0) является особой точкой уравнения.
Прямая y
= 0, очевидно, интегральная кривая
уравнения (функция y
= 0 удовлетворяет уравнению). Найдём
общее решение этого уравнения:
.
Следовательно, любая точка (x,
0) является особой точкой уравнения.
Прямая y
= 0, очевидно, интегральная кривая
уравнения (функция y
= 0 удовлетворяет уравнению). Найдём
общее решение этого уравнения:
![]() .
Несколько таких функций приведено на
рисунке справа вверху вместе с решением
y
= 0. В любой точке (x,
0) нарушается единственность решения,
таким образом, решение y
= 0 - особое. На самом деле через любую
точку (x,
0)проходит бесконечное количество
интегральных кривых, так как любая
кривая, составленная из частей особого
и неособых решений (одна такая кривая
выделена красным пунктиром), также
является интегральной кривой.
.
Несколько таких функций приведено на
рисунке справа вверху вместе с решением
y
= 0. В любой точке (x,
0) нарушается единственность решения,
таким образом, решение y
= 0 - особое. На самом деле через любую
точку (x,
0)проходит бесконечное количество
интегральных кривых, так как любая
кривая, составленная из частей особого
и неособых решений (одна такая кривая
выделена красным пунктиром), также
является интегральной кривой.
