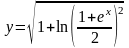- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
4.Ду первого порядка. Общее и частное решение
Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
![]()
где
функции P(t,x) и Q(t,x)
определены и непрерывны в некоторой
области
![]()
Уравнения в полных дифференциалах
Если
в уравнении (1) левая часть представляет
собой полный дифференциал, то есть
![]() ,
то такое уравнение называется уравнением
в полных дифференциалах
(частный случай так называемого пфаффова
уравнения).
Интегральные кривые такого уравнения
суть линии уровней функции
,
то такое уравнение называется уравнением
в полных дифференциалах
(частный случай так называемого пфаффова
уравнения).
Интегральные кривые такого уравнения
суть линии уровней функции
![]() ,
т.е. определяются уравнением
,
т.е. определяются уравнением
![]() при
всевозможных значениях произвольной
постоянной
при
всевозможных значениях произвольной
постоянной
![]() .
.
Если
в области
![]() выполнено
условие
выполнено
условие
![]() ,
то общее решение уравнения (1) определяется
из уравнения
как
неявная функция
,
то общее решение уравнения (1) определяется
из уравнения
как
неявная функция
![]() .
Через каждую точку области
проходит
единственная интегральная кривая
уравнения
(1).
.
Через каждую точку области
проходит
единственная интегральная кривая
уравнения
(1).
Если
рассматриваемая область
односвязна,
а производные
![]() также
непрерывны в
,
то для того, чтобы (1) было уравнением в
полных дифференциалах, необходимо и
достаточно выполнения условия
также
непрерывны в
,
то для того, чтобы (1) было уравнением в
полных дифференциалах, необходимо и
достаточно выполнения условия
![]()
Частным
решением
уравнения (1) на интервале (a,
b)
(конечном или бесконечном) называется
любая n
раз дифференцируемая функция
![]() ,
удовлетворяющая этому уравнению, т.е.
обращающая уравнение на этом интервале
в тождество.
,
удовлетворяющая этому уравнению, т.е.
обращающая уравнение на этом интервале
в тождество.
![]() Так,
функция y(x)
= ex
+ x
обращает уравнение : y(4)
– y
+ x
= 0 в тождество на всей числовой оси
(y(4)(x)
= ex;
ex
–(ex
+x)
+ x
= 0), т.е. является частным решением этого
уравнения. Любое уравнение порядка
Так,
функция y(x)
= ex
+ x
обращает уравнение : y(4)
– y
+ x
= 0 в тождество на всей числовой оси
(y(4)(x)
= ex;
ex
–(ex
+x)
+ x
= 0), т.е. является частным решением этого
уравнения. Любое уравнение порядка
![]() имеет
множество частных решений (частным
решением приведённого уравнения является
и функция y(x)
= sin(x)
+ x).
Процедуру решения дифференциального
уравнения часто называют интегрированием
уравнения, при этом интегрировать
приходится в общем случае ровно n
раз, и при каждом интегрировании в
решение входит очередная произвольная
постоянная.
Опр.
Общим решением (общим интегралом)
уравнения
(1) называется такое соотношение
имеет
множество частных решений (частным
решением приведённого уравнения является
и функция y(x)
= sin(x)
+ x).
Процедуру решения дифференциального
уравнения часто называют интегрированием
уравнения, при этом интегрировать
приходится в общем случае ровно n
раз, и при каждом интегрировании в
решение входит очередная произвольная
постоянная.
Опр.
Общим решением (общим интегралом)
уравнения
(1) называется такое соотношение
|
(2) |
что:
1. Любое решение (2)
![]() относительно
y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) - частное решение уравнения
(1);
2.
Любое частное решение уравнения (1) может
быть получено из (2) при некотором наборе
постоянных C1,
C2,
…, Cn.
Мы
будем в основном рассматривать
дифференциальные уравнения в форме,
разрешённой относительно старшей
производной:
относительно
y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) - частное решение уравнения
(1);
2.
Любое частное решение уравнения (1) может
быть получено из (2) при некотором наборе
постоянных C1,
C2,
…, Cn.
Мы
будем в основном рассматривать
дифференциальные уравнения в форме,
разрешённой относительно старшей
производной:
|
(3) |
и получать общее решение в форме
; |
(4) |
решённой относительно неизвестной функции.
5.Уравнение с разделенними и разделяющимися переменными
1.Уравнения
вида
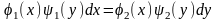 ,
в котором коэффициенты при дифференциалах
распадаются на множители, зависящие
только от X
и только от Y
называется уравнением с разделяющими
переменными.
Путём деления на произведение
,
в котором коэффициенты при дифференциалах
распадаются на множители, зависящие
только от X
и только от Y
называется уравнением с разделяющими
переменными.
Путём деления на произведение
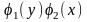 оно приводится к уравнению с разделёнными
переменными:
оно приводится к уравнению с разделёнными
переменными:
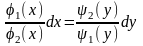
Общий интеграл этого уравнения имеет вид
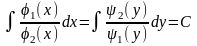
Пример
2.1. Найти частное решение уравнения
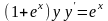 ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию
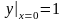
Решение.
Имеем
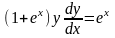
Разделяя переменные, получаем
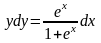
Интегрируя, найдём общий интеграл
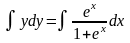
 (1)
(1)
Полагая
X=0
и Y=1,
будем иметь
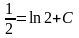 ,
откуда
,
откуда
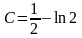
Подставляя
в (1) найденное значение C,
получаем частное решение
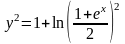 ;
;
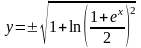
Из
начального
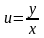 условия следует, что
условия следует, что
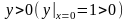 поэтому перед корнем берём знак плюс.
Итак, искомое частное решение
поэтому перед корнем берём знак плюс.
Итак, искомое частное решение