
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
66.Свойства преобразований по Лапласу
Функцией-оригиналом называется комплекснозначная функция f (t) действительного аргумента t, удовлетворяющая условиям:
1. f (t) интегрируема на любом конечном интервале оси t;
2. f (t)=0 для всех отрицательных t;
3. f (t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М и 0, что |f(t)|<Me0t для всех t.
Изображением функции f (t) (по Лапласу) называется функция F(p) комплексного переменного p= +i , определяемая равенством
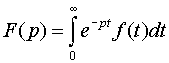 .
.
Тот факт, что F(p) есть изображение f (t), будем символически записывать так:
![]() .
.
Для любой функции-оригинала f (t) изображение определено в полуплоскости Rep>0 и является в этой полуплоскости аналитической функцией.
Из определения изображения следуют его простейшие свойства:
1. Линейность. Для любых комплексных постоянных a и b
![]()
(здесь и далее считать f(t)=F(p), g(t)=G(p)).
2.Теорема подобия. Для любого постоянного a >0
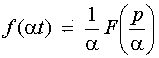 .
.
3. Дифференцирование оригинала. Если функции f (t), f(t) , f (t),…, f (n)(t) являются функциями-оригиналами и f(t)=F(p), то
![]() ,
,
![]() ,
,
![]() ,
,
где
под f (k)(0),
(k= 1, 2,…, n-1) понимается ![]() .
.
4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала
![]()
или вообще
![]() .
.
5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то
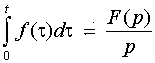 .
.
6. Интегрирование
изображения. Если интеграл 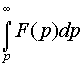 сходится,
то он служит изображением функции
сходится,
то он служит изображением функции![]()
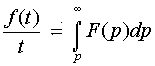 .
.
7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р0
![]() .
.
8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0
![]() .
.
Важной для приложений является следующая:
Теорема единственности
Если две функции (t) и (t) имеют одно и то же L-изображение F(p), то эти функции тождественно равны.
67.Теорема о свертке
Определение.
Сверткой функций f1(t) и f2(t) называется
функция 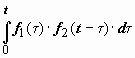 .
Свёртка
обозначается символом f1 * f2:
.
Свёртка
обозначается символом f1 * f2: 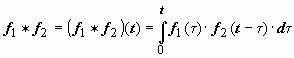 .
Если f1(t) и f2(t) -
функции-оригиналы, то их свёртка - тоже
функция-оригинал, показатель роста
которой превышает наибольший из
показателей роста функций f1(t) и f2(t) не
больше, чем на 1. Действительно,
пусть
.
Если f1(t) и f2(t) -
функции-оригиналы, то их свёртка - тоже
функция-оригинал, показатель роста
которой превышает наибольший из
показателей роста функций f1(t) и f2(t) не
больше, чем на 1. Действительно,
пусть ![]() ,
, ![]() ,
, ![]() ,
тогда
,
тогда 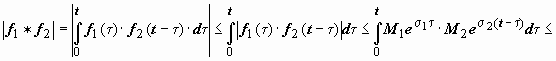
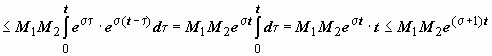 ,
так как t < e t.
Свёртка
функций коммутативна: f (t)
* g (t)
= g (t)
* f (t),
в этом легко убедиться, заменив в
интеграле
переменную τ на τ1 = t −τ.
Можно
показать, что свёртка обладает свойством
ассоциативности, т.е. что ( f1 * f2 )
* f3 = f1 *
( f2 * f3 ).
,
так как t < e t.
Свёртка
функций коммутативна: f (t)
* g (t)
= g (t)
* f (t),
в этом легко убедиться, заменив в
интеграле
переменную τ на τ1 = t −τ.
Можно
показать, что свёртка обладает свойством
ассоциативности, т.е. что ( f1 * f2 )
* f3 = f1 *
( f2 * f3 ).
68.Нахождение оригинала по изображению
Для решения задачи о нахождении оригинала f (t) по известному изображению F(p) применяются следующие приемы, используемые при выполнении задания 31:
Применение теоремы умножения.
Пример 1. 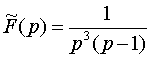 .
.
Решение. Пусть
![]() ,
,
где 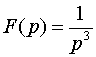 ,
а
,
а 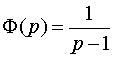 .
.
По таблице определяем оригиналы функций F(р) и Ф(р):
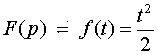 ,
,
![]() .
.
Искомый
оригинал ![]() определяем
как свертку оригиналов f (t) и (t)
определяем
как свертку оригиналов f (t) и (t)
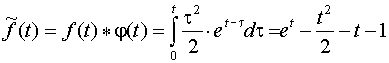 .
.
2. Применение формулы Дюамеля. Если функция-оригинал f (t) непрерывна на [0,+ ), а функция-оригинал (t) непрерывно дифференцируема на [0, ) и
![]() ,
, ![]() ,
,
то
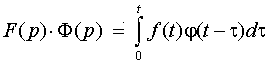 .
.
Отсюда по теореме о дифференцировании оригинала
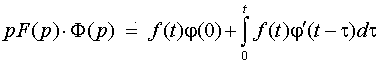 .
.
Это – так называемая формула Дюамеля.
Пример
2. 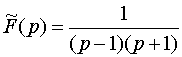 .
.
Решение. Обозначим искомый оригинал через , т. е.
![]() .
.
Пусть 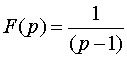 ,
а
,
а 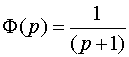 .
.
Тогда ![]() ,
а
,
а ![]() .
.
Находим ![]() ,
, ![]() и
по формуле Дюамеля имеем
и
по формуле Дюамеля имеем
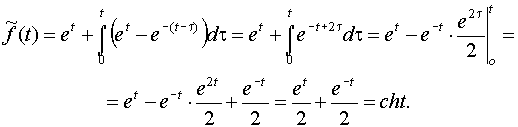
Если 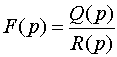
есть правильная рациональная дробь, то разлагают эту дробь на сумму простых дробей и находят оригинал для каждой простой дроби, используя свойства преобразования Лапласа.
Пример 3. 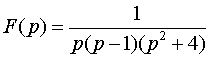 .
.
Решение. Разлагаем F(p) в сумму простых дробей:
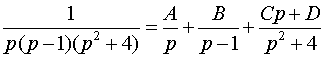 .
.
Находя коэффициенты А, В, С, D, получаем
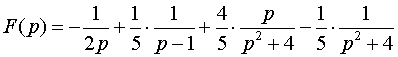 .
.
С помощью таблицы определяем
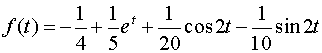 .
.
Ответ: 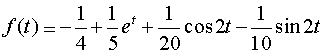 .
.
4. Применение второй теоремы разложения. Вторая теорема разложения утверждает, что при определенных условиях на F(p) оригиналом для F(p) служит функция
![]() ,
,
где сумма вычетов берется по всем особым точкам рk функции F(p).
В частности, если
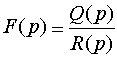
правильная рациональная дробь, то оригиналом ее служит функция
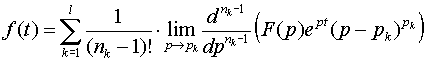 ,
(1)
,
(1)
где рk – полюсы F(p) кратности nk и сумма берется по всем полюсам F(p).
Пример
4. 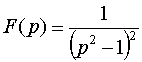 .
.
Решение. Функция F(p) имеет полюс p1=1 и p2=-1каждый второго порядка. В формуле (1) n1=2, n2=2, l=2, k=1, 2.
По формуле (1) имеем
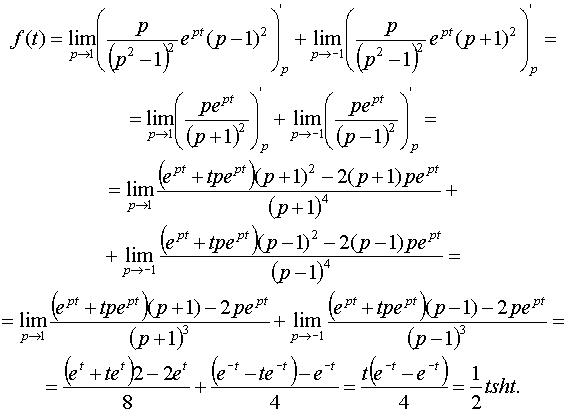
Если все полюсы функции F(p) простые, то формула из п.4 упрощается и принимает вид
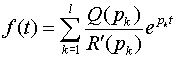 .
.
Пример
5.
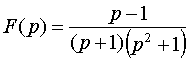 .
.
Решение. Имеем случай, когда все полюса F(p) простые:
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,

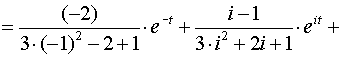
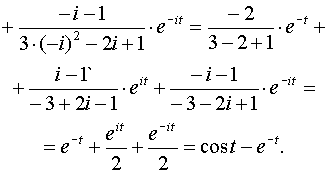
Еслu
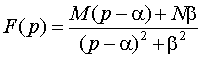 ,
,
то
![]()
. Пример
6. 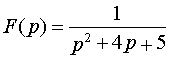 .
.
Решение. Поскольку
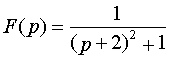 ,
,
то ![]() .
.
Имеем
![]() .
.
