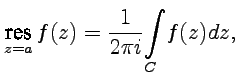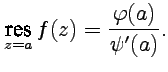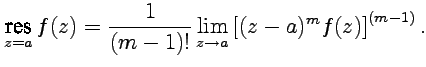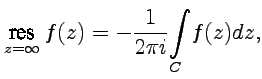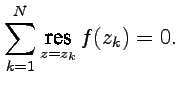- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
57.Степенные ряды. Ряд Тейлора и Маклорена.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
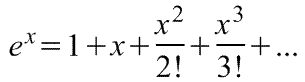
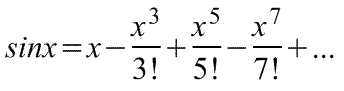
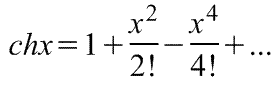
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:
1)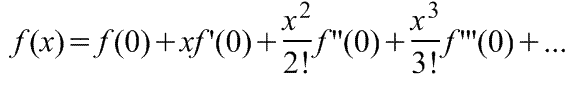 ,
где f(x) - функция, имеющая при а=0 производные
всех порядков. Rn -
остаточный член в ряде Маклорена
(=Макларена) (Тейлора при а=0)определяется
выражением
,
где f(x) - функция, имеющая при а=0 производные
всех порядков. Rn -
остаточный член в ряде Маклорена
(=Макларена) (Тейлора при а=0)определяется
выражением 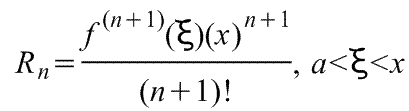
2)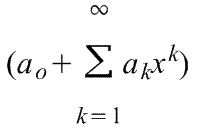
k-тый коэффициент (при хk) ряда определяется формулой
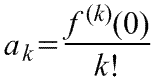
Ряды Маклорена являются частным случаем рядов Тейлора.
Ряд
Тейлора. Пусть
функция w = f(z) аналитична
в области D, z0∈ D.
Обозначим L окружность
с центром в z0,
принадлежащую области D вместе
с ограниченным ею кругом. Тогда для
любой точки z,
лежащей внутри L, ![]() .
Представим множитель
.
Представим множитель ![]() в
виде суммы сходящейся геометрической
прогрессии:
(так
как | z – z0|
< | t – z0| ,
то
)
,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать:
в
виде суммы сходящейся геометрической
прогрессии:
(так
как | z – z0|
< | t – z0| ,
то
)
,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать: 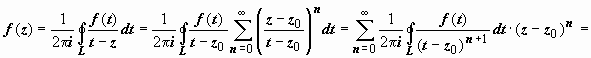
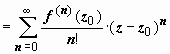 ,
так как
,
так как 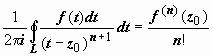 .
Итак,
.
Итак, 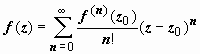 .
Ряд
в правой части этого равенства - ряд
Тейлора функции f(z).
Этот ряд абсолютно сходится внутри
контура L,
а в качестве L можно
взять любую окружность, которая не
выходит за пределы областиD.
Доказана
Теорема
о разложении функции в ряд Тейлора. Если
функция w = f(z) аналитична
в области D, z0 ∈ D,
то функция f(z)может
быть разложена в ряд Тейлора по
степеням (z – z0)n.
Этот ряд абсолютно сходится к f(z) внутри
круга | z – z0|
< r,
где r -
расстояние от z0 до
границы области D (до
ближайшей к z0 точке,
в которой функция теряет аналитичность).
Это разложение единственно.
Единственность
разложения следует из того, что
коэффициенты ряда однозначно выражаются
через производные функции.
.
Ряд
в правой части этого равенства - ряд
Тейлора функции f(z).
Этот ряд абсолютно сходится внутри
контура L,
а в качестве L можно
взять любую окружность, которая не
выходит за пределы областиD.
Доказана
Теорема
о разложении функции в ряд Тейлора. Если
функция w = f(z) аналитична
в области D, z0 ∈ D,
то функция f(z)может
быть разложена в ряд Тейлора по
степеням (z – z0)n.
Этот ряд абсолютно сходится к f(z) внутри
круга | z – z0|
< r,
где r -
расстояние от z0 до
границы области D (до
ближайшей к z0 точке,
в которой функция теряет аналитичность).
Это разложение единственно.
Единственность
разложения следует из того, что
коэффициенты ряда однозначно выражаются
через производные функции.
59.Классификация изолированных особых точек однозначной функции
точка а![]() Сz называется изолированной
особой точкой однозначного
характера функции f (z),
если f (z)
аналитическая и однозначная (регулярная)
в кольце {z:0<|z–a|< },
а в самой точке ане
определена.
Сz называется изолированной
особой точкой однозначного
характера функции f (z),
если f (z)
аналитическая и однозначная (регулярная)
в кольце {z:0<|z–a|< },
а в самой точке ане
определена.
Бесконечно
удаленная точка называется изолированной
особой точкой однозначного
характера функции f (z),
если f (z)
регулярна в некоторой окрестности
{R<|z|<![]() }
точки z=
и
функция
}
точки z=
и
функция 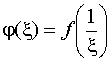
имеет в точке =0 изолированную особую точку однозначного характера.
В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.
Изолированная особая точка а функции f (z) называется
а) устранимой особой точкой, если существует конечный предел
![]()
б) полюсом, если
![]()
в) существенно особой точкой, если
![]()
не существует.
Заметим, что типы особых точек z= функции f (z) и =0 функции совпадают, ибо
![]()
Пусть
функция f (z)
регулярна в точке а (и,
следовательно, в некоторой окрестности
этой точки). Число т, т![]() 1,
называется кратностью (или порядком) нуля
функции f (z)
в точке а,
если выполнены условия
1,
называется кратностью (или порядком) нуля
функции f (z)
в точке а,
если выполнены условия
f (a)=f (a)=…=f (m-1)(a)=0,
f (m)(a)![]() 0.
0.
При т=1 точка а называется простым нулем функции f (z), при m>1-кратным.
Порядком (или кратностью) полюса функции g(z) в точке а называется кратность нуля в точке а регулярной функции
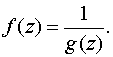
Если а – простой нуль f (z), то точка а называется простым полюсом функции g(z).
Замечание.
Вообще, если
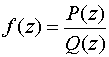 ,
где P(z) и Q(z)
– полиномы, не имеющие общих корней, то
корни полинома Q(z)
(и только они) являются полюсами
функции f (z).
,
где P(z) и Q(z)
– полиномы, не имеющие общих корней, то
корни полинома Q(z)
(и только они) являются полюсами
функции f (z).
Порядок полюса f (z) совпадает с кратностью соответствующих корней полинома Q(z).
Точка z= называется нулем кратности m 1 для функции f (z), регулярной в этой точке, если функция
имеет нуль кратности т в точке =0.
Если z=а – изолированная особая точка однозначного характера для функции f (z), то f (z) регулярна в некотором кольце {z: 0<|z-a|<r} и ее можно разложить в ряд Лорана, сходящийся в этом кольце,
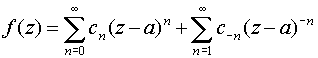 .
.
Тип изолированной особой точки однозначного характера определяется видом лорановского разложения функции в проколотой окрестности этой точки.
1. Для того чтобы точка а была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы лорановское разложение этой функции в окрестности точки а не содержало главной части.
2. Для того чтобы точка а была полюсом функции f (z), необходимо и достаточно, чтобы главная часть лорановского разложения функции f (z) в окрестности этой точки содержала лишь конечное число членов (причем полюсом порядка т 1, если главная часть имеет вид
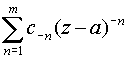 ,
где ст
0.
,
где ст
0.
3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f (z) в окрестности этой точки содержит бесконечно много отличных от нуля членов.
Разложение
функции f (z)
в окрестности бесконечно удаленной
точки в ряд Лорана имеет вид 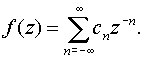
Здесь роль главной части играют члены с положительными степенями z, а члены с отрицательными степенями образуют правильную часть.
Опираясь на приведенные критерии типа особой точки и определение вычета в точке z= , рекомендуем читателю сформулировать соответствующие утверждения для точки z= .
60.Вычеты и их приложения
Вычетом
функции
в
изолированной точке ![]() называется
интеграл
называется
интеграл
|
(66) |
где ![]() -
замкнутый контур, содержащий одну особую
точку
. Эквивалентное
определение вычета можно получить,
сравнивая (66)
с выражением для коэффициентов ряда
Лорана (61),
тогда вычетом функции
называется
значение коэффициента
-
замкнутый контур, содержащий одну особую
точку
. Эквивалентное
определение вычета можно получить,
сравнивая (66)
с выражением для коэффициентов ряда
Лорана (61),
тогда вычетом функции
называется
значение коэффициента ![]() ряда
Лорана в окрестности точки
:
ряда
Лорана в окрестности точки
:
|
(67) |
Из
определений вычета следует, что если
-
правильная точка функции
,
то ![]() .
Если точка
является
полюсом, то удобно рассмотреть отдельные
случаи:
.
Если точка
является
полюсом, то удобно рассмотреть отдельные
случаи:
-полюс первого порядка:
|
(68) |
так
как в случае полюса первого порядка
функция может быть представлена в
виде 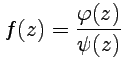 ,
причем
-
ноль первого порядка функции
,
причем
-
ноль первого порядка функции ![]() ,
то
,
то
|
(69) |
-полюс
порядка ![]() :
:
|
(70) |
Вычетом
функции
в
точке ![]() называется
интеграл
называется
интеграл
|
(71) |
причем
во внешней части контура
функция
не
имеет особых точек, находящихся на
конечном расстоянии от ![]() .
Эквивалентно, с помощью коэффициентов
ряда Лорана в окрестности бесконечности,
.
Эквивалентно, с помощью коэффициентов
ряда Лорана в окрестности бесконечности, 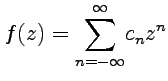 .
.
|
(72) |
На
основе этих определений можно показать,
что имеет место следующая теорема:если
функция
является
аналитической на полной комплексной
плоскости, за исключением конечного
числа особых точек (включая бесконечную) ![]() ,
тогда
,
тогда
|
(73) |