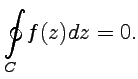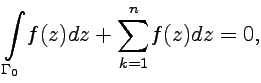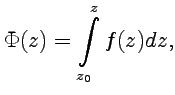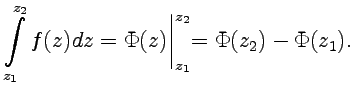- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
55.Интеграл по комплексному переменному
Пусть ![]() -
непрерывная функция комплексного
-
непрерывная функция комплексного ![]() ,
определенная в области
,
определенная в области ![]() и
и ![]() -
гладкая кривая, лежащая в
,
с началом в точке
-
гладкая кривая, лежащая в
,
с началом в точке ![]() и
концом в точке
и
концом в точке ![]() (рис.
137), заданная уравнением
(рис.
137), заданная уравнением
![]()
![]()
или, что все равно, двумя уравнениями
![]() .
(1)
.
(1)
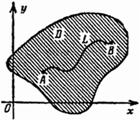
Рис. 137
Как
всегда, направление на
соответствует
изменению параметра ![]() от
от ![]() до
до ![]()
![]() .
.
Интеграл
от функции ![]() вдоль
кривой
определяется
следующим образом:
вдоль
кривой
определяется
следующим образом:
![]()
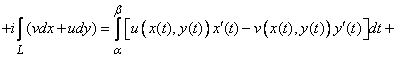
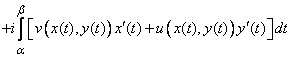 .
.
Если
учесть, что ![]() и
и ![]() ,
то равенство (2) можно коротко записать
так:
,
то равенство (2) можно коротко записать
так:
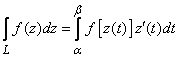 .
(3)
.
(3)
Таким образом, из (2) видно, что интеграл по комплексному переменному есть сумма двух криволинейных интегралов, и его вычисление сводится к вычислению обыкновенных интегралов.
Интеграл
(2) существует для любой непрерывной
функции
(в
этом случае функции ![]() и
и ![]() также
непрерывны) и любой гладкой кривой
(т.
е. когда
также
непрерывны) и любой гладкой кривой
(т.
е. когда ![]() ,
, ![]() )
непрерывны и
)
непрерывны и ![]() ).
).
Если
кривая
кусочно-гладкая
и состоит из гладких ориентированных
кусков ![]() ,
то по определению считаем
,
то по определению считаем
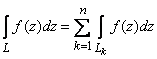 .
(4)
.
(4)
На основании свойств криволинейного интеграла легко получаем
1)
![]() ,
,
где ![]() та
же кривая, что и
,
но ориентированная противоположно (см.
нашу книгу «Высшая математика.
Дифференциальное и интегральное
исчисление», § 7.4).
та
же кривая, что и
,
но ориентированная противоположно (см.
нашу книгу «Высшая математика.
Дифференциальное и интегральное
исчисление», § 7.4).
2)
![]() ,
,
где ![]() -
постоянные числа.
-
постоянные числа.
3)
Если ![]() при
при ![]() ,
то
,
то
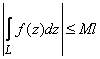 ,
,
где ![]() -
длина
.
-
длина
.
В самом деле, на основании свойства обыкновенного интеграла имеем
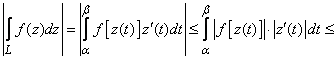
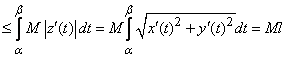 .
.
56.Теорема Коши. Интеграл Коши
Результат,
полученный в примере 3-5,
является частным случаем теоремы Коши
и, если ![]() является
аналитической (или только дифференцируемой)
функцией в области
является
аналитической (или только дифференцируемой)
функцией в области ![]() комплексной
плоскости, то интеграл по любой замкнутой
кривой
комплексной
плоскости, то интеграл по любой замкнутой
кривой ![]() от
равен
нулю:
от
равен
нулю:
|
(48) |
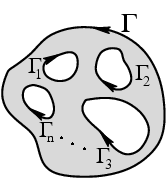
Теорема Коши имеет несколько важных следствий:
|
|
|
|
|
(49) |
|
|
Рис.17 |
|
||
|
|
|
|
где
все участки границы обходятся в
положительном направлении, т. е. когда
захватываемая область остается слева
при движении вдоль каждой кривой ![]() ;
значение
интеграла
;
значение
интеграла ![]() от
функции
по
некоторой кривой, соединяющей точки
от
функции
по
некоторой кривой, соединяющей точки ![]() и
и ![]() ,
т. е.:
,
т. е.:
|
(50) |
будет
аналитической функцией переменной
,
причем ![]() . Функция
(50)
называется первообразной,
и для нее имеет место комплексный аналог
формулы Ньютона-Лейбница:
. Функция
(50)
называется первообразной,
и для нее имеет место комплексный аналог
формулы Ньютона-Лейбница:
|
(51) |
58.Ряд Лорана
Ряд
Лорана. Пусть
функция f(z) аналитична
в кольце ρ ≤ |z − z0|
≤ R.
Тогда для любой точки этого кольца 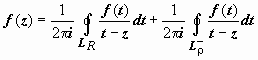 ;
при этом окружности проходятся так, что
область остаётся слева (следствие 3
раздела 19.7.2.
Интегральная формула Коши). Изменим в
интеграле по внутренней окружности
направление обхода на противоположное:
;
при этом окружности проходятся так, что
область остаётся слева (следствие 3
раздела 19.7.2.
Интегральная формула Коши). Изменим в
интеграле по внутренней окружности
направление обхода на противоположное: 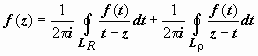 .
Интеграл по внешней окружности преобразуем
так, как и при выводе формулы Тейлора:
.
Интеграл по внешней окружности преобразуем
так, как и при выводе формулы Тейлора: 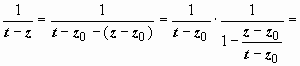 (так
как | z – z0|
< | t – z0| ,
то
(так
как | z – z0|
< | t – z0| ,
то ![]() )
) 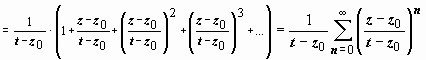 ,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать:
,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать: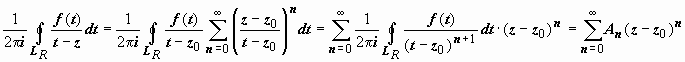 ,
где
,
где 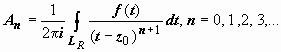 .
Интеграл по внутренней окружности
преобразуем аналогично, учитывая только,
что на Lρ | t – z0|
< | z – z0| :
.
Интеграл по внутренней окружности
преобразуем аналогично, учитывая только,
что на Lρ | t – z0|
< | z – z0| : 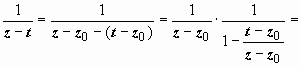
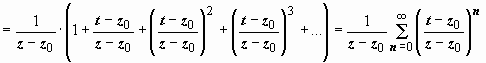 .
И здесь ряд сходится абсолютно, поэтому
его можно почленно интегрировать:
.
И здесь ряд сходится абсолютно, поэтому
его можно почленно интегрировать: 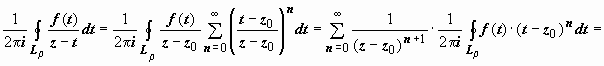
 ,г
,г де
де 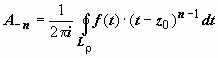 .
Переобозначим n →
−n, тогда форма коэффициентов ряда
для Lρ совпадёт
с формой коэффициентов ряда для LR:
.
Переобозначим n →
−n, тогда форма коэффициентов ряда
для Lρ совпадёт
с формой коэффициентов ряда для LR: 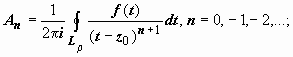 поэтому
окончательно для интеграла по Lρ получим
поэтому
окончательно для интеграла по Lρ получим 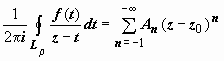 .
Докажем, что и контур для вычисления
коэффициентов может быть взят один и
тот же. Действительно, пусть Γ -
кусочно-гладкий контур, расположенный
в кольце ρ ≤ |z − z0|
≤ R,
и точка z0 расположена
внутри этого контура. По теореме Коши
для многосвязной области
.
Докажем, что и контур для вычисления
коэффициентов может быть взят один и
тот же. Действительно, пусть Γ -
кусочно-гладкий контур, расположенный
в кольце ρ ≤ |z − z0|
≤ R,
и точка z0 расположена
внутри этого контура. По теореме Коши
для многосвязной области 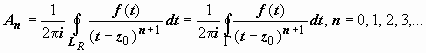 ;
; 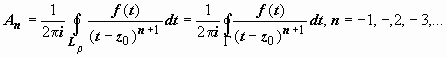 ,
поэтому для любого n
,
поэтому для любого n ![]() ,
и
,
и
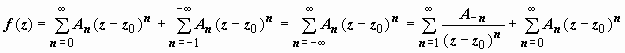 .
Этот
ряд (содержащий и положительные, и
отрицательные степени (z – z0),
называется рядом Лорана функции f(z).
Его часть, содержащая неотрицательные
степени (
.
Этот
ряд (содержащий и положительные, и
отрицательные степени (z – z0),
называется рядом Лорана функции f(z).
Его часть, содержащая неотрицательные
степени (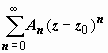 ),
называется правильной; часть, содержащая
отрицательные степени (
),
называется правильной; часть, содержащая
отрицательные степени (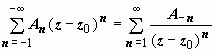 ), называется
главной. Правильная часть, по самому
своему построению, сходится в
круге | z – z0|
≤ R,
главная - во внешности круга | z – z0|
≥ ρ, поэтому весь ряд сходится в
пересечении этих областей, т.е. в кольце
ρ ≤ | z – z0|
≤ R.
Так же, как и для ряда Тейлора, разложение
в ряд Лорана единственно.
Еще
раз подчеркнем, что в ряд Лорана
раскладывается функция, аналитическая
в кольце, и ширина этого кольца определяется
областью аналитичности функции, т.е.
разложение теряет смысл там, где
функция теряет аналитичность. Рассмотрим
), называется
главной. Правильная часть, по самому
своему построению, сходится в
круге | z – z0|
≤ R,
главная - во внешности круга | z – z0|
≥ ρ, поэтому весь ряд сходится в
пересечении этих областей, т.е. в кольце
ρ ≤ | z – z0|
≤ R.
Так же, как и для ряда Тейлора, разложение
в ряд Лорана единственно.
Еще
раз подчеркнем, что в ряд Лорана
раскладывается функция, аналитическая
в кольце, и ширина этого кольца определяется
областью аналитичности функции, т.е.
разложение теряет смысл там, где
функция теряет аналитичность. Рассмотрим