52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.

Производная функции комплексного переменного определяется, как и производная в действительной области: Здесь z0, z _  комплексные и f(z0) = f(z0+z) - f(z).

Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.

1. Сумма и произведение дифференцируемых в точке функций,  есть функция и справедливы равенства:

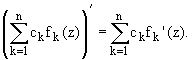
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :

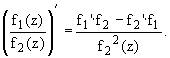
3. Сложная функция f( (z)) дифференцируема в точке z0, если в этой точке дифференцируема функция  (z), а функция f(u) дифференцируема в точке u0, где u0 =  (z0) и u =  (z). При этом в точке z0 имеет место формула:

Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.  Например, рассмотрим функцию  f(z) = z3. По определению производной для любой точки z, принадлежащей комплексной области, записываем:

Предел существует для любой точки z, принадлежащей комплексной области и (z3)' =3z2. Аналогично можно получить: (zn)' = nzn-1 (n - действительное число).

 

ПРИМЕР 1. Вычисление значения производной функции коплексного переменного в точке.

 

Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),  то справедливы следующие утверждения:

1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей u(x, y) = Re f(z),   v(x, y) = Im f(z)  и выполняется условие Коши-Римана:

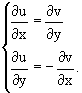
2. Если u(x, y)  и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция   f(z) = f(x+iy) = u(x, y) + iv(x, y)  дифференцируема в точке z0 = x0+ iy0.

3. Производная дифференцируемой функции может быть записана по одной из формул:

     

53. Условие Коши-Римана

Теорема (необходимые условия дифференцирования). Пусть функция   дифференцируема в точке  . Тогда функции   имеют частные производные в точке   удовлетворяют следующим условиям:

.

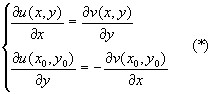
Условия (*) называются условиями Коши-Римана.

Доказательство.

Пусть  . Какую бы не выбрали траекторию   отношение   будет стремится к одному и тому же числу.

Выберем 2 траектории.

    (действительная ось)     (мнимая ось)

  .

  .

Сравнивая вещественные и мнимые части первого и второго уравнения получаем условие Коши-Римана.

Пример.

54.Конформные отображения

Взаимно однозначное отображение области D на область D* (евклидова пространства или риманова многообразия) называется конформным (лат. conformis — подобный), если в окрестности любой точки D дифференциал этого преобразования есть композиция ортогонального преобразования и гомотетии.

Этот термин пришёл из комплексного анализа, изначально использовался только для конформных отображений областей плоскости.

Связанные определения

Если при конформном отображении сохраняется ориентация, то говорят о конформном отображении первого рода; если же она меняется на противоположную, то говорят о конформном отображении второго рода либо антиконформном отображении .

Две метрики   на гладком многообразии M называются конформноэквивалентными если существует гладкая функция   такая что  . В этом случае тождественное отображение на M индуцирует конформное отображение  .

Свойства

Конформное отображение сохраняет форму бесконечно малых фигур;

Конформное отображение сохраняет углы между кривыми в точках их пересечения (свойство сохранения углов).

Это свойство можно также взять за определение конформного отображения.

Теорема Лиувилля: Всякое конформное отображение области евклидова пространства   при   можно представить в виде конечного числа суперпозиций — изометрий и инверсий.

Кривизна Вейля сохраняется при конформном отображении, то есть если   и g — конформноэквивалентные метрические тензоры, то      где   и W обозначают тензоры Вейля для   и g соответственно.

Для конформно-эквивалентых метрик 

Связности связаны следующей формулой:    

Кривизны связаны следующей формулой:           если g(X,X) = g(Y,Y) = 1,g(X,Y) = 0,Xψ = 0 а Hessψ обозначает Гессиан функции ψ.

Формулу для секционных кривизн можно записать в следующем виде:      где f = e − ψ.

При вычислении скалярной кривизны n-мерного риманова многообразия, удобнее записывать конформный фактор в виде  . В этом случае: