
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
40. Интервал и радиус сходимости степенного ряда
В
соответствии с теремой Абеля отметим:
при условии, что![]() является
точкой сходимости ряда (30.2) ряд предполагает
сходимость абсолютно во всех точках
интервала
является
точкой сходимости ряда (30.2) ряд предполагает
сходимость абсолютно во всех точках
интервала![]() Если
Если![]() есть
точка расходимости (30.2), то во всех точках
интервалов
есть
точка расходимости (30.2), то во всех точках
интервалов![]() ряд
расходится. Тогда заключим: имеется
такое число
ряд
расходится. Тогда заключим: имеется
такое число![]() ,
что на
,
что на![]() ряд
(30.2) сходится абсолютно, а на
ряд
(30.2) сходится абсолютно, а на![]() расходится.
В этом случае справедлива нижеобозначенная
теорема.
расходится.
В этом случае справедлива нижеобозначенная
теорема.
Т: Область сходимости ряда (30.2) — это интервал предполагается расходимость ряда.
Интервал
определен
в качестве его радиуса сходимости.
Существуют некоторые ряды, для которых
интервал сходимости вырождается в
точку![]() ,
при этом, имеются и такие ряды, для
которых интервал охватывает всю ось
,
при этом, имеются и такие ряды, для
которых интервал охватывает всю ось![]() .
Если
.
Если![]() ,
то ряд может расходиться и сходиться.
Это зависит от конкретного ряда.
,
то ряд может расходиться и сходиться.
Это зависит от конкретного ряда.
Запишем
способ нахождения радиуса сходимости
ряда (30.2). Исследуем ряд, составленный
их абсолютных величин его членов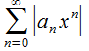 и
используем по отношению к нему признак
Даламбера:
и
используем по отношению к нему признак
Даламбера:

При
условии, что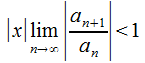 (иначе
выражаясь,
(иначе
выражаясь,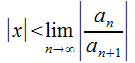 )
ряд из абсолютных величин членов (30.2)
сходится и ряд (30.2) сходится абсолютно.
Запишем
)
ряд из абсолютных величин членов (30.2)
сходится и ряд (30.2) сходится абсолютно.
Запишем
(30.4)
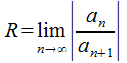
Если![]() ,
то ряд (30.2) расходится, поскольку общий
член ряда
,
то ряд (30.2) расходится, поскольку общий
член ряда![]() не
стремится к
не
стремится к![]() Получается,
что формула (30.4) обеспечивает радиус
сходимости.
Получается,
что формула (30.4) обеспечивает радиус
сходимости.
Пример: Определить радиус и интервал сходимости ряда
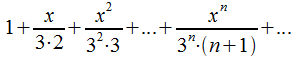
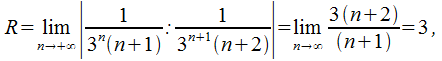
интервал
абсолютной сходимости![]() На
концах интеграла: если
На
концах интеграла: если![]() ,
то
,
то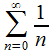 представляет
собой гармонический расходящийся ряд,
в случае же когда
представляет
собой гармонический расходящийся ряд,
в случае же когда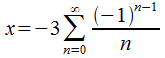 —
это знакочередующийся ряд, который
предполагает условную сходимость.
Промежуток
—
это знакочередующийся ряд, который
предполагает условную сходимость.
Промежуток![]() есть
область сходимости обозначенного ряда.
есть
область сходимости обозначенного ряда.
Ряд
(30.1) можно свести к ряду (30.2) посредством
осуществления замены переменной![]()
Если
ряд
,
то ряд (30.1) сходится абсолютно для![]() ,
иначе выражаясь, сходимость имеется на
интервале
,
иначе выражаясь, сходимость имеется на
интервале![]()
41. Действие над степенными рядами (свойства степенных рядов)
Свойства степенных рядов

Рассмотрим степенной ряд
с0 + с1 х + с2 х2 + ... + сn xn + ... , (10.1)
имеющий
радиус сходимости R>0 (R может равняться ![]() ).
Тогда каждому значению х из интервала
сходимости соответствует некоторая
сумма ряда. Следовательно, сумма
степенного ряда есть функция от х на
интервале сходимости. Обозначим ее
через S(x). Тогда можно записать равенство
).
Тогда каждому значению х из интервала
сходимости соответствует некоторая
сумма ряда. Следовательно, сумма
степенного ряда есть функция от х на
интервале сходимости. Обозначим ее
через S(x). Тогда можно записать равенство
S(x) = c0 + c1 x + c2 x2 + ... + cn xn + ... , (10.2)
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции S(x) в этой точке. В этом же смысле будем говорить, что ряд (10.1) сходится к функции S(x) на интервале сходимости. Вне интервала сходимости равенство (10.2) не имеет смысла.
Для степенных рядов справедливы следующие утверждения:
Теорема 1.
Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S(n)(x).
Теорема 2.
Степенной
ряд можно неограниченное число раз
почленно интегрировать в пределах от
0 до х, если х ![]() (-R;
R), причем получающиеся при этом степенные
ряды имеют тот же радиус сходимости,
что и исходный ряд, а суммы их соответственно
равны
(-R;
R), причем получающиеся при этом степенные
ряды имеют тот же радиус сходимости,
что и исходный ряд, а суммы их соответственно
равны 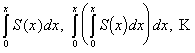 .
.
