
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
31.Сравнение рядов с положительными членами
О п р е д е л е н и е. Ряды с положительными членами – это ряды, члены которых не отрицательны. Например, для ряда (2) это означает
![]() (10)
(10)
Некоторые авторы называют ряды с положительными членами положительными рядами.
Признак Даламбера. Если для ряда
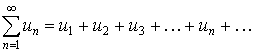 (11)
(11)
существует предел
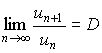 ,
(12)
,
(12)
то ряд (11) сходится, если D<1 и расходится, если D>1.
Признак Коши. Если для ряда
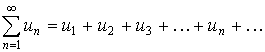 (13)
(13)
существует предел
![]() ,
(14)
,
(14)
то ряд (13) сходится, если c<1, и расходится, если c>1.
Интегральный признак Маклорена – Коши. Этот признак построен на идее сравнения ряда с несобственным интегралом. Представим ряд с положительными членами в виде
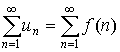 ,
(15)
,
(15)
где f (n)
= un -
значение некоторой функции f(x)
при x = n,
определенной в области x ![]() 1.
1.
Если f(x) при x 1 непрерывная, положительная и монотонно убывающая функция, то ряд (15) сходится или расходится в зависимости от того, сходится или расходится интеграл
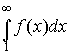 ,
,
т.е. существует конечный предел
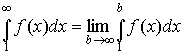 .
(16)
.
(16)
Первый признак сравнения. Пусть даны два ряда с положительными членами
(17) и
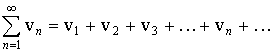 (18)
(18)
и
каждый член ряда (17) не превосходит
соответствующего члена ряда (18), т.е.
выполняется ![]() (n =
1, 2, 3, …). Тогда, если сходится ряд (18), то
сходится и ряд (17). Если ряд (17) расходится,
то ряд (18) также расходится. Этот признак
остается в силе, если условие
выполняется
не для всех n,
а лишь начиная с некоторого номера n = N.
(n =
1, 2, 3, …). Тогда, если сходится ряд (18), то
сходится и ряд (17). Если ряд (17) расходится,
то ряд (18) также расходится. Этот признак
остается в силе, если условие
выполняется
не для всех n,
а лишь начиная с некоторого номера n = N.
Второй признак сравнения. Если существует конечный отличный от нуля предел
![]() ,
,
то
оба ряда с положительными членами
![]() и
и ![]()
одновременно сходятся или одновременно расходятся.При использовании этих признаков исследуемый ряд часто сравнивается или с бесконечной геометрической прогрессией
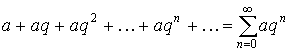 , q >
0, (19)
, q >
0, (19)
которая при q < 1 сходится и имеет сумму S = a / (1-q), а при q 1 расходится, или с расходящимся гармоническим рядом
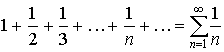 .
(20)
.
(20)
32.Признаки сравнения. Признак Даламбера.
(Признак Даламбера) Допустим, что строго положительный ряд (29) таков, что существует (конечный или бесконечный) предел
![]()
![]() (30)
(30)
Тогда при l > 1 ряд (28) расходится, а при l < 1 сходится.
Допустим
сначала, что l >
1. Так как дробь ![]() стремится
к l,
то достаточно далекие значения этой
дроби будут удовлетворять неравенству
стремится
к l,
то достаточно далекие значения этой
дроби будут удовлетворять неравенству
![]()
![]() (31)
(31)
Пусть, например, это неравенство выполнено для всех n, удовлетворяющих неравенству n > m. Тогда ряд
am+1 + am+2 + am+3 + ... (32)
таков, что у него отношение уже любого последующего члена к своему предыдущему оказывается удовлетворяющим неравенству (31). Значит (по лемме 1), ряд (32) расходится, а так как это есть остаток ряда (28), то этот последний ряд также расходится.
Пусть
теперь l <
1. Закрепим какое-нибудь число q,
удовлетворяющее неравенству l < q <
1 (например, положим ![]() ).
Тогда найдется такое m,
что при всехn > m будет
).
Тогда найдется такое m,
что при всехn > m будет
![]()
Снова составляя ряд (32) и применяя к нему лемму 2, убеждаемся сначала в сходимости ряда (32), а затем и ряда (28).
Доказанная
теорема действительно имеет совершенно
алгорифмический характер: для ее
применения надо лишь составить
отношение ![]() и
изучить его поведение при безгранично
возрастающем n.
Никаких вспомагательных рядов для
сопоставления с данным рядом искать
уже не требуется. Надо заметить, однако,
что теорема 3 применима далеко не всегда.
Не говоря уже о том, что предела (30) может
не существовать, этот предел может
равняться 1, и тогда теорема также не
позволяет сделать никакого заключения
относительно сходимости ряда.
и
изучить его поведение при безгранично
возрастающем n.
Никаких вспомагательных рядов для
сопоставления с данным рядом искать
уже не требуется. Надо заметить, однако,
что теорема 3 применима далеко не всегда.
Не говоря уже о том, что предела (30) может
не существовать, этот предел может
равняться 1, и тогда теорема также не
позволяет сделать никакого заключения
относительно сходимости ряда.
