
- •1.Задачи, приводящие к ду
- •2.Основные понятия теории ду
- •3.Задачи Коши. Теорема существования и единственности решения
- •Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.
- •4.Ду первого порядка. Общее и частное решение
- •5.Уравнение с разделенними и разделяющимися переменными
- •6.Однородное уравнение первого порядка
- •7.Линейные однородные ду. Решение уравнения
- •8.Уравнение Бернулли
- •9.Уравнение в полных дифференциалах
- •10. Особые решения ду 1 порядка
- •11.Ду высших порядков. Общее и частное решение
- •16.Линейные ду 2го порядка с постоянными коэффицентаки
- •17.Линейное ду п-го порядка с постоянными коэффициентаки
- •18.Неоднородное линейное уравнение 2го порядка
- •19.Метод вариации производных постоянных
- •20.Неоднородные линейные уравнения высших порядков
- •21.Системы ду. Нормальная система
- •22.Геометрический смысл решения системы ду
- •23.Интегрирование систем ду
- •24.Системы ду с постоянными коэффициентами
- •26.Приближенные метоыд решения дифференциальных уровнений
- •27.Понятие устойчивости и асимптотической устойчивости по Ляпунову
- •28.Типы точек покоя
- •29.Числовой ряд сумма ряда
- •30.Необходимые признаки сходимости ряда
- •31.Сравнение рядов с положительными членами
- •32.Признаки сравнения. Признак Даламбера.
- •33. Признак сравнения. Признак коши
- •34. Интегральные сходимости знакопостоянных рядов
- •35. Знакочередующиеся ряды. Теорема Лейбница
- •36. Знакопеременный ряд абсолютная и условная сходимость
- •37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов
- •38. Мажорируемый ряд.
- •39. Степенной ряд. Теорема Абеля
- •40. Интервал и радиус сходимости степенного ряда
- •41. Действие над степенными рядами (свойства степенных рядов)
- •42. Ряды Тейлора и Маклорена.
- •45. Ряды Фурье. Вычисление коэффициентов ряда фурье
- •46. Разложение в ряд Фурье непериодической функции
- •47. Ряд фурье для четных и нечетных функций
- •48. Ряд фурье по ортогональным системам функций
- •49. Интеграл Фурье
- •50. Преобразование Фурье
- •51. Функции комплексного переменного
- •52. Дифф-ие ф-ии комплексного переменного. Аналитические функции.
- •53. Условие Коши-Римана
- •54.Конформные отображения
- •55.Интеграл по комплексному переменному
- •56.Теорема Коши. Интеграл Коши
- •58.Ряд Лорана
- •57.Степенные ряды. Ряд Тейлора и Маклорена.
- •59.Классификация изолированных особых точек однозначной функции
- •61.Вычисление вычетов
- •62.Вычет функции относительно бесконечно удаленной точки
- •63.Основная теорема о вычетах
- •64.Вычисление интегралов с помощью вычетов
- •65.Оригинал и изображение по Лапласу
- •66.Свойства преобразований по Лапласу
- •67.Теорема о свертке
- •68.Нахождение оригинала по изображению
- •69.Теоремы разложения
- •70.Операционный метод решения ду и систем ду
1.Задачи, приводящие к ду
Задача 1
Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если V(0)=100 м/с, а V(l)=50 м/с.
Решение: Примем за независимую переменную время Т, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией Т, т. е. V=V(T). Для нахождения V(T) воспользуемся вторым законом Ньютона (основным законом механики): m • a=F, где а=V'(T) - есть ускорение движущегося тела, F - результирующая сила, действующая на тело в процессе движения.
В
данном случае F=- KV2, К > 0 - коэффициент
пропорционально-сти (знак минус указывает
на то, что скорость тела уменьшается).
Следовательно, функция V=V(T) является
решением дифференциального уравнения![]() ,
Здесь m - масса тела.
,
Здесь m - масса тела.
Как
будет показано ниже (пример 2.5), где
с - const.
где
с - const.
Найдя зависимость скорости от времени, легконайти скорость точки через 3 с после начала замедления.
Найдем
сначала параметры k/m и с. Согласно условию
задачи, имеем: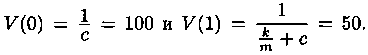 Отсюда
Отсюда![]()
Следовательно,
скорость точки изменяется по закону![]() Поэтому V(3)=25 м/с.
Поэтому V(3)=25 м/с.
Задача 2
Найти кривую, проходящую через точку (4; 1), зная, что отрезок любой касательной к ней, заключенный между осями координат, делится в точке касания пополам.
Р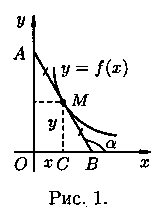 ешение:
Пусть М(х; у) - произвольная точка кривой,
уравнение которой y=ƒ(х).
Для определенности предположим, что
кривая расположена в первой четверти
(см. рис.1).
ешение:
Пусть М(х; у) - произвольная точка кривой,
уравнение которой y=ƒ(х).
Для определенности предположим, что
кривая расположена в первой четверти
(см. рис.1).
Для составления дифференциального уравнения воспользуемся геометрическим смыслом первой производной: tg а есть угловой коэффициент касательной; в точке М(х;υ) он равен y', т. е. y'=tg а.
Из
рисунка видно, что
![]() Но
Но
![]()
МС=υ. По условию задачи АМ=МВ, следовательно, ОС=СВ=х. Таким образом, получаем - tg a=у/x или y'=- у/x. Решением полученного дифференциального уравнения является функция y=4/x (гипербола). Решение будет приведено в п. 2.2 (пример 2.4).
Другие задачи
Можно показать, что:
• закон
изменения массы радия в зависимости от
времени («радиоактивный распад»)
описывается дифференциальным уравнением
![]() где
К > 0 - коэффициент пропорциональности,
м(Т) - масса радия в момент Т;
где
К > 0 - коэффициент пропорциональности,
м(Т) - масса радия в момент Т;
• «закон
охлаждения тел», т. е. закон изменения
температуры тела в зависимости от
времени, описывается уравнением![]() где
T(t) - температура тела в момент времени
t, k - коэффициент про-порциональности,
tо - температура воздуха (среды охлаждения);
где
T(t) - температура тела в момент времени
t, k - коэффициент про-порциональности,
tо - температура воздуха (среды охлаждения);
• зависимость
массы х вещества, вступившего в химическую
реакцию, от времени Т во многих случаях
описывается уравнением![]() где К - коэффициент пропорциональности;
где К - коэффициент пропорциональности;
• «закон размножения бактерий» (зависимость массы м бактерий от времени Т) описывается уравнением m't=k•m, где k > 0;
• закон
изменения давления воздуха в зависимости
от высоты над уровнем моря описывается
уравнением![]() где
р(Н) - атмосферное давление воздуха на
высоте h, k > 0.
где
р(Н) - атмосферное давление воздуха на
высоте h, k > 0.
Уже приведенные примеры указывают на исключительно важную роль дифференциальных уравнений при решении самых разнообразных задач.
