
- •11.Взаимосвязь между напряженностью и потенциалом электростатического поля.Эквипотенциальные поверхности.
- •12.Типы диэлектриков. Поляризация диэлектриков.
- •15. Проводники в электростатическом поле. Емкость уединенного проводника.
- •16. Конденсатор. Емкость конденсатора. Соединение конденсаторов в батарею.
- •27. Плазма. Термоэлектронная эмиссия. Работа выхода электрона. Электрический ток в вакууме.
- •26. Природа проводимости газов. Самостоятельный и несамостоятельный газовые разряды. Типы газовых самостоятельных разрядов и их применение.
- •28. Магнитное поле. Магнитная индукция. Принцип суперпозиции. Закон Био-Савара-Лапласа. Правило буравчика.
- •29. Расчет магнитного поля прямолинейного проводника с током. Расчет магнитного поля кругового проводника с током.
- •31. Магнитный момент витка с током. Магнитное поле движ-я электрического заряда.
- •33. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле.
- •34. Эффект Холла. Мгд-генератор. Масс-спектрограф. Циклотрон.
- •46. Намагниченность. Напряженность магнитного поля. Закон полного тока для магнитного поля в веществе.
- •45. Ферромагнетики и их свойства. Природа ферромагнетизма. Применение ферромагнетиков.
- •41. Взаимная индукция. Коэффициент взаимной индукции. Трансформатор.
- •47. Основы теории Максвелла. Вихревое электрическое поле.
- •48. Ток смещения. Опыт Эйхенвальда. Полный ток.
- •49. Уравнения Максвелла для электромагнитного поля.
- •50. Колебательные процессы. Виды колебаний. Свободные гармонические колебания и их характеристики.
- •58. Сложение перпенд-х гарм-х колебаний одинаковой частоты. Фигуры Лиссажу.
- •59. Затухающие механические колебания и их характеристики.
- •63. Вынужденные колебания в колебательном контуре. Резонанс.
- •64. Переменный электрический ток. Активное, индуктивное и емкостное сопротивление в цепи переменного тока. Закон Ома для цепи переменного тока.
- •65. Мощность в цепи переменного тока. Эффективные значения силы тока и напряжения.
- •66. Волновые процессы. Типы волн и их характеристики. Уравнение бегущей волны.
- •67. Принцип суперпозиции волн. Интерференция волн.
- •68. Стоячая волна. Уравнение стоячей волны и его анализ.
50. Колебательные процессы. Виды колебаний. Свободные гармонические колебания и их характеристики.
К![]()
![]() олебания
–
процессы в той или иной мере повторяющиеся
с течением времени. Свободные, вынужденные,
авто колебания. От фаз: механ., эл. магн.,
эл. механ. Механические колебания –
движения тел, которые повторяются точно
или приблизительно с течением времени.
Если повторение происходит через строго
равные промежутки времени, то колебания
называются периодическими.
олебания
–
процессы в той или иной мере повторяющиеся
с течением времени. Свободные, вынужденные,
авто колебания. От фаз: механ., эл. магн.,
эл. механ. Механические колебания –
движения тел, которые повторяются точно
или приблизительно с течением времени.
Если повторение происходит через строго
равные промежутки времени, то колебания
называются периодическими.
Колебательная система – система тел, которая может совершать колебательные движения. У колебательной системы есть положение равновесия – положения тел, при которых они могут находиться в покое (не совершать колебаний).
Свободные колебания – колебания, возникающие в результате внутренних сил, т. е. действующих между телами колебательной системы.
51. Дифференциальное уравнение гармонических колебаний пружинного маятника и его решение. Характеристики колебаний пружинного маятника.
П![]() ружинный
маятник –
груз, соединенный
с абсолютно упругой пружиной и совершающий
колебания под действием силы упругости
ружинный
маятник –
груз, соединенный
с абсолютно упругой пружиной и совершающий
колебания под действием силы упругости
Уравнение гармонических колебаний пружинного маятника. Период колебаний пружинного маятника.
![]() , решение уравнение
, решение уравнение
![]()
Период
происходит с собственной циклической
частотой
![]() Fупр
=
- кх
Fупр
=
- кх
52. Дифференциальное уравнение гармонических колебаний физического маятника и его решение. Характеристики колебаний физического маятника.
Физ. маятник – твердое тело, которое вращается относительно оси, не проходящей через центр тяжести. Вращение происходит под действием силы тяжести.
Ч![]() астота
астота
Период
5![]() 3.
Математический маятник. Приведенная
длина физического маятника.
3.
Математический маятник. Приведенная
длина физического маятника.
материальная точка, подвешенная на невесомой нерастяжимой нити
П![]() риведенная
длина физического маятника – длина
математического маятника, частота
колебаний которого равна частоте
колебаний рассматриваемого физического
маятника.
риведенная
длина физического маятника – длина
математического маятника, частота
колебаний которого равна частоте
колебаний рассматриваемого физического
маятника.
![]()
54. Скорость и ускорение материальной точки, совершающей гармонические колебания
55. Энергия материальной точки, совершающей гармонические колебания.
![]()
56.Гар-кие колебания в колебательном контуре. Превращения энергии в контуре.
Гармонические колебания – колебания, для которых смещение зависит от времени по закону синуса или косинуса.
57. Сложение гармонических колебаний одинаковой частоты и одинакового направления. Биения.
Биения – колебания, для которых амплитуда является медленной периодической функцией времени.
М![]() етод
векторных диаграмм
– взаимно-однозначное соответствие
между колебательным процессом и вектором,
вращающимся с постоянной угловой
скоростью: амплитуда равна длине вектора;
циклическая частота – угловой скорости;
начальная фаза – начальному углу с
горизонтальной осью; фаза – текущему
углу с горизонтальной осью; смещение –
проекции вектора на горизонтальную
ось.
етод
векторных диаграмм
– взаимно-однозначное соответствие
между колебательным процессом и вектором,
вращающимся с постоянной угловой
скоростью: амплитуда равна длине вектора;
циклическая частота – угловой скорости;
начальная фаза – начальному углу с
горизонтальной осью; фаза – текущему
углу с горизонтальной осью; смещение –
проекции вектора на горизонтальную
ось.
У![]()
![]() равнение
биений . Период биений .
равнение
биений . Период биений .
Начальная фаза и амплитуда.
![]()
![]()
58. Сложение перпенд-х гарм-х колебаний одинаковой частоты. Фигуры Лиссажу.
Уравнение траектории результирующего движения при сложении перпендикулярно направленных колебаний одной частоты
![]()
уравнение эллипса
Такие колебания эллиптически поляризованные т.к. описывает эллипс за время
![]()
Ориентация осей эллипса и их размеры зависят от амплитуд и разности фаз.
П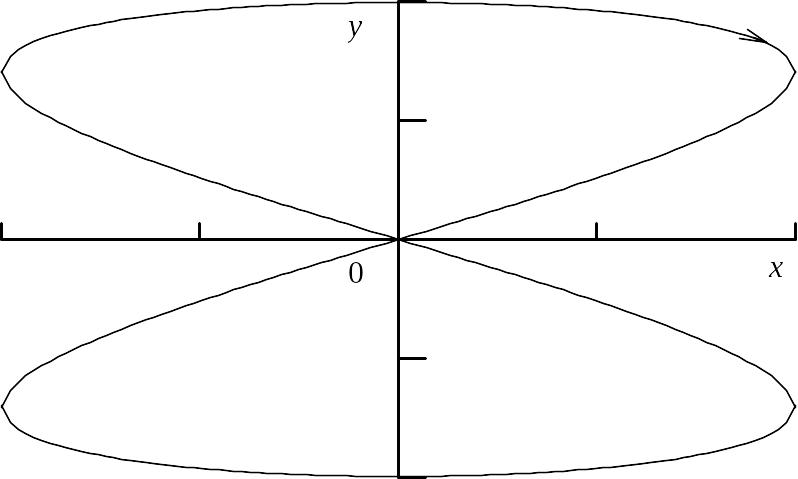 ри
А1 =
А2
– круг (колебания поляризованные по
кругу). А
=(А21+А22)1/2
– линейно
поляризованные колебания. В общем случае
траектории зависят от соотношения
частот, амплитуд и разности фаз. Это
фигуры Лиссажу.
ри
А1 =
А2
– круг (колебания поляризованные по
кругу). А
=(А21+А22)1/2
– линейно
поляризованные колебания. В общем случае
траектории зависят от соотношения
частот, амплитуд и разности фаз. Это
фигуры Лиссажу.
Фигура Лиссажу при двукратном отношении частот
